- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA SL复习笔记2.2.2 Factorising & Completing the Square
Factorising Quadratics
Why is factorising quadratics useful?
- Factorising gives roots (zeroes or solutions) of a quadratic
- It gives the x-intercepts when drawing the graph
How do I factorise a monic quadratic of the form x2 + bx + c?
- You might be able to spot the factors by inspection
- Especially if c is a prime number
- Otherwise find two numbers m and n ..
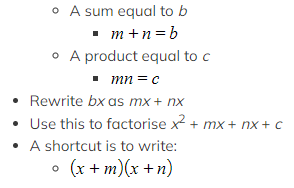 How do I factorise a non-monic quadratic of the form ax2 + bx + c?
How do I factorise a non-monic quadratic of the form ax2 + bx + c?
 How do I use the difference of two squares to factorise a quadratic of the form A2x2 - C2?
How do I use the difference of two squares to factorise a quadratic of the form A2x2 - C2?
 Exam Tip
Exam Tip
 Worked Example
Worked Example
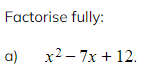

![]()
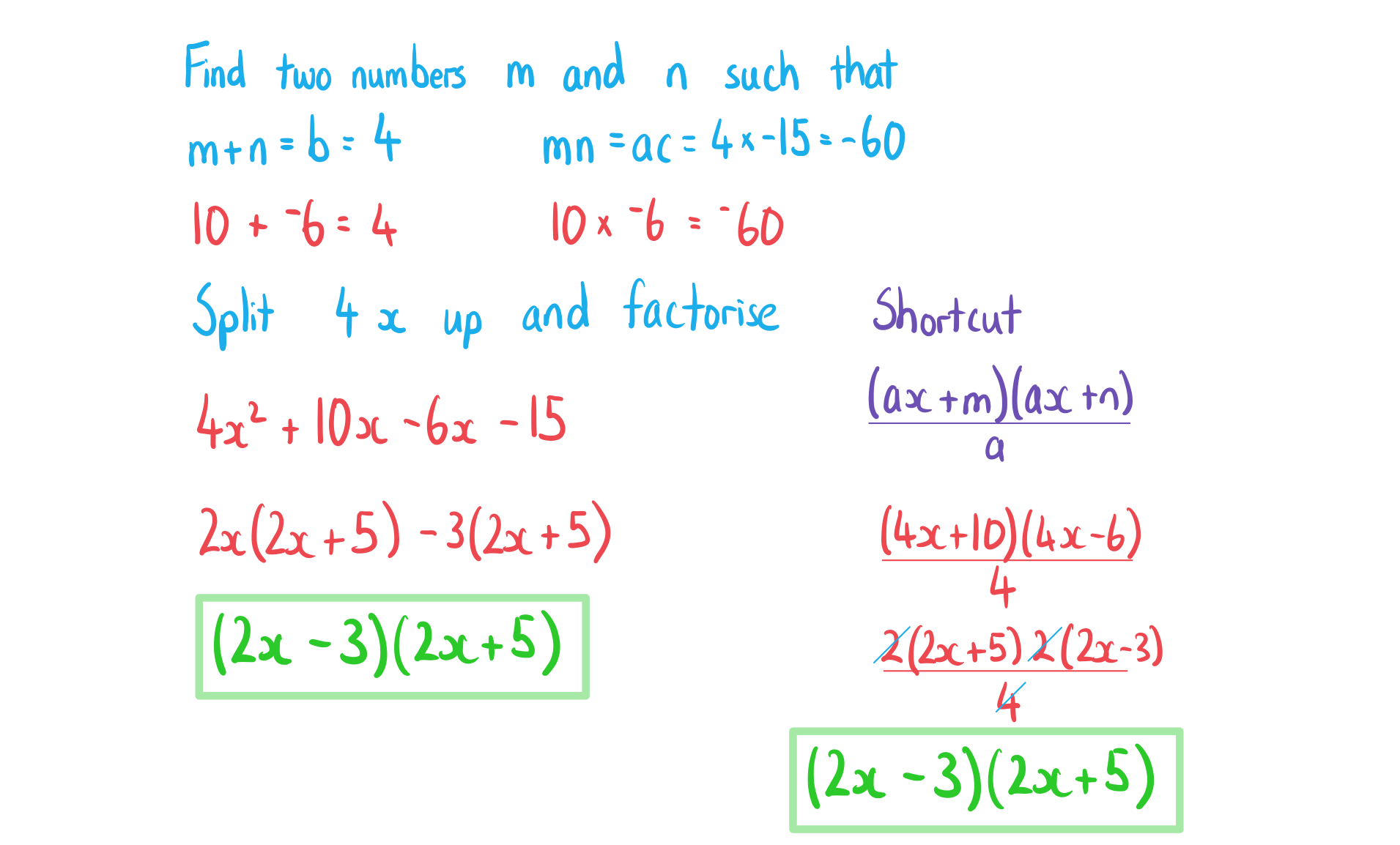
![]()

Completing the Square
Why is completing the square for quadratics useful?
- Completing the square gives the maximum/minimum of a quadratic function
- This can be used to define the range of the function
- It gives the vertexwhen drawing the graph
- It can be used to solve quadratic equations
- It can be used to derive the quadratic formula
How do I complete the square for a monic quadratic of the form x2+ bx + c?
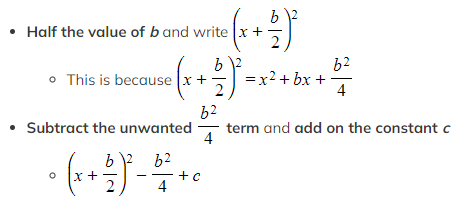 How do I complete the square for a non-monic quadratic of the form ax2+ bx + c?
How do I complete the square for a non-monic quadratic of the form ax2+ bx + c?
 Exam Tip
Exam Tip
 Worked Example
Worked Example
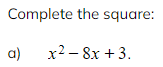
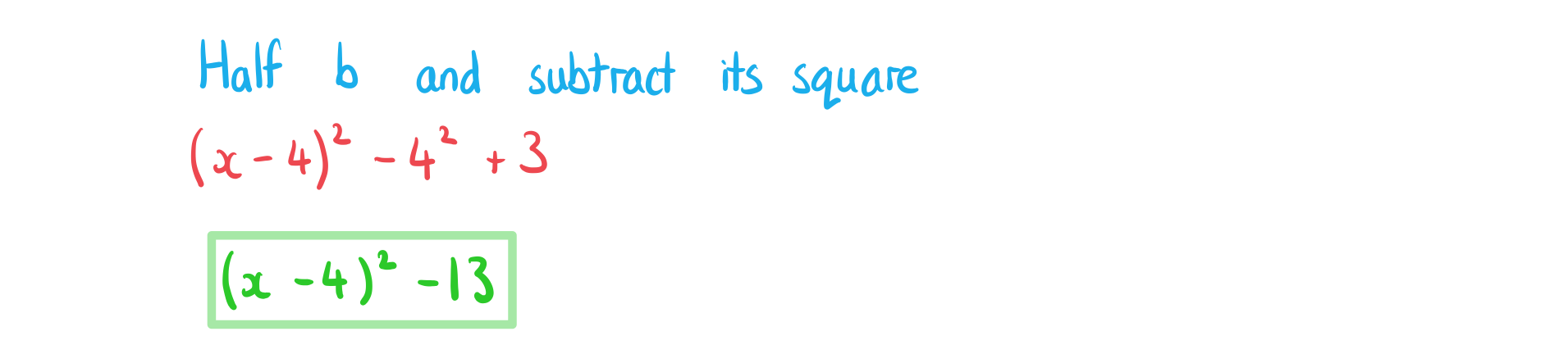
![]()
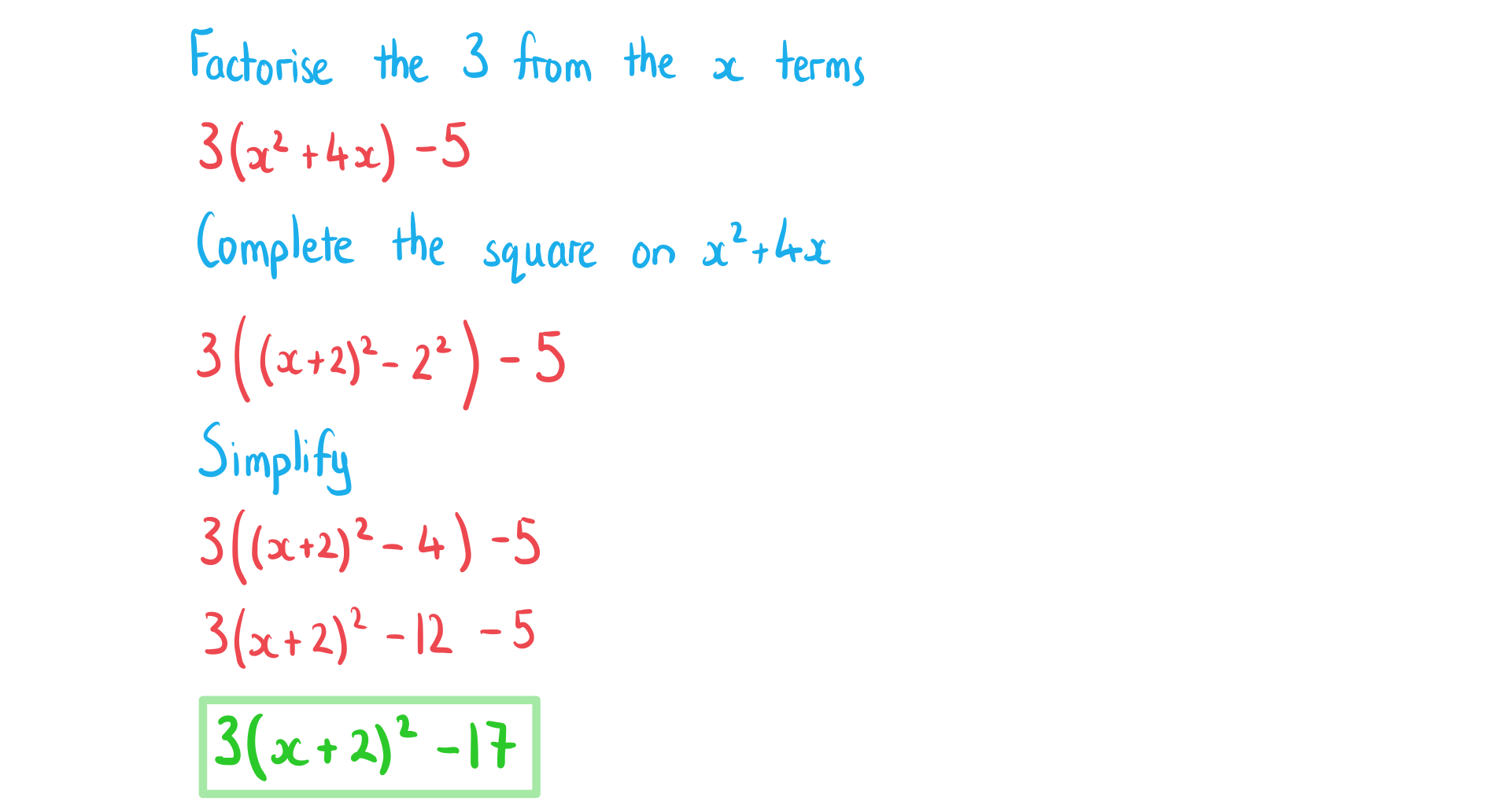
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








