IB DP Maths: AA SL复习笔记1.5.1 Binomial Theorem
Binomial Theorem
What is the Binomial Theorem?
- The binomial theorem (sometimes known as the binomial expansion) gives a method for expanding a two-term expression in a bracket raised to a power
- A binomial expression is in fact any two terms inside the bracket, however in IB the expression will usually be linear
- To expand a bracket with a two-term expression in:
- First choose the most appropriate parts of the expression to assign to a and b
- Then use the formula for the binomial theorem:
How do I find the coefficient of a single term?
- Most of the time you will be asked to find the coefficient of a term, rather than carry out the whole expansion
- Use the formula for the general term
Exam Tip
- Binomial expansion questions can get messy, use separate lines to keep your working clear and always put terms in brackets
Worked Example
The Binomial Coefficient nCr
Make sure you can find and use the button on your G
Exam Tip- You will most likely need to use the formula for nCr at some point in your exam
- Practice using it and don't always rely on your GDC
- Make sure you can find it easily in the formula booklet
Worked Example
Pascal's Triangle
What is Pascal’s Triangle?
- Pascal’s triangle is a way of arranging the binomial coefficients and neatly shows how they are formed
- Each term is formed by adding the two terms above it
- The first row has just the number 1
- Each row begins and ends with a number 1
- From the third row the terms in between the 1s are the sum of the two terms above it
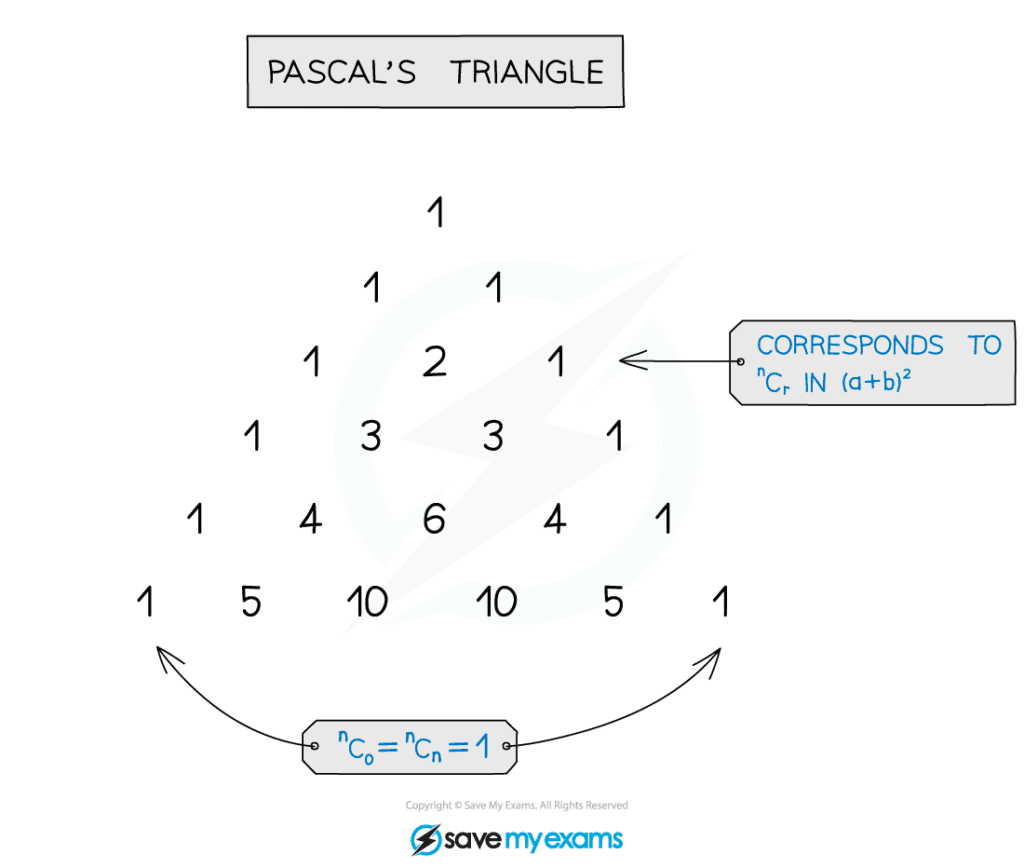
How does Pascal’s Triangle relate to the binomial theorem?
Exam Tip
- In the non-calculator exam Pascal's triangle can be helpful if you need to get the coefficients of an expansion quickly, provided the value of n is not too big
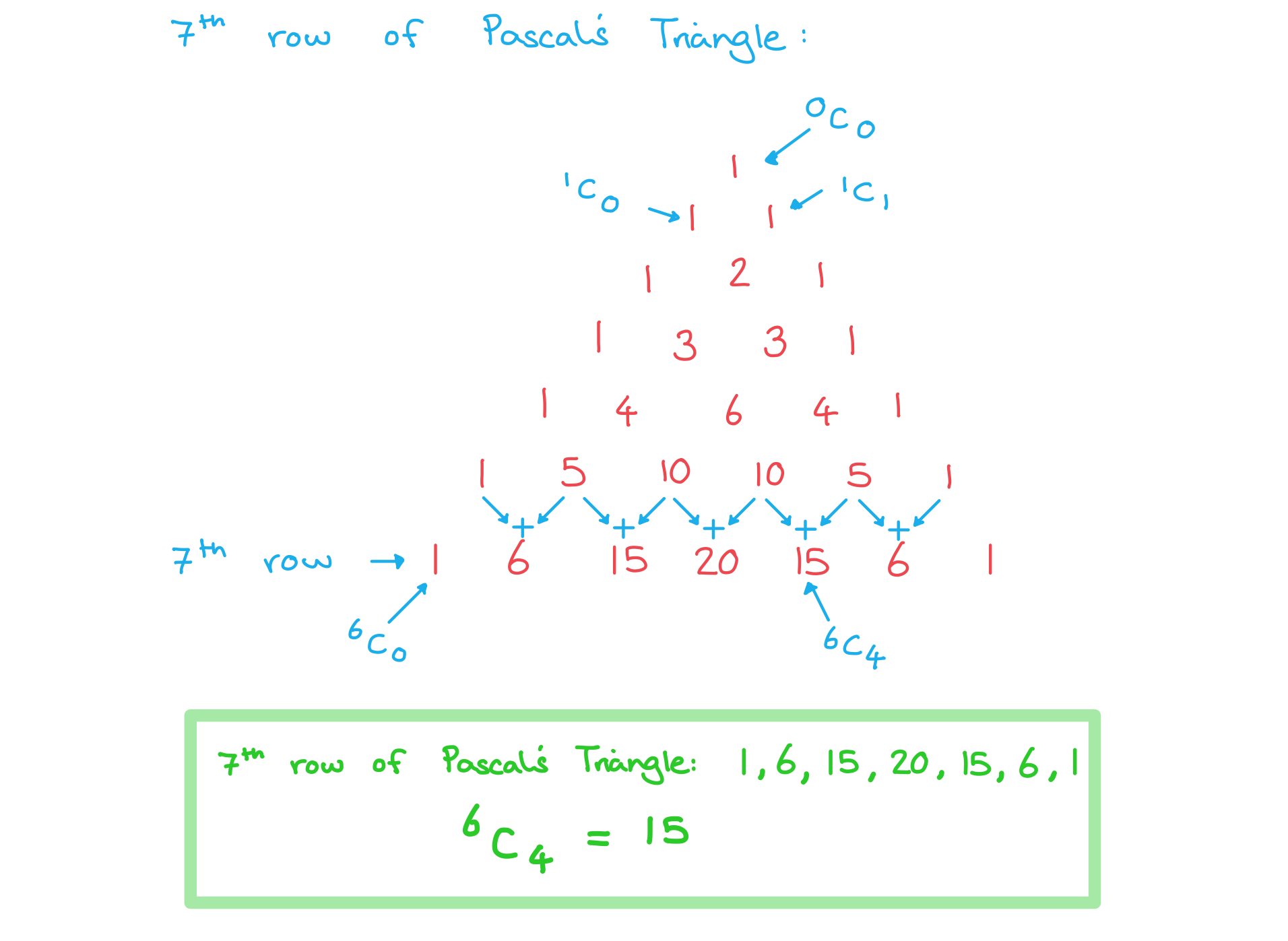
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
欧几里得竞赛 寒假集训班开课了！
AMC8备考管家服务全新上线！
