- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记5.10.3 Modelling with Differential Equations
Modelling with Differential Equations
Why are differential equations used to model real-world situations?
- A differential equation is an equation that contains one or more derivatives
- Derivatives deal with rates of change, and with the way that variables change with respect to one another
- Therefore differential equations are a natural way to model real-world situations involving change
- Most frequently in real-world situations we are interested in how things change over time, so the derivatives used will usually be with respect to time t
How do I set up a differential equation to model a situation?
- An exam question may require you to create a differential equation from information provided
- The question will provide a context from which the differential equation is to be created
- Most often this will involve the rate of change of a variable being proportional to some function of the variable
-
- For example, the rate of change of a population of bacteria, P, at a particular time may be proportional to the size of the population at that time
- For example, the rate of change of a population of bacteria, P, at a particular time may be proportional to the size of the population at that time
-
 Worked Example
Worked Example
a) In a particular pond, the rate of change of the area covered by algae, A, at any time t is directly proportional to the square root of the area covered by algae at that time. Write down a differential equation to model this situation.

b) Newton’s Law of Cooling states that the rate of change of the temperature of an object, T, at any time t is proportional to the difference between the temperature of the object and the ambient temperature of its surroundings, Ta , at that time. Assuming that the object starts off warmer than its surroundings, write down the differential equation implied by Newton’s Law of Cooling.

The Logistic Equation
What is the logistic equation?
 How do I solve problems that involve a logistic equation model?
How do I solve problems that involve a logistic equation model?
- Solving the differential equation will generally involve the technique of separation of variables
- Usually this will also involve rearranging one of the integrals using partial fractions (see the worked example below for an example)
- You will usually be given ‘boundary conditions’ specific to the context of the problem
- For example, you may be told the initial population at time t = 0
- These conditions will allow you to work out the exact value of any integrating constants that occur while solving the differential equation
- You will need to take account of the context of the question in answering the question or in commenting on the model used
Worked Example


b) Find the population of rabbits that the model predicts will be on the island two years after the beginning of the study.
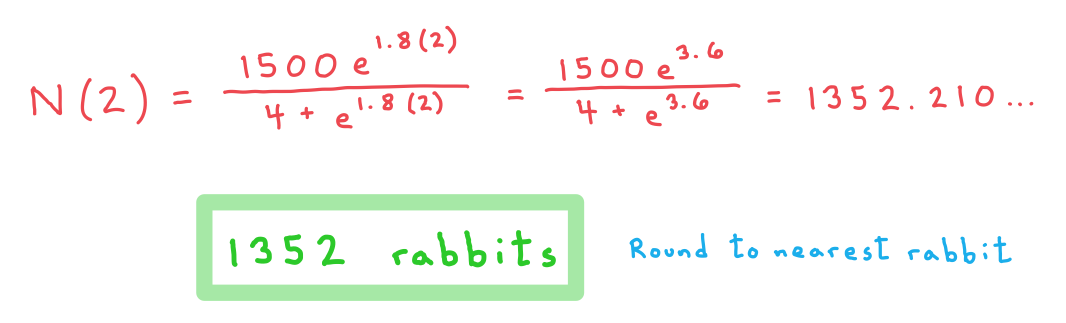
c) Determine the maximum size that the model predicts the population of rabbits can grow to. Justify your answer by an appropriate analysis of the equation in part (a).

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









