IB DP Maths: AA HL复习笔记5.10.1 Numerical Solutions to Differential Equations
First Order Differential Equations
What is a differential equation?
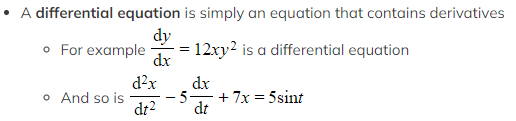What is a first order differential equation?
- A first order differential equation is a differential equation that contains first derivatives but no second (or higher) derivatives
Wait – haven’t I seen first order differential equations before?
- Yes you have!
- In this section of the course you learn how to solve differential equations that can’t just be solved right away by integrating
Euler’s Method: First Order
What is Euler’s method?
- Euler’s method is a numerical method for finding approximate solutions to differential equations
- It treats the derivatives in the equation as being constant over short ‘steps’
- The accuracy of the Euler’s Method approximation can be improved by making the step sizes smaller
How do I use Euler’s method with a first order differential equation?
Exam Tip
- Be careful with letters – in the equations in the exam, and in your GDC’s recursion calculator, the variables may not be x and y
- If an exam question asks you how to improve an Euler’s method approximation, the answer will almost always have to do with decreasing the step size!
Worked Example
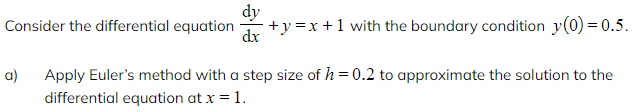
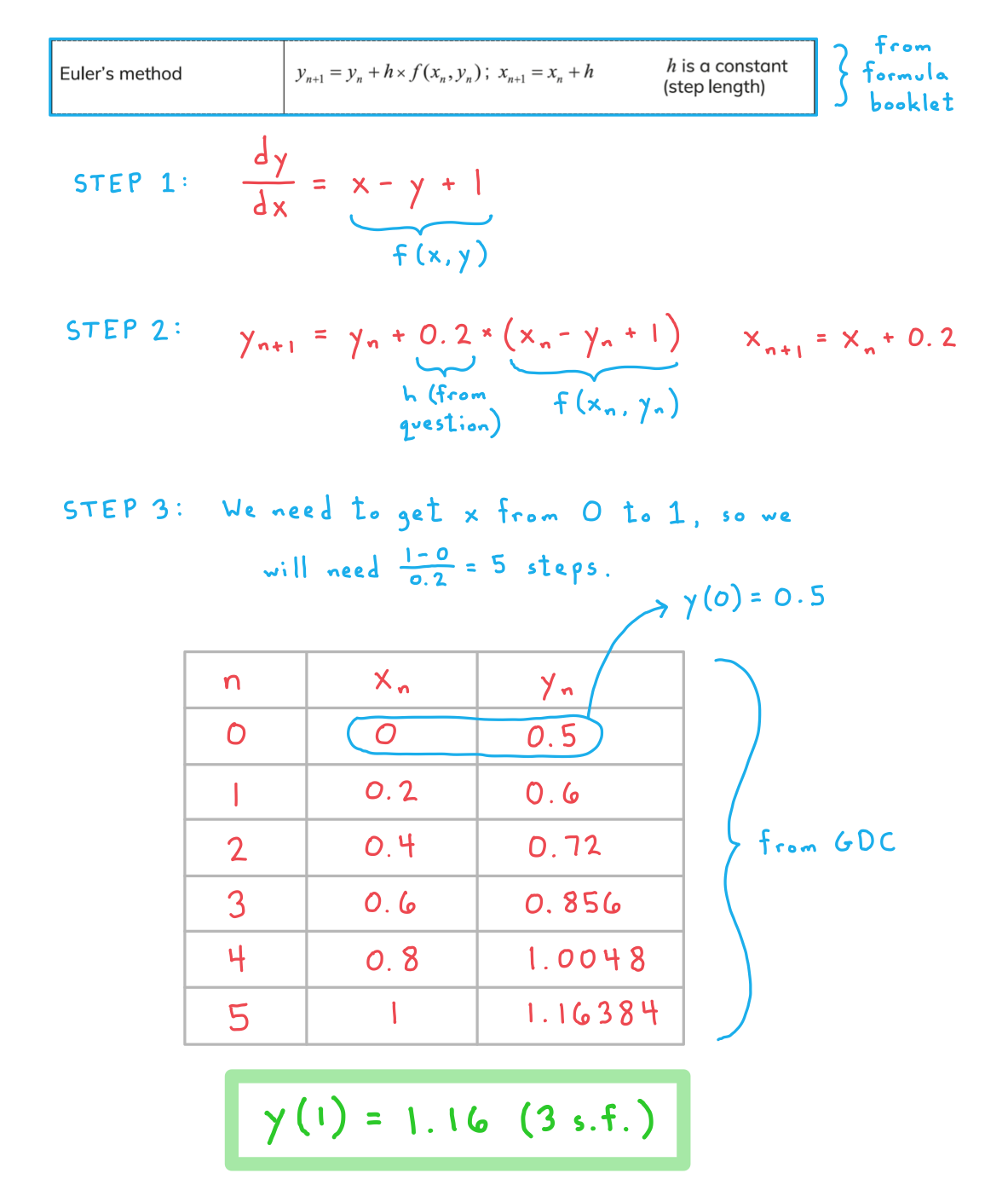
b) Explain how the accuracy of the approximation in part (a) could be improved.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
