- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记8.2.3 Half-Life
Half-Life
- Half-life is defined as:
The time taken for the initial number of nuclei to halve for a particular isotope
- This means when a time equal to the half-life has passed, the activity of the sample will also half
- This is because the activity is proportional to the number of undecayed nuclei, A ∝ N
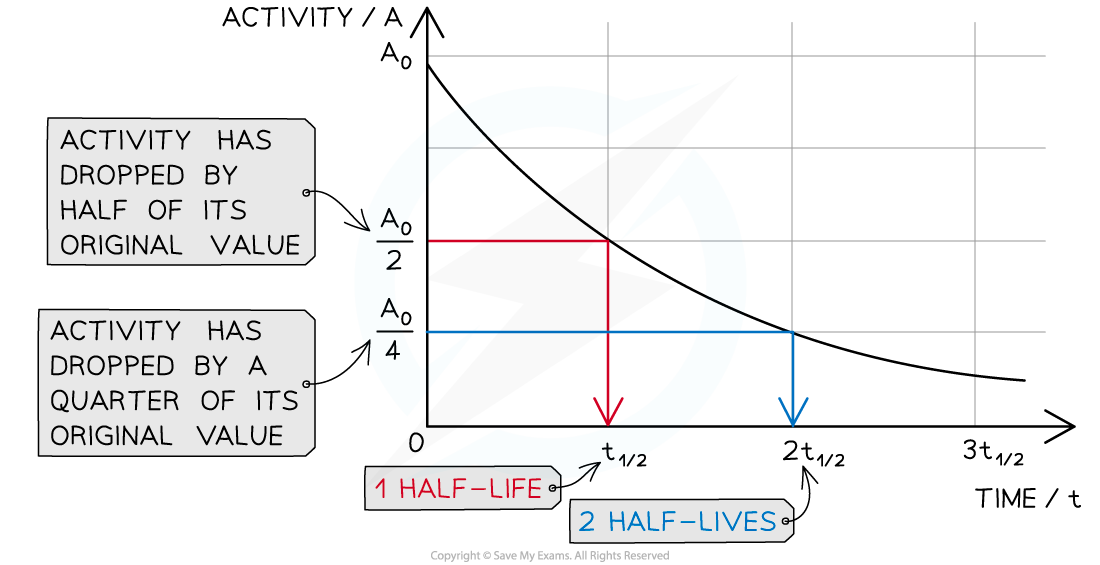
When a time equal to the half-life passes, the activity falls by half, when two half-lives pass, the activity falls by another half (which is a quarter of the initial value)
- To find an expression for half-life, start with the equation for exponential decay:
N = N0 e–λt
- Where:
- N = number of nuclei remaining in a sample
- N0 = the initial number of undecayed nuclei (when t = 0)
- λ = decay constant (s-1)
- t = time interval (s)
- When time t is equal to the half-life t½, the activity N of the sample will be half of its original value, so N = ½ N0
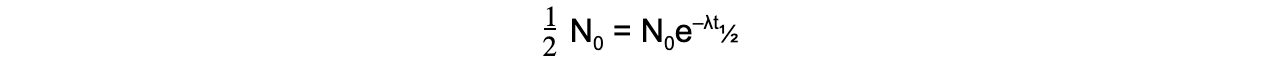
- The formula can then be derived as follows:
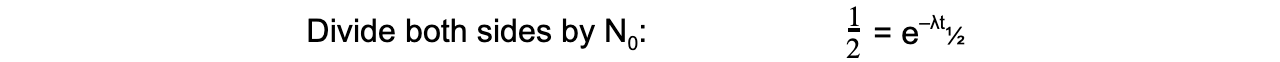


- Therefore, half-life t½ can be calculated using the equation:
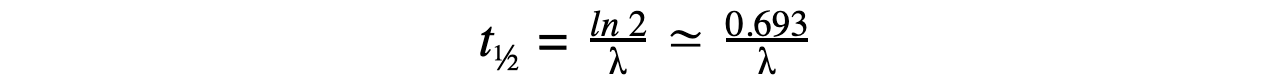
- This equation shows that half-life t½ and the radioactive decay rate constant λ are inversely proportional
- Therefore, the shorter the half-life, the larger the decay constant and the faster the decay
Worked Example
Strontium-90 is a radioactive isotope with a half-life of 28.0 years.A sample of Strontium-90 has an activity of 6.4 × 109 Bq.Calculate the decay constant λ, in s–1, of Strontium-90.
Step 1: Convert the half-life into seconds
-
- t½ = 28 years = 28 × 365 × 24 × 60 × 60 = 8.83 × 108 s
Step 2: Write the equation for half-life
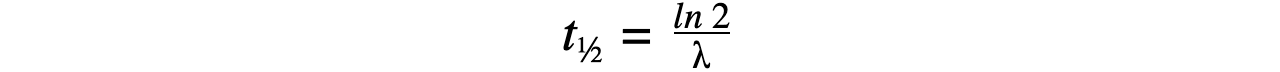
Step 3: Rearrange for λ and calculate
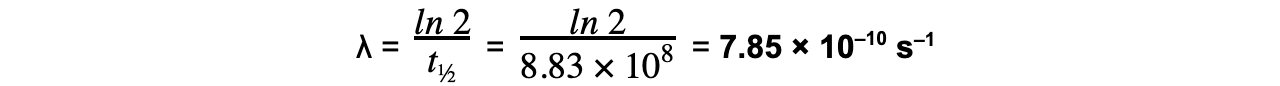
Exam Tip
Although you may not be expected to derive the half-life equation, make sure you're comfortable with how to use it in calculations such as that in the worked example.
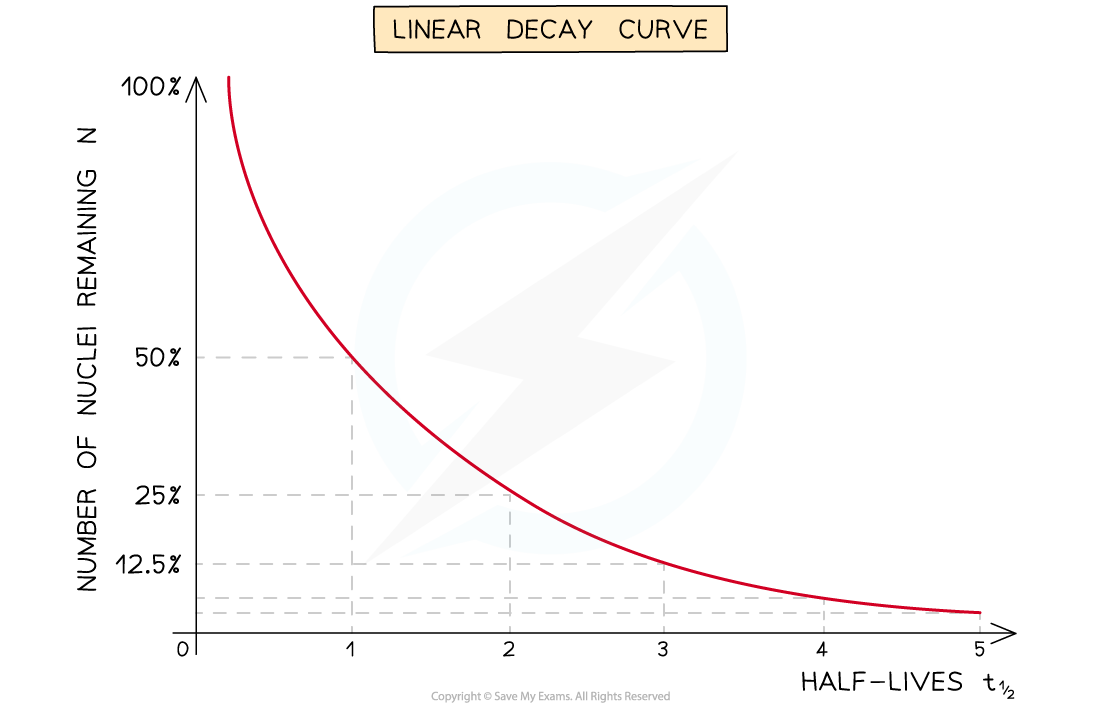
Half-Life from Decay Curves
- The half-life of a radioactive substance can be determined from decay curves and log graphs
- Since half-life is the time taken for the initial number of nuclei, or activity, to reduce by half, it can be found by
- Drawing a line to the curve at the point where the activity has dropped to half of its original value
- Drawing a line from the curve to the time axis, this is the half-life
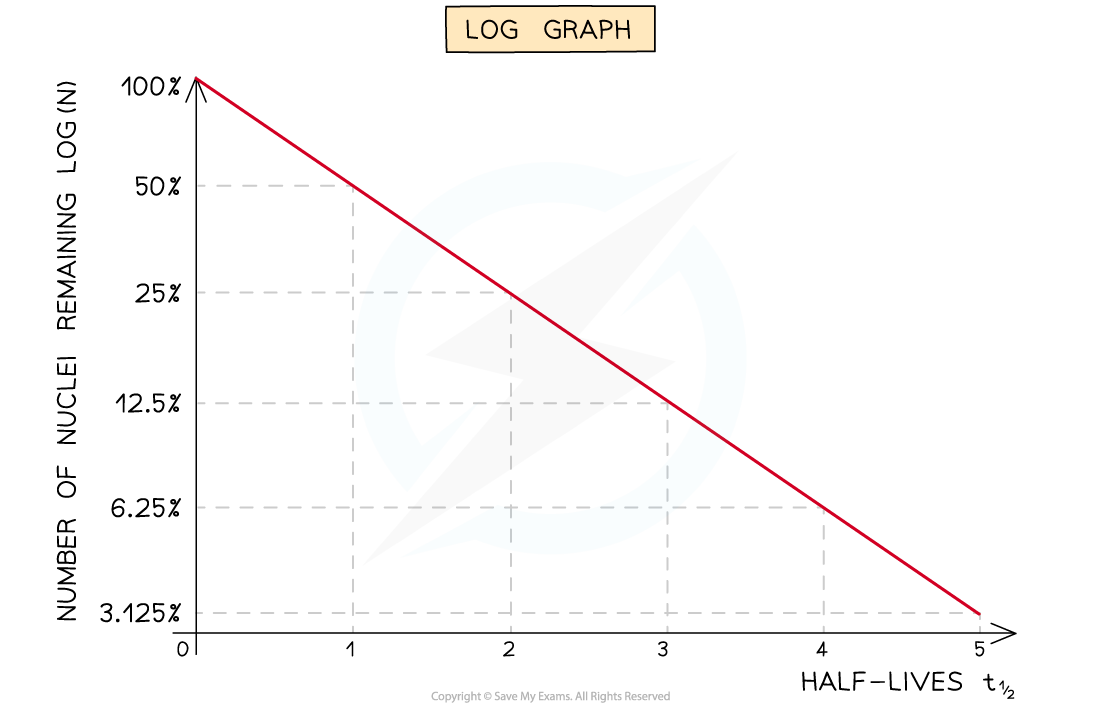
Log Graphs
- Straight-line graphs tend to be more useful than curves for interpreting data
- Nuclei decay exponentially, therefore, to achieve a straight line plot, logarithms can be used
- Take the exponential decay equation for the number of nuclei
N = N0 e–λt
- Taking the natural logs of both sides
ln N = ln (N0) − λt
- In this form, this equation can be compared to the equation of a straight line
y = mx + c
- Where:
- ln (N) is plotted on the y-axis
- t is plotted on the x-axis
- gradient = −λ
- y-intercept = ln (N0)
- Half-lives can be found in a similar way to the decay curve but the intervals will be regular as shown below:
Worked Example
The radioisotope technetium is used extensively in medicine. The graph below shows how the activity of a sample varies with time. Determine:
Determine:
a) The decay constant for technetium
b) The number of technetium atoms remaining in the sample after 24 hours
Part (a)
Step 1: Draw lines on the graph to determine the time it takes for technetium to drop to half of its original activity

Step 2: Read the half-life from the graph and convert to seconds
-
- t ½ = 6 hours = 6 × 60 × 60 = 21 600 s
Step 3: Write out the half life equation
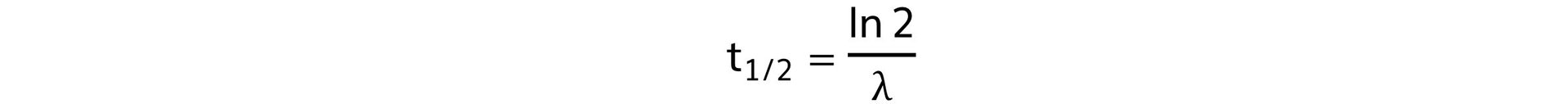 Step 4: Calculate the decay constant
Step 4: Calculate the decay constant
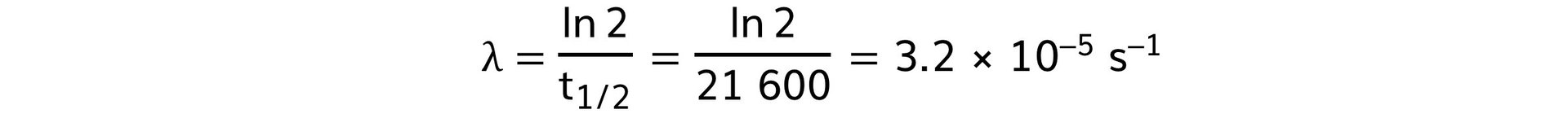
Part (b)
Step 1: Draw lines on the graph to determine the activity after 24 hours

-
- At t = 24 hours, A = 0.5 × 107 Bq
Step 2: Write out the activity equation
A = λN
Step 3: Calculate the number of atoms remaining in the sample
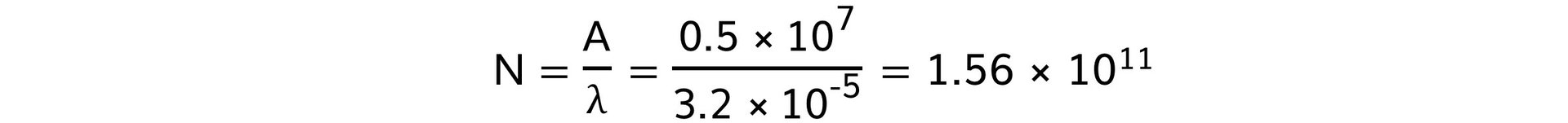
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









