AQA A Level Physics复习笔记7.9.5 Applications of EM Induction

• Similar to a coil or a solenoid, a straight conducting rod moving through a magnetic field will also have an e.m.f induced in it
• This is only when the conductor moves perpendicular to the magnetic field lines where it cuts through the magnetic flux lines

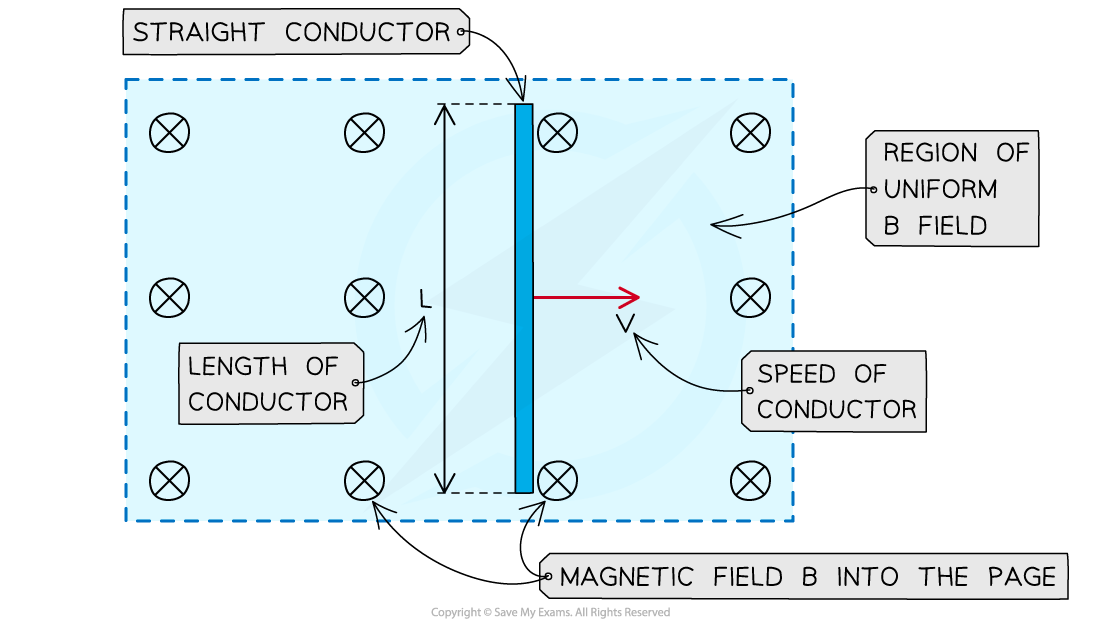
Conducting rod moving perpendicular to a magnetic field directed into the page

• The conducting rod has a length L and moves through a uniform magnetic field with flux density B at a constant velocity v
• The distance travelled by the conductor is:

s = vΔt

• Where:
  • s = distance travelled (m)
  • v = velocity (m s-1)
  • Δt = time interval (s)

   

• Therefore, the area A of the magnetic flux that it cuts through is:

A = LvΔt

• The total flux the conductor cuts through is:

ΔΦ = BA = BLvΔt

• Faraday's law gives the e.m.f induced:

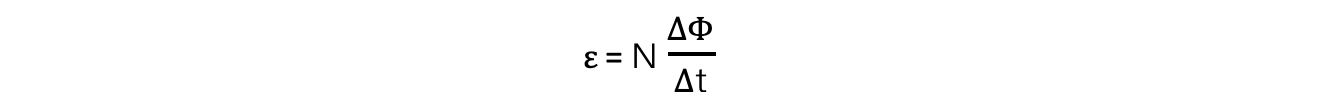
• Where for the conductor, N = 1
• Substituting the change in magnetic flux ΔΦ into the e.m.f equation:

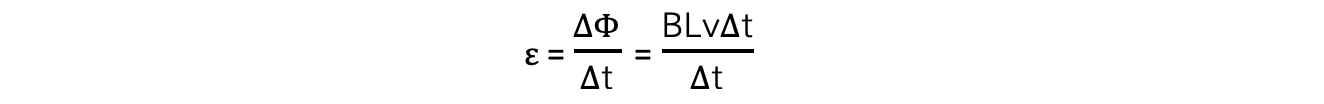
• Therefore, the induced e.m.f in the conductor as it moves through the magnetic field is:

ε = BLv

• This equation shows that the e.m.f induced increases if:
  • A longer conductor is in the field
  • The magnetic field strength is larger
  • The conductor cuts through the field lines faster

   

Step 1: Write down the known quantities

• • Length, L = 34.5 m
  • Velocity, v = 253 m s-1
  • Magnetic field strength, B = 0.06 mT = 0.06 × 10-3 T

   

Step 2: Write down the e.m.f equation

ε = BLv

Step 3: Substitute in the values

ε = (0.06 × 10-3) × 34.5 × 253 = 0.52371 = 0.52 V

• When a coil rotates in a uniform magnetic field, the flux through the coil will vary as it rotates
• Since e.m.f is the rate of change of flux linkage, this means the e.m.f will also change as it rotates
  • The maximum e.m.f is when the coil cuts through the most field lines
  • The e.m.f induced is an alternating voltage

   

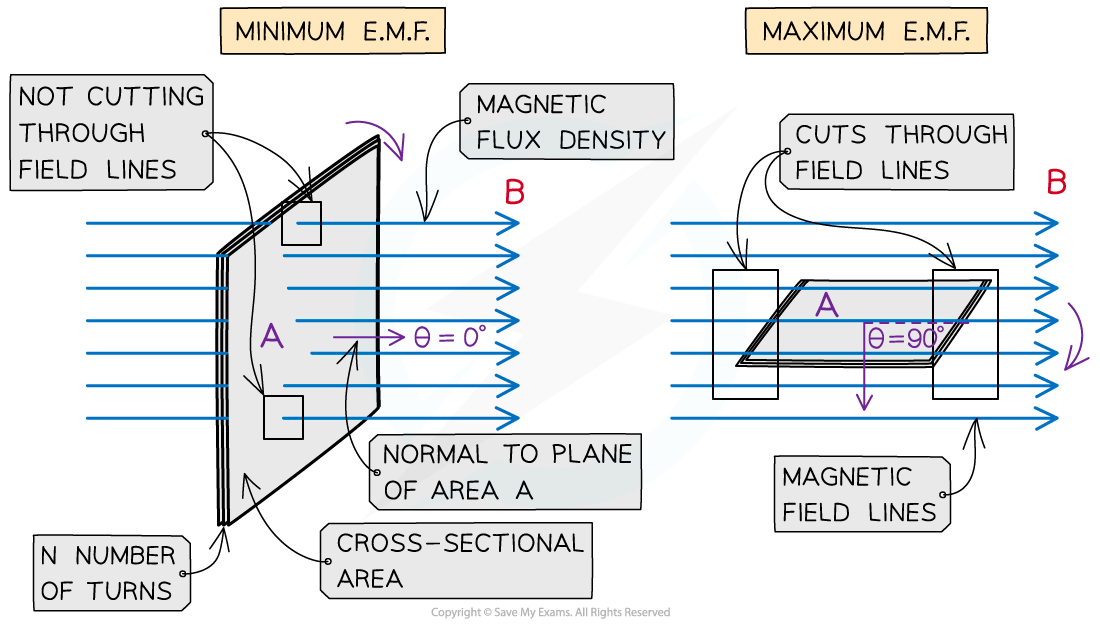
The maximum e.m.f is when the coil cuts through the field lines when they are parallel to the plane of the coil

• This means that the e.m.f is:
  • Maximum when θ = 90o. The magnetic field lines are parallel to the plane of the area (or the normal to the area is perpendicular to the field lines)
  • 0 when θ = 0o. The magnetic fields lines are perpendicular to the plane of the area (or the normal to the area is parallel to the field lines)

   

• Note that this is the opposite of the maximum and minimum flux through the coil

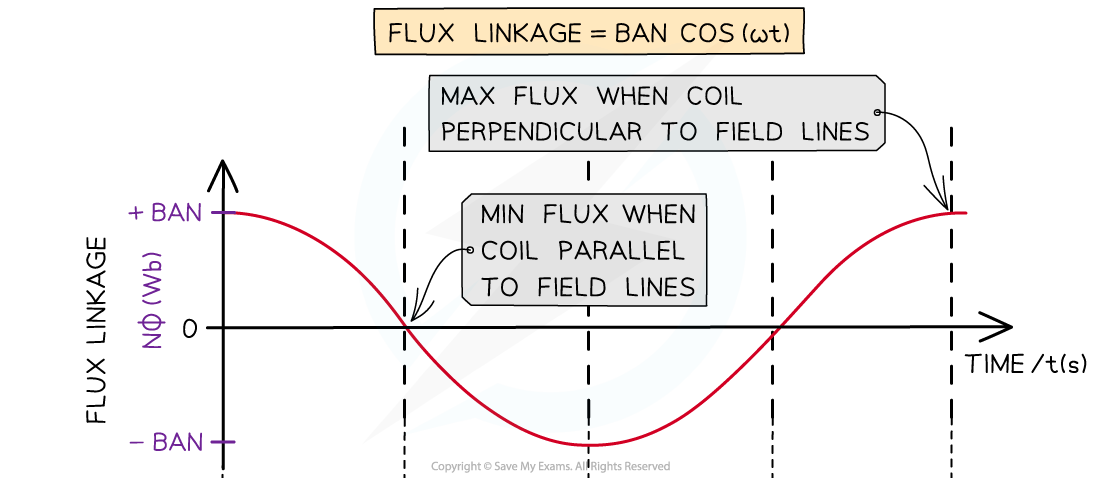
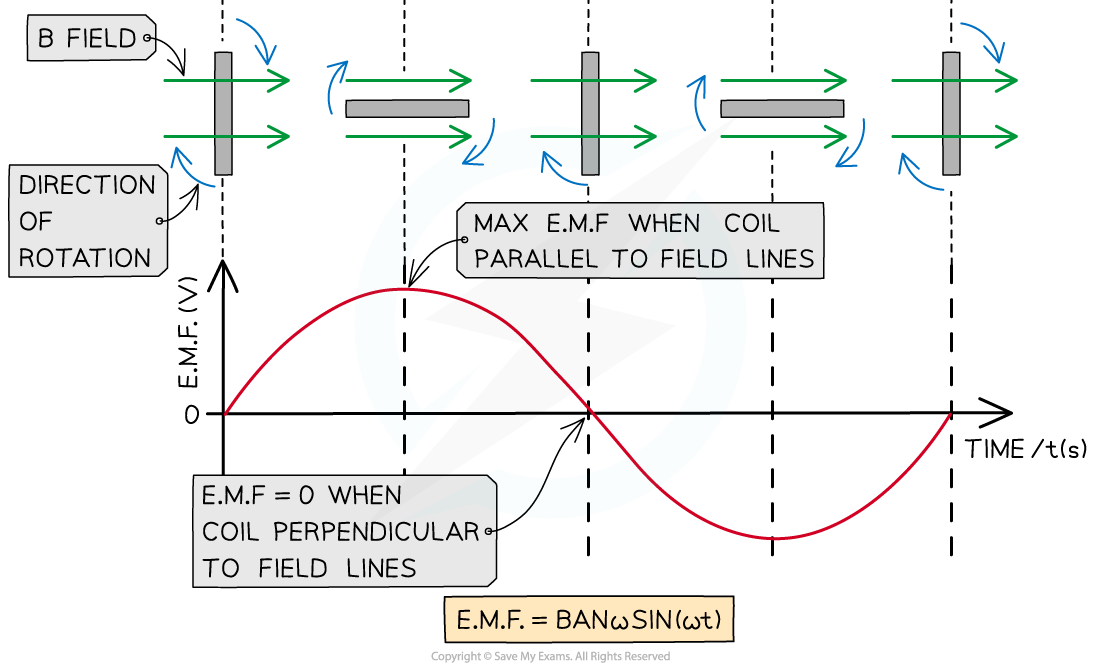
The e.m.f and flux linkage are 90° out of phase

• The flux linkage can also be written as:

NΦ = BAN cos(ωt)

• Where the angle θ depends on the angular speed of the coil, ω:

θ = ωt

• The induced e.m.f, ε from Faraday's Law depends on the rate of change of flux linkage, which means it can also be written as:

ε = BANω sin(ωt)

• Where:
  • ε = e.m.f induced in the coil (V)
  • B = magnetic flux density (T)
  • A = cross-sectional area of the coil (m2)
  • ω = angular speed of the coil (rad s-1)
  • t = time (s)

   

• The equation shows that the e.m.f varies sinusoidally and it is 90° out of phase with the flux linkage

Step 1: Write the known quantities

• • Number of turns, N = 40
  • Area, A = 0.5 m2
  • Angular velocity, ω = 42 rad s-1
  • Magnetic flux density, B = 3.15 mT = 3.15 × 10-3 T

   

Step 2: Write down the e.m.f equation

ε = BANω sin(ωt)

Step 3: Determine when the maximum e.m.f will be

• • The maximum e.m.f occurs when sin(ωt) = ±1, or when the coil is parallel to the magnetic field

Step 4: Substitute in the values

ε = (3.15 × 10-3) × 0.5 × 40 × 42 × ±1 = ± 2.6 V