- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记7.6.3 Energy Stored by a Capacitor
Energy Stored by a Capacitor
- When charging a capacitor, the power supply pushes electrons from the positive to the negative plate
- It therefore does work on the electrons and electrical energy becomes stored on the plates
- At first, a small amount of charge is pushed from the positive to the negative plate, then gradually, this builds up
- Adding more electrons to the negative plate at first is relatively easy since there is little repulsion
- As the charge of the negative plate increases ie. becomes more negatively charged, the force of repulsion between the electrons on the plate and the new electrons being pushed onto it increases
- This means a greater amount of work must be done to increase the charge on the negative plate or in other words:
The potential difference across the capacitor increases as the amount of charge increases
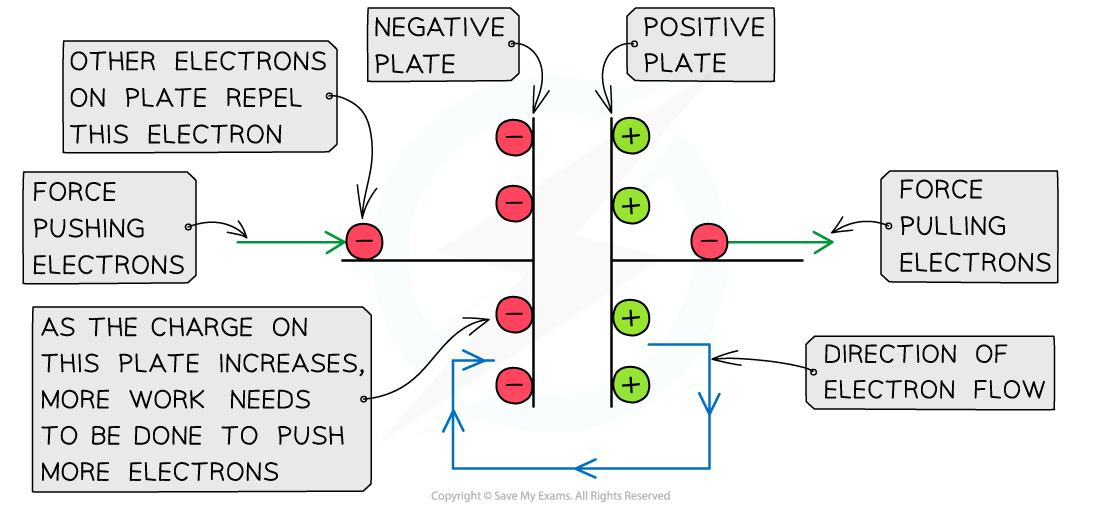
As the charge on the negative plate builds up, more work needs to be done to add more charge
- The charge Q on the capacitor is directly proportional to its potential difference V
- The graph of charge against potential difference is therefore a straight line graph through the origin
- The electrical (potential) energy stored in the capacitor can be determined from the area under the potential-charge graph which is equal to the area of a right-angled triangle:
Area = 0.5 × base × height
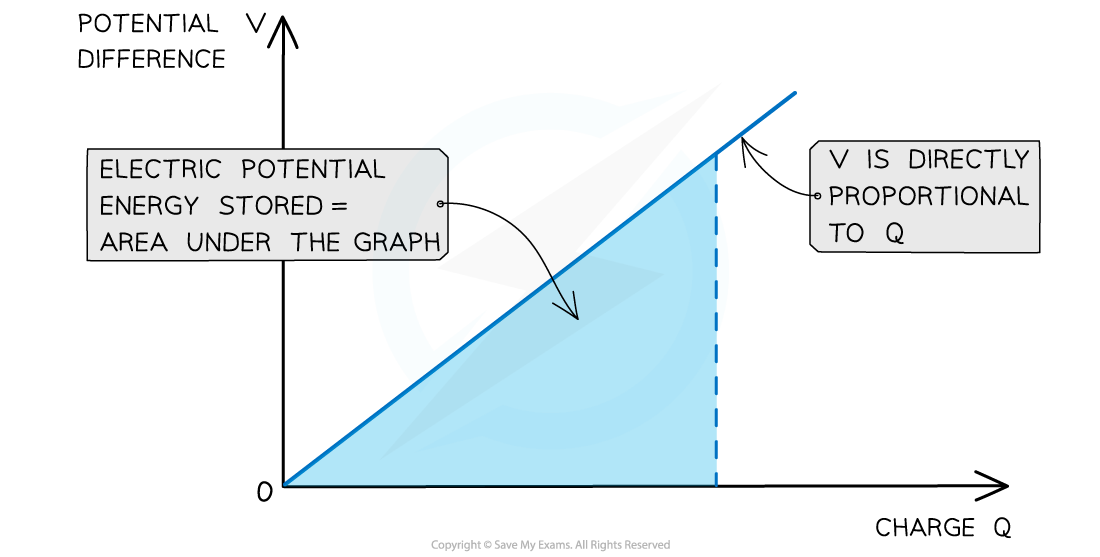
The electric energy stored in the capacitor is the area under the potential-charge graph
- Therefore the work done, or energy stored in a capacitor is defined by the equation:
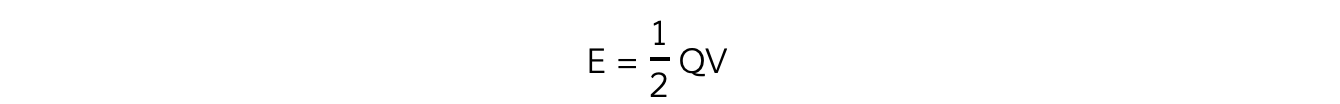
- Where:
- E = work done or energy stored (J)
- Q = charge (C)
- V = potential difference (V)
- Substituting the charge with the capacitance equation Q = CV, the energy stored can also be defined as:
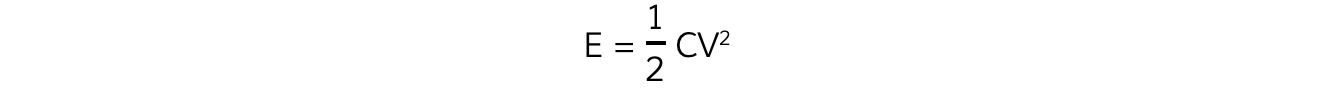
- By substituting the potential V, the energy stored can also be defined in terms of just the charge, Q and the capacitance, C:
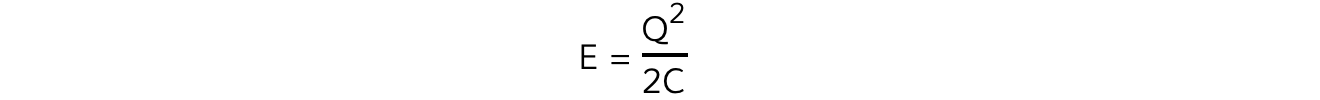
Worked Example
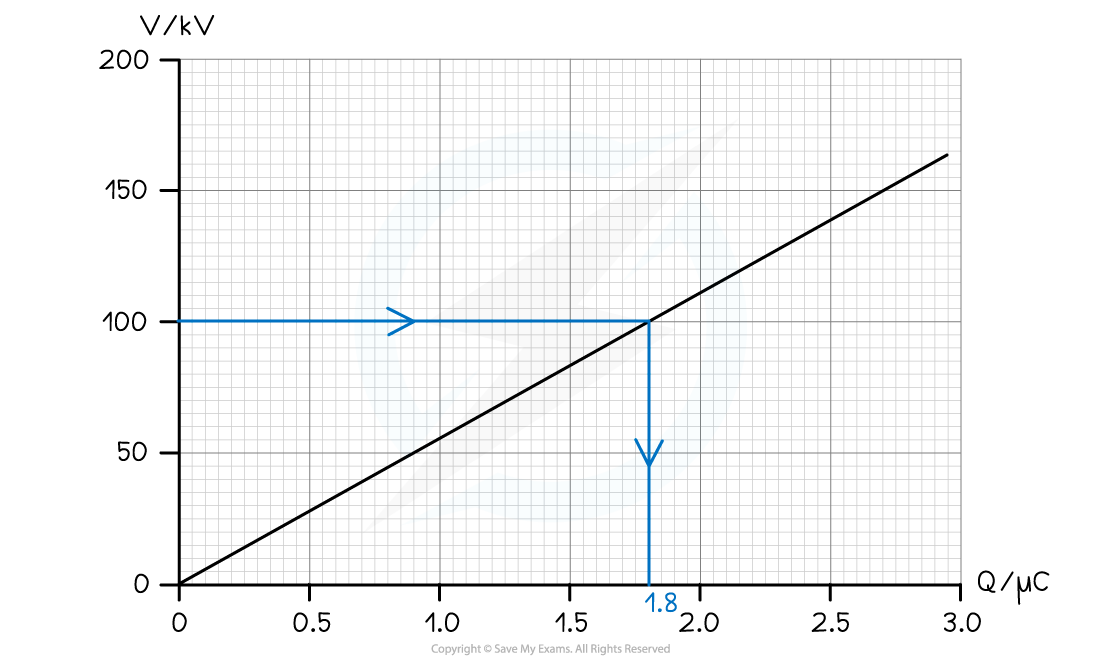
The variation of the potential V of a charged isolated metal sphere with surface charge Q is shown on the graph below. Using the graph, determine the electric potential energy stored on the sphere when charged to a potential of 100 kV.
Using the graph, determine the electric potential energy stored on the sphere when charged to a potential of 100 kV.
Step 1: Determine the charge on the sphere at the potential of 100 kV
-
- From the graph, the charge on the sphere at 100 kV is 1.8 μC
Step 2: Calculate the electric potential energy stored
-
- The energy stored is equal to the area under the graph at 100 kV
- The area is equal to a right-angled triangle, so, can be calculated with the equation:
Area = 0.5 × base × height
Area = 0.5 × 1.8 μC × 100 kV
Energy E = 0.5 × (1.8 × 10-6) × (100 × 103) = 0.09 J
Worked Example
Calculate the change in the energy stored in a capacitor of capacitance 1500 μF when the potential difference across the capacitor changes from 10 V to 30 V.
Step 1: Write down the equation for energy stored, in terms of C and V and list the known values
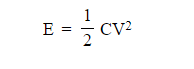
Capacitance, C = 1500μF
Final p.d, V2 = 30 V
Initial p.d V1 =10 V
Step 2: The change in energy stored in proportional to the change in p.d

Step 3: Substitute in the values
Exam Tip
All 3 equations for the energy stored will be given on your data sheet. To figure out which to use, check what variables (C, Q or V) have already been given in the question.
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








