- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记3.10.3 Pairs of Lines in 3D
Coincident, Parallel, Intersecting & Skew Lines
How do I tell if two lines are parallel?
- Two lines are parallel if, and only if, their direction vectors are parallel
- This means the direction vectors will be scalar multiples of each other
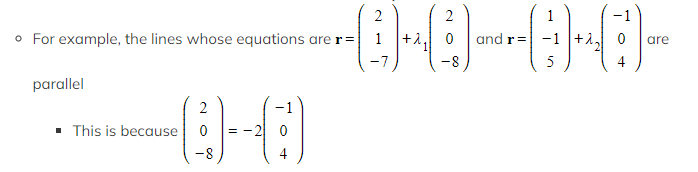 How do I tell if two lines are coincident?
How do I tell if two lines are coincident?
- Coincident lines are two lines that lie directly on top of each other
- They are indistinguishable from each other
- Two parallel lines will either never intersect or they are coincident (identical)
- Sometimes the vector equations of the lines may look different
-
- If two parallel lines share any point, then they share all points and are coincident
- Sometimes the vector equations of the lines may look different
What are skew lines?
- Lines that are not parallel and which do not intersect are called skew lines
- This is only possible in 3-dimensions
How do I determine whether lines in 3 dimensions are parallel, skew, or intersecting?
- First, look to see if the direction vectors are parallel:
- if the direction vectors are parallel, then the lines are parallel
- if the direction vectors are not parallel, the lines are not parallel
- If the lines are parallel, check to see if the lines are coincident:
- If they share any point, then they are coincident
- If any point on one line is not on the other line, then the lines are not coincident
- If the lines are not parallel, check whether they intersect:
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
- e.g. λ and μ, for the parameters
- STEP 2: Write the three separate equations for the i, j, and k components in terms ofλ and μ
- STEP 3: Solve two of the equations to find a value for λ and μ
- STEP 4: Check whether the values of λ and μ you have found satisfy the third equation
- If all three equations are satisfied, then the lines intersect
- If not all three equations are satisfied, then the lines are skew
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
How do I find the point of intersection of two lines?
- If a pair of lines are not parallel and do intersect, a unique point of intersection can be found
- If the two lines intersect, there will be a single point that will lie on both lines
- Follow the steps above to find the values of λ and μ that satisfy all three equations
- STEP 5: Substitute either the value of λ or the value of μ into one of the vector equations to find the position vector of the point where the lines intersect
- It is always a good idea to check in the other equations as well, you should get the same point for each line
Exam Tip
 Worked Example
Worked Example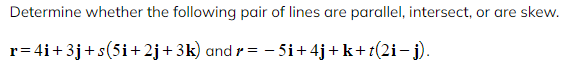

Angle Between Two Lines
How do we find the angle between two lines?
- The angle between two lines is equal to the angle between their direction vectors
- It can be found using the scalar product of their direction vectors
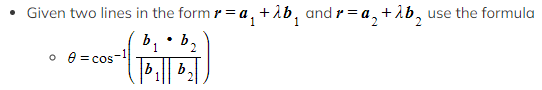 If you are given the equations of the lines in a different form or two points on a line you will need to find their direction vectors first
If you are given the equations of the lines in a different form or two points on a line you will need to find their direction vectors first- To find the angle ABC the vectors BA and BC would be used, both starting from the point B
- The intersection of two lines will always create two angles, an acute one and an obtuse one
- These two angles will add to 180°
- You may need to subtract your answer from 180° to find the angle you are looking for
- A positive scalar product will result in the acute angle and a negative scalar product will result in the obtuse angle
- Using the absolute value of the scalar product will always result in the acute angle
Exam Tip
- In your exam read the question carefully to see if you need to find the acute or obtuse angle
- When revising, get into the practice of double checking at the end of a question whether your angle is acute or obtuse and whether this fits the question
Worked Example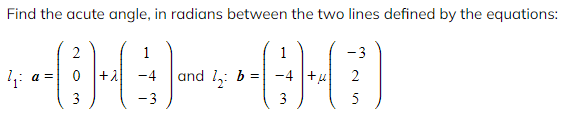

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1










