- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记3.9.1 Introduction to Vectors
Scalars & Vectors
What are scalars?
- Scalars are quantities without direction
- They have only a size (magnitude)
- For example: speed, distance, time, mass
- Most scalar quantities can never be negative
- You cannot have a negative speed or distance
What are vectors?
- Vectors are quantities which also have a direction, this is what makes them more than just a scalar
- For example: two objects with velocities of 7 m/s and ‑7 m/s are travelling at the same speed but in opposite directions
- A vector quantity is described by both its magnitude and direction
- A vector has components in the direction of the x- , y-, and z- axes
- Vector quantities can have positive or negative components
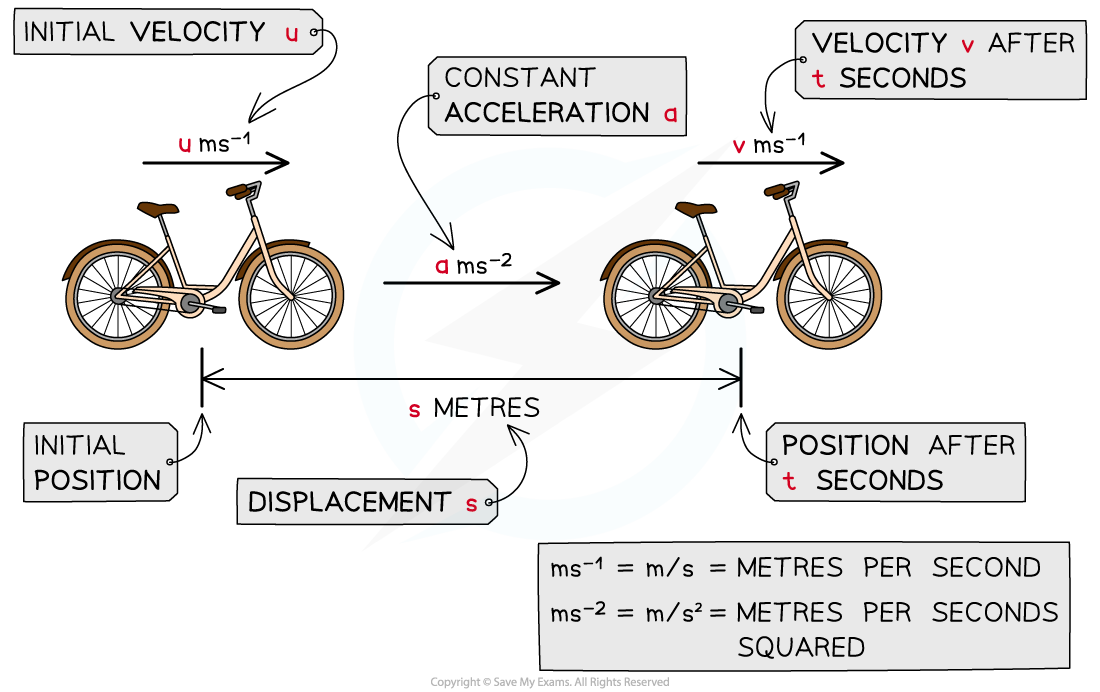
- Some examples of vector quantities you may come across are displacement, velocity, acceleration, force/weight, momentum
- Displacement is the position of an object from a starting point
- Velocity is a speed in a given direction (displacement over time)
- Acceleration is the change in velocity over time
- Vectors may be given in either 2- or 3- dimensions
Exam Tip
- Make sure you fully understand the definitions of all the words in this section so that you can be clear about what your exam question is asking of you
Worked Example
State whether each of the following is a scalar or a vector quantity.
a) A speed boat travels at 3 m/s on a bearing of 052°

b) A garden is 1.7 m wide

c) A car accelerates forwards at 5.4 ms-2

d) A film lasts 2 hours 17 minutes

e) An athlete runs at an average speed of 10.44 ms-1

f) A ball rolls forwards 60 cm before stopping

Vector Notation
How are vectors represented?
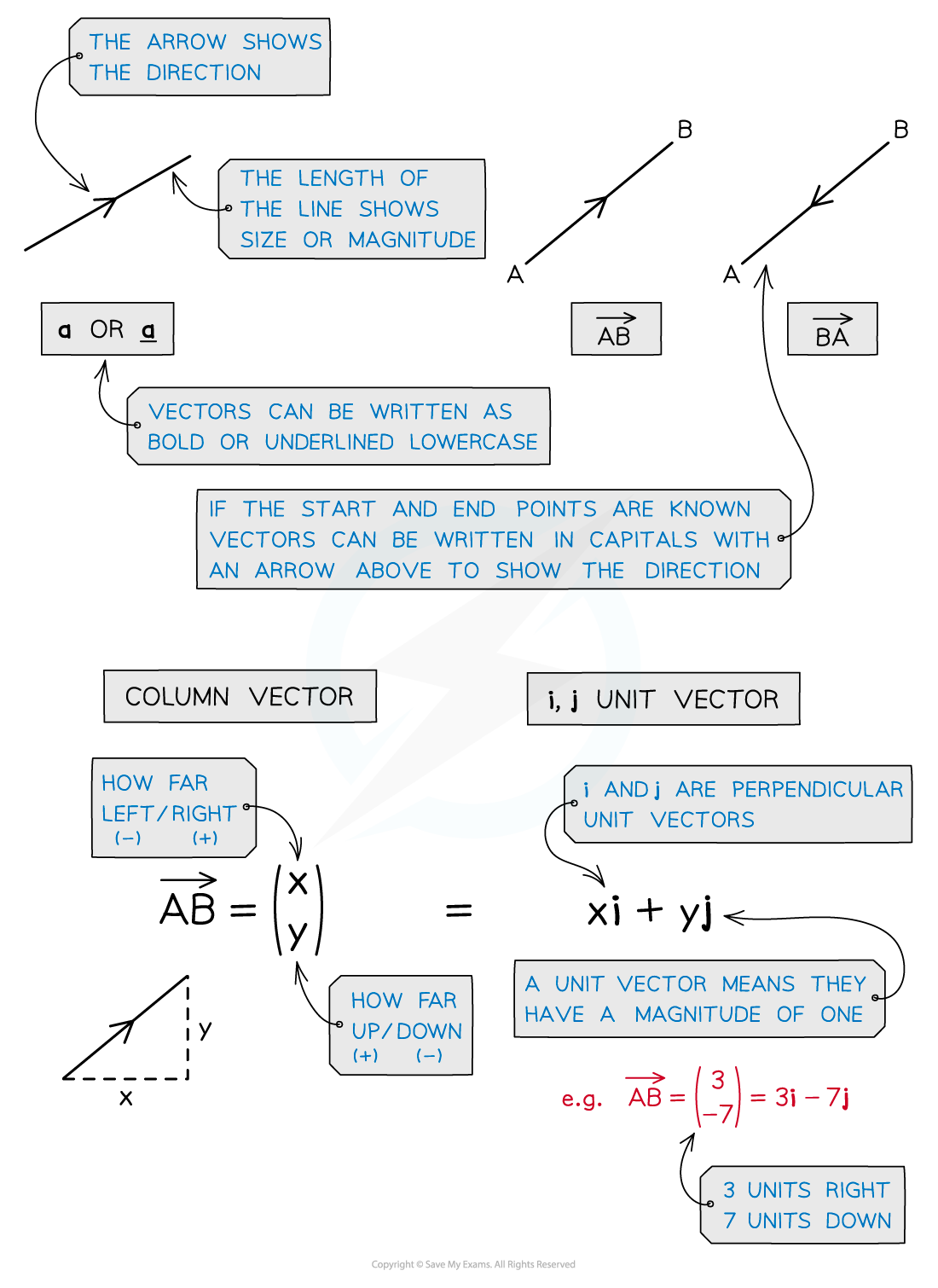
- Vectors are usually represented using an arrow in the direction of movement
- The length of the arrow represents its magnitude
- They are written as lowercase letters either in bold or underlined
- For example a vector from the point O to A will be written a or a
- The vector from the point A to O will be written -a or -a
- For example a vector from the point O to A will be written a or a
- If the start and end point of the vector is known, it is written using these points as capital letters with an arrow showing the direction of movement
 Two vectors are equal only if their corresponding components are equal
Two vectors are equal only if their corresponding components are equal- Numerically, vectors are either represented using column vectors or base vectors
- Unless otherwise indicated, you may carry out all working and write your answers in either of these two types of vector notation
What are column vectors?
- Column vectors are where one number is written above the other enclosed in brackets
- In 2-dimensions the top number represents movement in the horizontal direction (right/left) and the bottom number represents movement in the vertical direction (up/down)
- A positive value represents movement in the positive direction (right/up) and a negative value represents movement in the negative direction (left/down)
 What are base vectors?
What are base vectors?
- Base vectors use i, j and k notation where i, j and k are unit vectors in the positive x, y, and z directions respectively
- This is sometimes also called unit vector notation
- A unit vector has a magnitude of 1
- In 2-dimensions i represents movement in the horizontal direction (right/left) and j represents the movement in the vertical direction (up/down)
- For example: The vector (-4i + 3j) would mean 4 units in the negative horizontal (x) direction (i.e., left) and 3 units in the positive vertical (y) direction (i.e., up)
- In 3-dimensions i represents movement in the x direction (length), j represents movement in the y direction (width) and k represents the movement in the z direction (depth)
- For example: The vector (-4i + 3j - k) would mean 4 units in the negative x direction, 3 units in the positive y direction and 1 unit in the negative z direction
- As they are vectors, i, j and k are displayed in bold in textbooks and online but in handwriting they would be underlined (i, j and k)
Exam Tip
- Practice working with all types of vector notation so that you are prepared for whatever comes up in the exam
- Your working and answer in the exam can be in any form unless told otherwise
- It is generally best to write your final answer in the same form as given in the question, however you will not lose marks for not doing this unless it is specified in the question
- Vectors appear in bold (non-italic) font in textbooks and on exam papers, etc (i.e. F, α ) but in handwriting should be underlined (i.e. F , α )
Worked Example


Parallel Vectors
How do you know if two vectors are parallel?
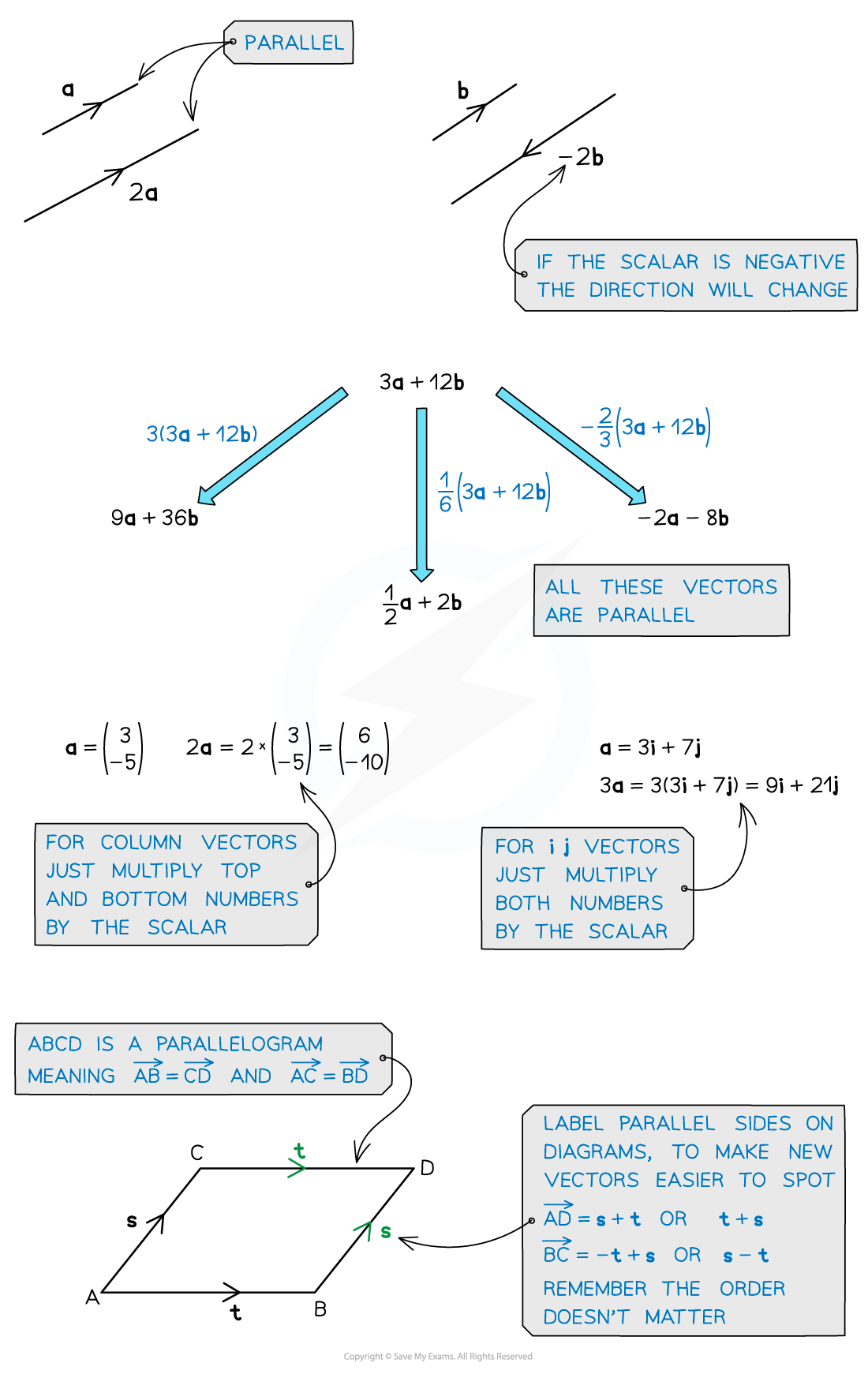
- Two vectors are parallel if one is a scalar multiple of the other
- This means that all components of the vector have been multiplied by a common constant (scalar)
- Multiplying every component in a vector by a scalar will change the magnitude of the vector but not the direction
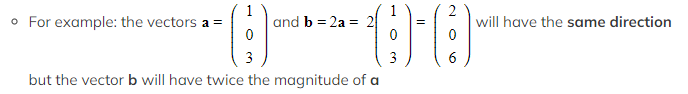
- They are parallel
- If a vector can be factorised by a scalar then it is parallel to any scalar multiple of the factorised vector
- For example: The vector 9i + 6j –3k can be factorised by the scalar 3 to 3(3i + 2j – k) so the vector 9i + 6j –3k is parallel to any scalar multiple of 3i + 2j – k
- If a vector is multiplied by a negative scalar its direction will be reversed
- It will still be parallel to the original vector
- Two vectors are parallel if they have the same or reverse direction and equal if they have the same size and direction
Exam Tip
- It is easiest to spot that two vectors are parallel when they are in column vector notation
- in your exam by writing vectors in column vector form and looking for a scalar multiple you will be able to quickly determine whether they are parallel or not
Worked Example
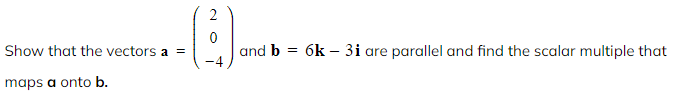

转载自savemyexams


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








