- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记3.7.2 Inverse Trig Functions
Inverse Trig Functions
What are the inverse trig functions?
- The functions arcsin, arccos and arctan are the inverse functions of sin, cos and tan respectively when their domains are restricted
- sin (arcsin x) = x for -1 ≤ x ≤ 1
- cos (arccos x) = x for -1 ≤ x ≤ 1
- tan (arctan x) = x for all x
- You will have seen and used the inverse trig operations many times already
- Arcsin is the operation sin-1
- Arccos is to the operation cos-1
- Arctan is the operation tan-1
- The domains of sin, cos, and tan must first be restricted to make them one-to-one functions
- A function can only have an inverse if it is a one-to-one function
- The domain of sin x is restricted to -π/2 ≤ x ≤ π/2 (-90° ≤ x ≤ 90°)
- The domain of cos x is restricted to 0 ≤ x ≤ π (0° ≤ x ≤ 180°)
- The domain of tan x is restricted to -π/2 < x < π/2 (-90° < x < 90°)
- Be aware that sin-1 x, cos-1 x, and tan-1 x are not the same as the reciprocal trig functions
- They are used to solve trig equations such as sin x = 0.5 for all values of x
- arcsin x is the same as sin-1 x but not the same as (sin x)-1
What do the graphs of the inverse trig functions look like?
- The graphs of arcsin, arccos and arctan are the reflections of the graphs of sin, cos and tan (after their domains have been restricted) in the line y = x
- The domains of arcsin x and arccos x are both -1 ≤ x ≤ 1
- The range of arcsin x is -π/2 ≤ y ≤ π/2
-
- The range of arccos x is 0 ≤ y ≤ π
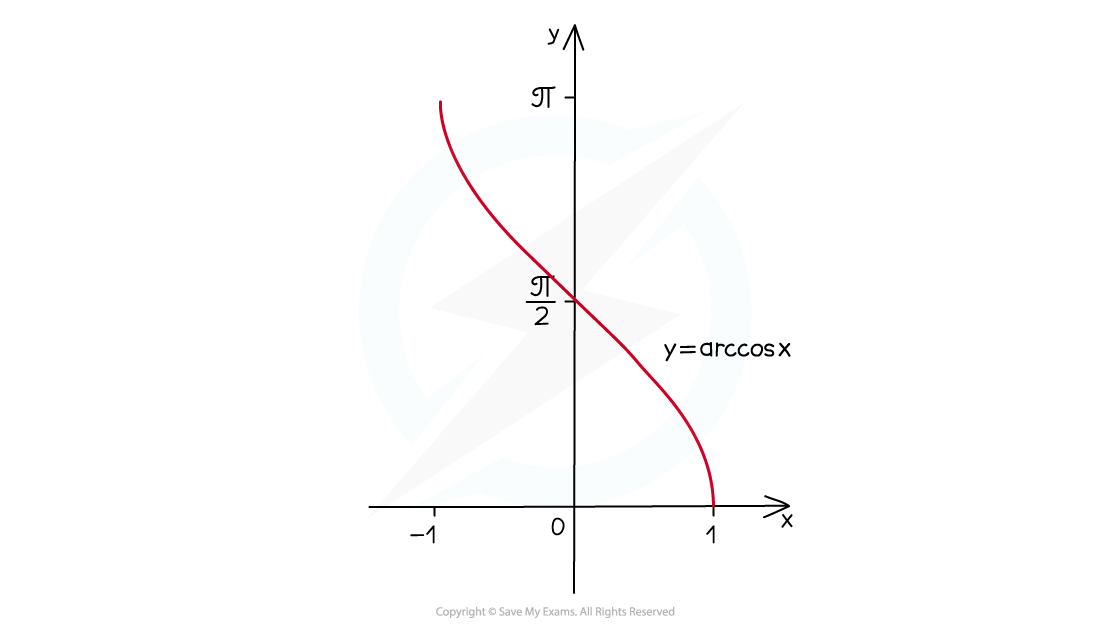
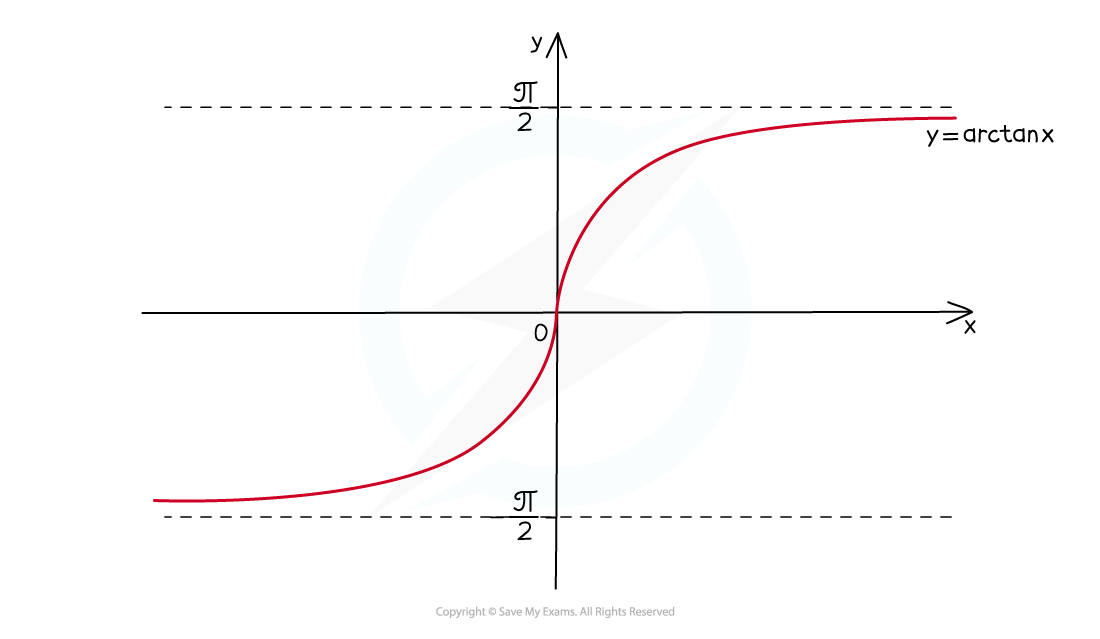
- The domain of arctan x is x ∈ ℝ
- The range of arctan x is -π/2 < y < π/2
- Note that there are horizontal asymptotes at π/2 and -π/2
How are the inverse trig functions used?
- The functions arcsin, arccos and arctan are used to evaluate trigonometric equations such as sin x = 0.5
- If sin x = 0.5 then arcsin 0.5 = x for values of x between -π/2 ≤ x ≤ π/2
- You can then use symmetries of the trig function to find solutions over other intervals
- If sin x = 0.5 then arcsin 0.5 = x for values of x between -π/2 ≤ x ≤ π/2
- The inverse trig functions are also used to help evaluate algebraic expressions
- From sin (arcsin x) = x we can also say that sinn(arcsin x) = xn for -1 ≤ x ≤ 1
- If using an inverse trig function to evaluate an algebraic expression then remember to consider the domain and range of the function
- arcsin(sin x) = x only for -π/2 ≤ x ≤ π/2
- arccos(cos x) = x only for 0 ≤ x ≤ π
- arctan(tan x) = x only for -π/2 < x < π/2
- The symmetries of the trig functions can be used when values lie outside of the domain or range
- Using sin(x) = sin(π - x) you get arcsin(sin(2π/3)) = arcsin(sin(π/3)) = π/3
Exam Tip
 Worked Example
Worked Example
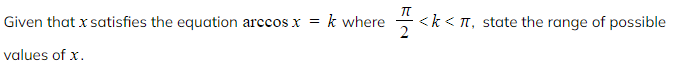
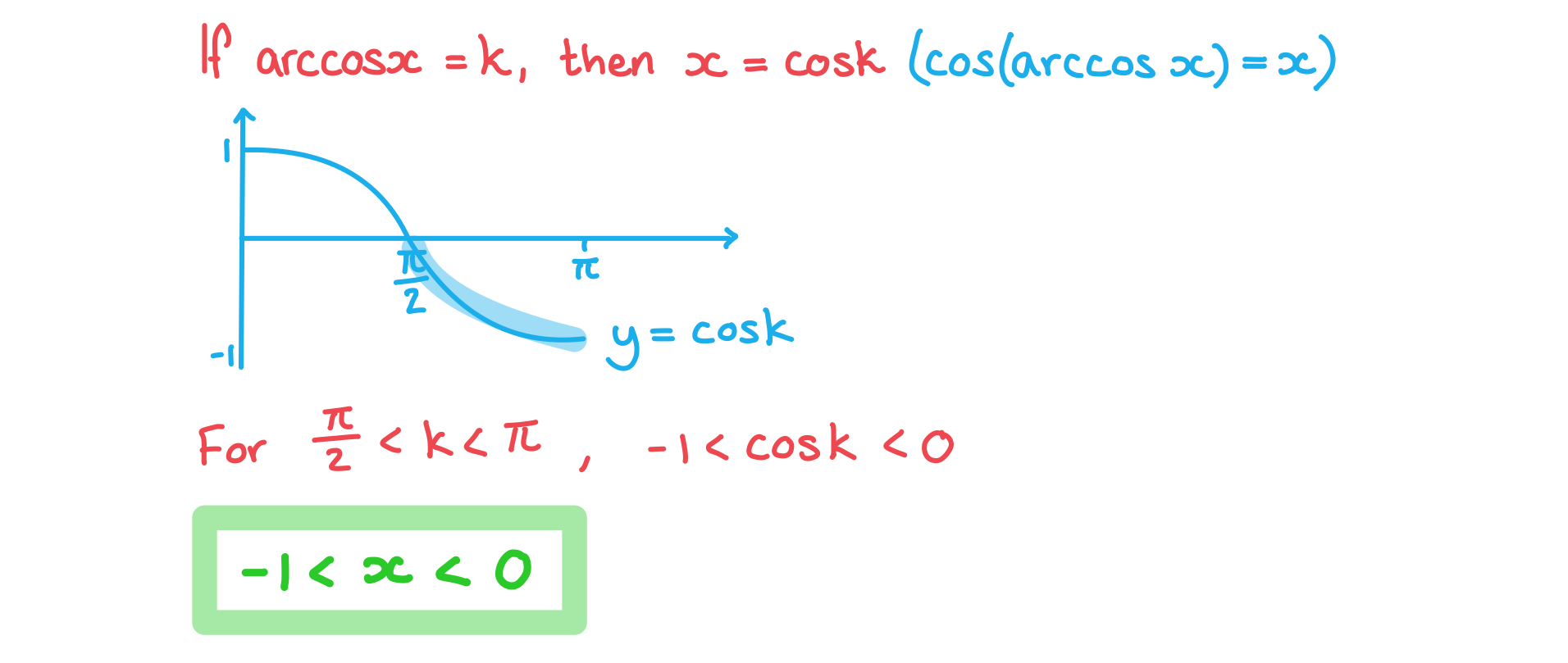
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








