- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记3.6.2 Compound Angle Formulae
Compound Angle Formulae
What are the compound angle formulae?
- There are six compound angle formulae (also known as addition formulae), two each for sin, cos and tan:
- For sin the +/- sign on the left-hand side matches the one on the right-hand side
- sin(A+B)≡sinAcosB + cosAsinB
- sin(A-B)≡sinAcosB - cosAsinB
- For cos the +/- sign on the left-hand side is opposite to the one on the right-hand side
- cos(A+B)≡cosAcosB - sinAsinB
- cos(A-B)≡cosAcosB + sinAsinB
- For tan the +/- sign on the left-hand side matches the one in the numerator on the right-hand side, and is opposite to the one in the denominator
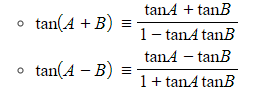 The compound angle formulae can all the found in the formula booklet, you do not need to remember them
The compound angle formulae can all the found in the formula booklet, you do not need to remember them
When are the compound angle formulae used?
- The compound angle formulae are particularly useful when find the values of trigonometric ratios without the use of a calculator
- For example to find the value of sin15° rewrite it as sin (45 – 30)° and then
- apply the compound formula for sin(A – B)
- use your knowledge of exact values to calculate the answer
- For example to find the value of sin15° rewrite it as sin (45 – 30)° and then
- The compound angle formulae are also used…
- … to derive further multiple angle trig identities such as the double angle formulae
- … in trigonometric proof
- … to simplify complicated trigonometric equations before solving
How are the compound angle formulae for cosine proved?
- The proof for the compound angle identity cos (A – B ) = cos A cos B + sin A sin B can be seen by considering two coordinates on a unit circle, P (cos A, sin A) and Q (cos B, sin B )
- The angle between the positive x- axis and the point P is A
- The angle between the positive x- axis and the point Q is B
- The angle between P and Q is B – A
- Using the distance formula (Pythagoras) the distance PQ can be given as
- |PQ|2 = (cos A – cos B)2 + (sin A – sin B)2
- Using the cosine rule the distance PQ can be given as
- |PQ|2 = 12 + 12 -2(1)(1)cos(B – A) = 2 - 2 cos(B – A)
- Equating these two formulae, expanding and rearranging gives
- 2 - 2 cos(B – A) = cos2A + sin2A + cos2B + sin2B –2 cos A cos B - 2sin A sin B
- 2 - 2 cos(B – A) = 2 – 2(cos A cos B + sin A sin B )
- Therefore cos (B – A) = cos A cos B + sin A sin B
- Changing -A for A in this identity and rearranging proves the identity for cos (A + B)
- cos (B – (-A)) = cos(-A) cos B + sin(-A) sin B = cos A cos B – sin A sin B
How are the compound angle formulae for sine proved?
- The proof for the compound angle identity sin (A + B ) can be seen by using the above proof for cos (B – A) and
- Considering cos (π/2 – (A + B)) = cos (π/2)cos(A + B) + sin(π/2)sin(A + B)
- Therefore cos (π/2 – (A + B)) = sin(A + B)
- Rewriting cos (π/2 – (A + B)) as cos ((π/2 – A) + B) gives
- cos (π/2 – (A + B)) = cos (π/2 – A) cos B + sin (π/2 – A) sin B
- Using cos (π/2 – A) = sin A and sin (π/2 – A) = cos A and equating gives
- sin (A + B) = sin A cos B + cos A cos B
- Substituting B for -B proves the result for sin (A – B)
How are the compound angle formulae for tan proved?
- The proof for the compound angle identities tan (A ± B) can be seen by
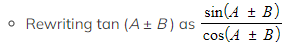 Substituting the compound angle formulae in
Substituting the compound angle formulae in- Dividing the numerator and denominator by cos A cos B
Exam Tip
- All these formulae are in the Topic 3: Geometry and Trigonometry section of the formula booklet – make sure that you use them correctly paying particular attention to any negative/positive signs
Worked Example
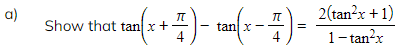

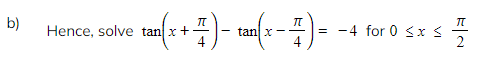

转载自savemyexams


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








