- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记1.10.2 Algebraic Solutions
How can I write a system of linear equations?
- To save space we can just write the coefficients without the variables

What is a row reduced system of linear equations?
- A system of linear equations is in row reduced form if it is written as:

- It is very helpful if the values of A1, B2, C3 are equal to 1
What are row operations?
-
- Row operations are used to make the linear equations simpler to solve
- They do not affect the solution
- Row operations are used to make the linear equations simpler to solve

How can I row reduce a system of linear equations?
How do I solve a system of linear equations once it is in row reduced form?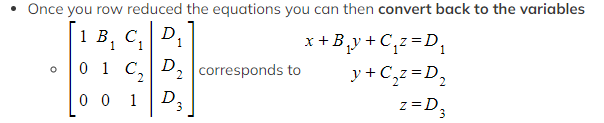
- Solve the equations starting at the bottom
- You have the value for z from the third equation
- Substitute z into the second equation and solve for y
- Substitute z and y into the first each and solve for x
Exam Tip
- To reduce the number of operations you do whilst solving a system of operations, you can do a couple of things:
- You can set up your original matrix with the equations in any order, so if one of the equations already has a 1 in the top left corner, put that one first
- You do not need to make every equation so that it only has a single variable with a value of 1, you just need to do that for 1 of the equations and use that result to work out the others
Worked Example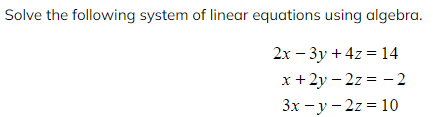

Number of Solutions to a System
How many solutions can a system of linear equations have?
- There could be
- 1 unique solution
- No solutions
- An infinite number of solutions
- You can determine the case by looking at the row reduced form
How do I know if the system of linear equations has no solutions?
- Systems with no solutions are called inconsistent
- When trying to solve the system after using the row reduction method you will end up with a mathematical statement which is never true:
- Such as: 0 = 1
- The row reduced system will contain:
- At least one row where the entries to the left of the line are zero and the entry on the right of the line is non-zero
- Such a row is called inconsistent
- For example:
- At least one row where the entries to the left of the line are zero and the entry on the right of the line is non-zero
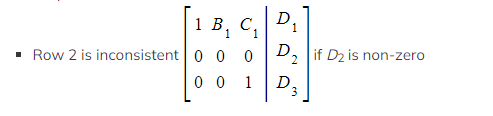 How do I know if the system of linear equations has infinite solutions?
How do I know if the system of linear equations has infinite solutions?
- Systems with at least one solution are called consistent
- The solution could be unique or there could be an infinite number of solutions
- When trying to solve the system after using the row reduction method you will end up with a mathematical statement which is always true
- Such as: 0 = 0
- The row reduced system will contain:
- At least one row where all the entries are zero
- No inconsistent rows
- For example:
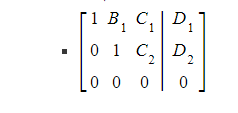 How do I find the general solution of a dependent system?
How do I find the general solution of a dependent system?
- A dependent system of linear equations is one where there are infinite number of solutions
- The general solution will depend on one or two parameters
- In the case where two rows are zero
- Let the variables corresponding to the zero rows be equal to the parameters λ & μ
- For example: If the first and second rows are zero rows then let x = λ & y = μ
- Find the third variable in terms of the two parameters using the equation from the third row
- For example: z = 4λ – 5μ + 6
- Let the variables corresponding to the zero rows be equal to the parameters λ & μ
- In the case where only one row is zero
- Let the variable corresponding to the zero row be equal to the parameter λ
- For example: If the first row is a zero row then let x = λ
- Find the remaining two variables in terms of the parameter using the equations formed by the other two rows
- For example: y = 3λ – 5 & z = 7 – 2λ
- Let the variable corresponding to the zero row be equal to the parameter λ
Exam Tip
- Common questions that pop up in an IB exam include questions with equations of lines
- Being able to recognise whether there are no solutions, 1 solution or infinite solutions is really useful for identifying if lines are coincident, skew or intersect!
Worked Example
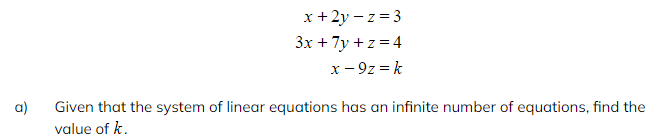

b) Find a general solution to the system.

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








