IB DP Maths: AA HL复习笔记1.9.5 Roots of Complex Numbers
How do I find the square root of a complex number?
-
- The square roots of a complex number will themselves be complex:
How do I use de Moivre’s Theorem to find roots of a complex number?
- De Moivre’s Theorem states that a complex number in modulus-argument form can be raised to the power of n by
- Raising the modulus to the power of n and multiplying the argument by n
- When in modulus-argument (polar) form de Moivre’s Theorem can then be used to find the roots of a complex number by
- Taking the nth root of the modulus and dividing the argument by n
-
- The five roots of a complex number raised to the power 5 will create a regular pentagon on an Argand diagram
- The eight roots of a complex number raised to the power 8 will create a regular octagon on an Argand diagram
- The n roots of a complex number raised to the power n will create a regular n-sided polygon on an Argand diagram
- Taking the nth root of the modulus and dividing the argument by n
- Sometimes you may need to use your GDC to find the roots of a complex number
- Using your GDC’s store function will help when entering complicated modulus and arguments
- Make sure you choose the correct form to enter your complex number in
- Your GDC should be able to give you the answer in your preferred form
Exam Tip
- De Moivre's theorem makes finding roots of complex numbers very easy, but you must be confident converting from Cartesian form into Polar and Euler's form first
- If you are in a calculator exam your GDC will be able to do this for you but you must clearly show how you got to your answer
- You must also be prepared to do this by hand in a non-calculator paper
Worked Example
a) Find the square roots of 5 + 12i, giving your answers in the form a + bi.
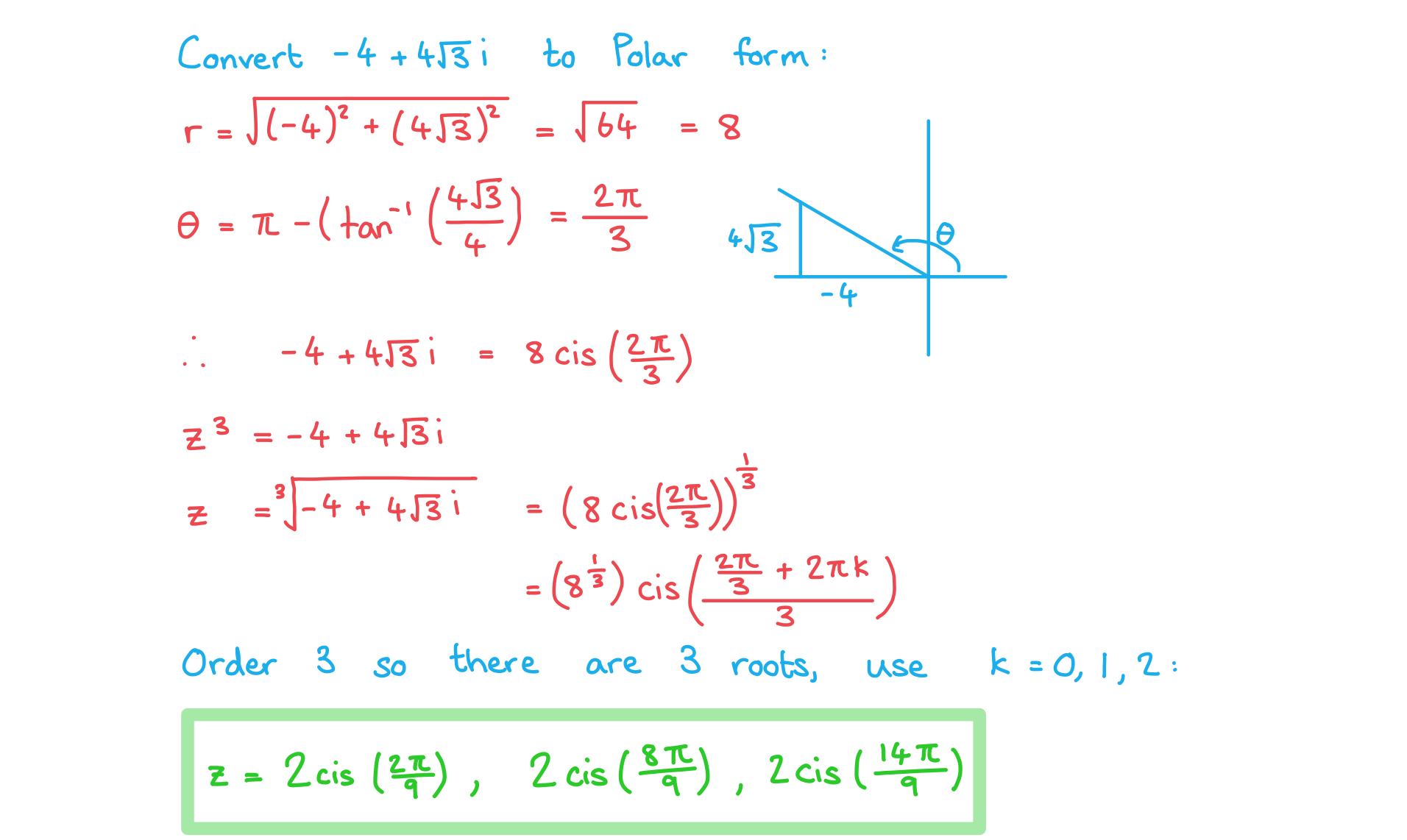
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
