IB DP Maths: AA HL复习笔记1.9.3 Complex Roots of Polynomials

What are complex roots?

• A quadratic equation can either have two real roots (zeros), a repeated real root or no real roots
  • This depends on the location of the graph of the quadratic with respect to the x-axis
• If a quadratic equation has no real roots we would previously have stated that it has no real solutions
  • The quadratic equation will have a negative discriminant
  • This means taking the square root of a negative number
• Complex numbers provide solutions for quadratic equations that have no real roots

How do we solve a quadratic equation when it has complex roots?

• If a quadratic equation takes the form ax² + bx + c = 0 it can be solved by either using the quadratic formula or completing the square
• If a quadratic equation takes the form ax² + b = 0 it can be solved by rearranging
• The property i = √-1 is used
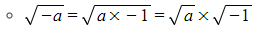• If the coefficients of the quadratic are real then the complex roots will occur in complex conjugate pairs
  • If z = m + ni (n ≠ 0) is a root of a quadratic with real coefficients then z* = m - ni is also a root
• The real part of the solutions will have the same value as the x coordinate of the turning point on the graph of the quadratic

• When the coefficients of the quadratic equation are non-real, the solutions will not be complex conjugates
  • To solve these you can use the quadratic formula

How do we factorise a quadratic equation if it has complex roots?

• If we are given a quadratic equation in the form az² + bz + c = 0, where a, b, and c ∈ ℝ, a ≠ 0 we can use its complex roots to write it in factorised form
  • Use the quadratic formula to find the two roots, z  = p + qi and z* = p - qi
  • This means that z – (p + qi) and z – (p – qi) must both be factors of the quadratic equation
  • Therefore we can write az² + bz + c = (z – (p + qi))( z – (p - qi))
  • This can be rearranged into the form (z – p – qi)(z – p + qi)

How do we find a quadratic equation when given a complex root?

• If we are given a complex root in the form z = p + qi we can find the quadratic equation in the form az² + bz + c = 0, where a, b, and c ∈ ℝ, a ≠ 0
  • We know that the second root must be z* = p - qi
  • This means that z – (p + qi) and z – (p – qi) must both be factors of the quadratic equation
  • Therefore we can write az² + bz + c = (z – (p + qi))( z – (p - qi))
  • Rewriting this as ((z – p) – qi))((z – p) + qi)) makes expanding easier
  • Expanding this gives the quadratic equation z² – 2pz + (p² + q²)
    • a = 1
    • b = -2p
    • c = p² + q²
• This demonstrates the important property (x – z)(x – z*) = x² - 2Re(z)x + |z|²

How many roots should a polynomial have?

• We know that every quadratic equation has two roots (not necessarily distinct or real)
• This is a particular case of a more general rule:
  • Every polynomial equation, with real coefficients, of degree n has n roots
  • The n roots are not necessarily all distinct and therefore we need to count any repeated roots that may occur individually
• From the above rule we can state the following:
  • 3 real roots
    • Or 1 real root and a complex conjugate pair

• 
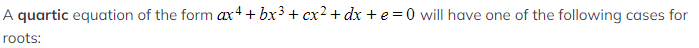
  • 4 real roots
  • 2 real and 2 nonreal (a complex conjugate pair)
  • 4 nonreal (two complex conjugate pairs)

• When a polynomial of any degree has one complex root it will always also have the complex conjugate as a root

How do we solve a cubic equation with complex roots?

• Steps to solve a cubic equation with complex roots
  • If we are told thatp + qi is a root, then we know p - qi is also a root
  • This means that z – (p + qi) and z – (p – qi) must both be factors of the cubic equation
  • Multiplying the above factors together gives us a quadratic factor of the form (Az² + Bz + C)
  • We need to find the third factor (z - α)
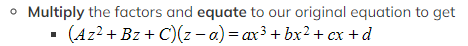  • From there either
    • Expand and compare coefficients to find
    • Or use polynomial division to find the factor (z - α)
  • Finally, write your three roots clearly

How do we solve a polynomial of any degree with complex roots?

• When asked to find the roots of any polynomial when we are given one, we use almost the same method as for a cubic equation
  • State the initial root and its conjugate and write their factors as a quadratic factor (as above) we will have two unknown roots to find, write these as factors (z - α) and (z - β)
  • The unknown factors also form a quadratic factor (z - α)(z - β)
  • Then continue with the steps from above, either comparing coefficients or using polynomial division
    • If using polynomial division, then solve the quadratic factor you get to find the roots α and β

How do we solve polynomial equations with unknown coefficients?

• Steps to find unknown variables in a given equation when given a root:
  • Substitute the given root p + qi into the equation f(z) = 0
  • Expand and group together the real and imaginary parts (these expressions will contain our unknown values)
  • Solve as simultaneous equations to find the unknowns
  • Substitute the values into the original equation
  • From here continue using the previously described methods for finding other roots for the polynomial

How do we factorise a polynomial when given a complex root?

• If we are given a root of a polynomial of any degree in the form z = p + qi
  • We know that the complex conjugate, z*= p – qi is another root
  • We can write (z – (p + qi)) and ( z – (p - qi)) as two linear factors
    • Or rearrange into one quadratic factor
  • This can be multiplied out with another factor to find further factors of the polynomial
• For higher order polynomials more than one root may be given
  • If the further given root is complex then its complex conjugate will also be a root
  • This will allow you to find further factors