IB DP Maths: AA HL复习笔记1.6.2 Extension of The Binomial Theorem
How do I use the binomial theorem for fractional and negative indices?
How do we use the binomial theorem to estimate a value?
- The binomial expansion can be used to form an approximation for a value raised to a power
-
- Check that the value of x is within the interval of convergence for the expression
- If x is outside the interval of convergence then the approximation may not be valid
Exam Tip
- Students often struggle with the extension of the binomial theorem questions in the exam, however the formula is given in the formula booklet
- Make sure you can locate the formula easily and practice substituting values in
- Mistakes are often made with negative numbers or by forgetting to use brackets properly
- Writing one term per line can help with both of these
Worked Example
a) Write down the first three terms.
b) State the interval of convergence for the complete expansion.
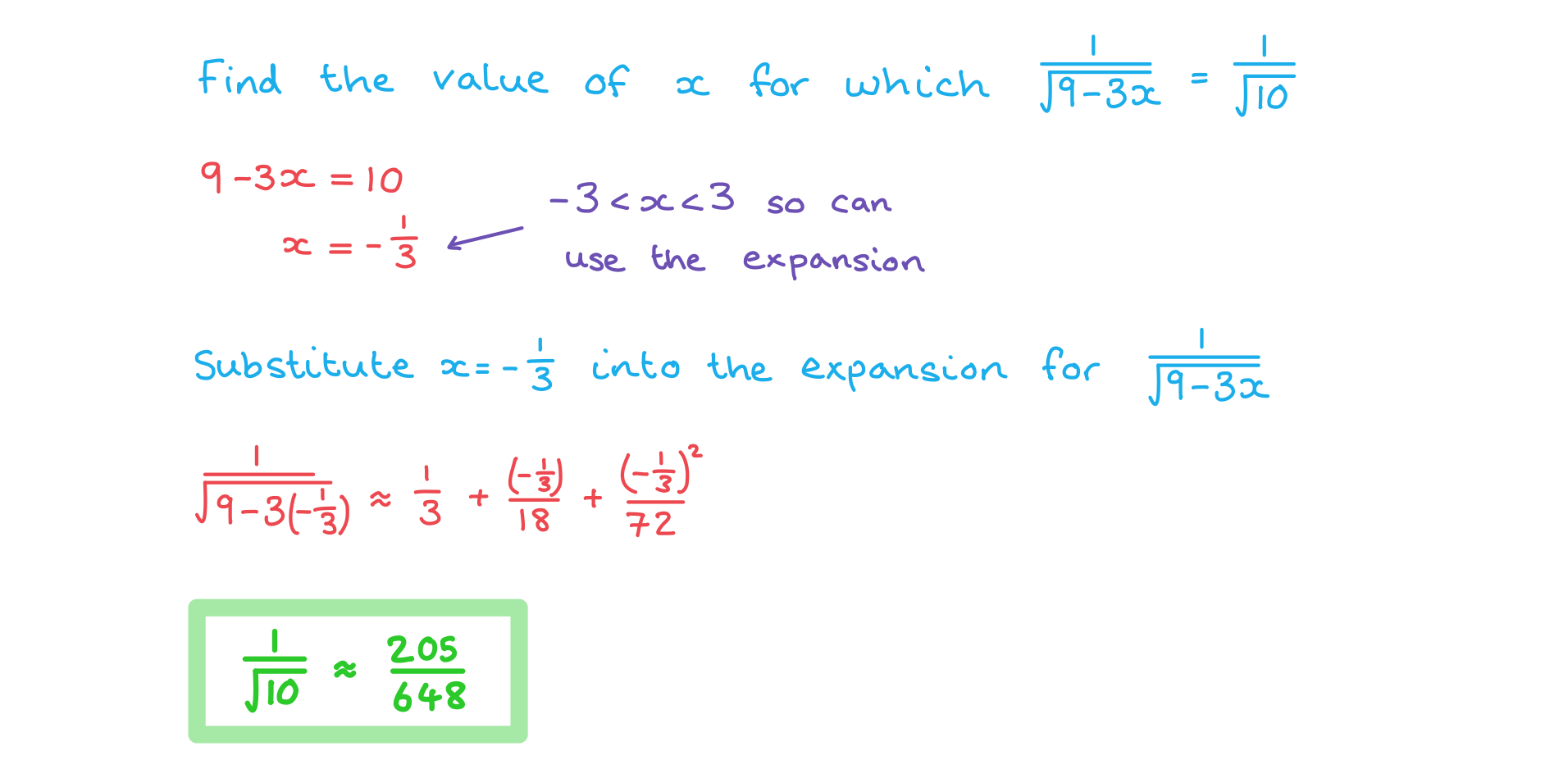
转载自savemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
