- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AA HL复习笔记1.1.3 Partial Fractions
What are partial fractions?
- Partial fractions allow us to simplify rational expressions into the sum of two or more fractions with constant numerators and linear denominators
- This allows for integration of rational functions
- The method of partial fractions is essentially the reverse of adding or subtracting fractions
- When adding fractions, a common denominator is required
- In partial fractions the common denominator is split into parts (factors)
- If we have a rational function with a quadratic on the denominator partial fractions can be used to rewrite it as the sum of two rational functions with linear denominators
- This works if the non-linear denominator can be factorised into two distinct factors
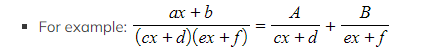 If we have a rational function with a linear numerator and denominator partial fractions can be used to rewrite it as the sum of a constant and a fraction with a linear denominator
If we have a rational function with a linear numerator and denominator partial fractions can be used to rewrite it as the sum of a constant and a fraction with a linear denominator
- The linear denominator does not need to be factorised
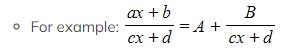 How do I find partial fractions if the denominator is a quadratic?
How do I find partial fractions if the denominator is a quadratic?
 How do I find partial fractions if the numerator and denominator are both linear?
How do I find partial fractions if the numerator and denominator are both linear?
- If the denominator is not a quadratic expression you will be given the form in which the partial fractions should be expressed
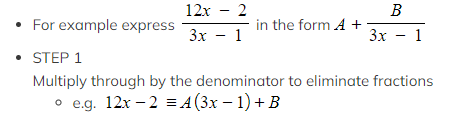 STEP 2
STEP 2
Expand the expression on the right-hand side and compare coefficients- Compare the coefficients of x and solve for the first unknown
- e.g. 12x = 3Ax
- therefore A = 4
- Compare the constant coefficients and solve for the second unknown
-
- e.g. - 2 = - A + B = - 4 + B
- therefore B = 2
-
- Compare the coefficients of x and solve for the first unknown
- STEP 3
Write the original as partial fractions
How do I find partial fractions if the denominator has a squared linear term?
- A squared linear factor in the denominator actually represents two factors rather than one
- This must be taken into account when the rational function is split into partial fractions
- For the squared linear denominator (ax + b)2 there will be two factors: (ax + b) and (ax + b)2
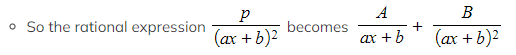 In IB you will be given the form into which you should split the partial fractions
In IB you will be given the form into which you should split the partial fractions
- Put the rational expression equal to the given form and then continue with the steps above
- There is more than one way of finding the missing values when working with partial fractions
- Substituting values is usually quickest, however you should look at the number of times a bracket is repeated to help you decide which method to use
Exam Tip
- An exam question will often have partial fractions as part (a) and then integration or using the binomial theorem as part (b)
- Make sure you use your partial fractions found in part (a) to answer the next part of the question
Worked Example
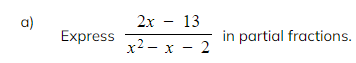



转载自savemyexams

在线登记
最新发布
翰林课程体验,退费流程快速投诉邮箱: yuxi@linstitute.net 沪ICP备2023009024号-1








