USACO 2020 US Open Contest, Gold Problem 2. Favorite Colors

USACO 2020 US Open Contest, Gold Problem 2. Favorite Colors

Each of Farmer John's NN cows (1≤N≤2⋅1051≤N≤2⋅105) has a favorite color. The cows are conveniently labeled 1…N1…N (as always), and each color can be represented by an integer in the range 1…N1…N.

There exist MM pairs of cows (a,b)(a,b) such that cow bb admires cow aa (1≤M≤2⋅1051≤M≤2⋅105). It is possible that a=ba=b, in which case a cow admires herself. For any color cc, if cows xx and yy both admire a cow with favorite color cc, then xx and yy share the same favorite color.

Given this information, determine an assignment of cows to favorite colors such that the number of distinct favorite colors among all cows is maximized. As there are multiple assignments that satisfy this property, output the lexicographically smallest one (meaning that you should take the assignment that minimizes the colors assigned to cows 1…N1…N in that order).

 

 

 

SAMPLE INPUT:

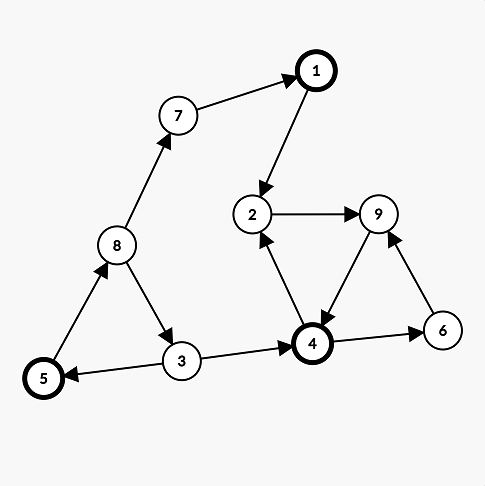
9 12
1 2
4 2
5 8
4 6
6 9
2 9
8 7
8 3
7 1
9 4
3 5
3 4

SAMPLE OUTPUT:

1
2
3
1
1
2
3
2
3

In the image below, the circles with bolded borders represent the cows with favorite color 1.

 

 

Problem credits: William Lin and Benjamin Qi

USACO 2020 US Open Contest, Gold Problem 2. Favorite Colors 题解(翰林国际教育提供，仅供参考)

题解请注册或登录查看

[/hide]

(Analysis by Benjamin Qi)

If both cows bb and cc admire cow aa then both bb and cc must have the same color. From now on, we can treat both bb and cc as the same cow; change all occurrences of cc to bb and merge the adjacency list of cc into that of bb. Repeat this process while at least two distinct cows admire the same cow.

Once we reach a configuration in which a cow is admired by at most one cow this process terminates; we can just assign every cow a distinct color. If we always merge the smaller adjacency list of the two cows into the larger one then our solution runs in O((N+M)logN)O((N+M)log⁡N) time. We ensured that a few slow solutions did not pass but it is likely that many (not necessarily provable) heuristics passed anyways.

 

#include <bits/stdc++.h>
using namespace std;
 
void setIO(string s) {
	ios_base::sync_with_stdio(0); cin.tie(0); 
	freopen((s+".in").c_str(),"r",stdin);
	freopen((s+".out").c_str(),"w",stdout);
}
 
const int MX = 2e5+5;
 
int N,M;
 
int par[MX],cnt[MX];
vector<int> adj[MX], rpar[MX];
queue<int> q; 
 
void merge(int a, int b) {
	a = par[a], b = par[b]; 
	if (rpar[a].size() < rpar[b].size()) swap(a,b);
	for (int t: rpar[b]) { par[t] = a; rpar[a].push_back(t); }
	adj[a].insert(end(adj[a]),begin(adj[b]),end(adj[b])); 
	adj[b].clear();
	if (adj[a].size() > 1) q.push(a);
}
 
int main() { 
	setIO("fcolor");
	cin >> N >> M;
	for (int i = 0; i < M; ++i) {
		int a,b; cin >> a >> b;
		adj[a].push_back(b);
	}
	for (int i = 1; i <= N; ++i) {
		par[i] = i; rpar[i].push_back(i);
		if (adj[i].size() > 1) q.push(i);
	}
	while (q.size()) {
		int x = q.front(); if (adj[x].size() <= 1) { q.pop(); continue; }
		int a = adj[x].back(); adj[x].pop_back();
		if (par[a] == par[adj[x].back()]) continue;
		merge(a,adj[x].back());
	}
	int co = 0;
	for (int i = 1; i <= N; ++i) {
		if (!cnt[par[i]]) cnt[par[i]] = ++co;
		cout << cnt[par[i]] << "n";
	}
}

[/hide]