- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2021 December Contest, Gold Problem 3. Bracelet Crossings
USACO 2021 December Contest, Gold Problem 3. Bracelet Crossings
Bessie the cow enjoys arts and crafts. In her free time, she has made NN (1≤N≤501≤N≤50) bracelets, conveniently numbered 1…N1…N. The iith bracelet is painted color ii out of a set of NN different colors. After constructing the bracelets, Bessie placed them on a table for display (which we can think of as the 2D plane). She was careful to arrange the bracelets to satisfy the following three conditions:
- Every bracelet was a single closed polygonal chain -- a series of vertices (points) connected sequentially by line segments, where the first and last points are the same (Feel welcome to consult the wikipedia page for more detail: polygonal chain),
- No bracelet intersected itself (this corresponds to a "simple" polygonal chain); and
- No two bracelets intersected.
Unfortunately, right after Bessie arranged the bracelets in such a careful manner, Farmer John drove by in his tractor, shaking the table and causing the bracelets to shift around and possibly break into multiple (not necessarily closed or simple) polygonal chains! Afterward, Bessie wanted to check whether the three conditions above still held. However, it was dark, so she couldn't see the bracelets anymore.
Fortunately, Bessie had a flashlight. She chose MM (1≤M≤501≤M≤50) vertical lines x=1,x=2,…,x=Mx=1,x=2,…,x=M and for each line, she swept the beam of the flashlight along that line from y=−∞y=−∞ to y=∞y=∞, recording the colors of all bracelets she saw in the order they appeared. Luckily, no beam crossed over any vertex of any polygonal chain or two line segments at the same time. Furthermore, for each beam, every color that appeared appeared exactly twice.
Can you help Bessie use this information to determine whether it is possible that the bracelets still satisfy all three of the conditions above?
INPUT FORMAT (input arrives from the terminal / stdin):
Each input case contains TT sub-cases (1≤T≤501≤T≤50) that must all solved independently to solve the full input case. Consecutive test cases are separated by newlines.The first line of the input contains TT. Each of the TT sub-test cases then follow.
The first line of each sub-test case contains two integers NN and MM. Each sub-test case then contains MM additional lines. For each ii from 11 to MM, the ii-th additional line contains an integer kiki (0≤ki≤2N0≤ki≤2N, kiki even), followed by kiki integers ci1,ci2,…,cikici1,ci2,…,ciki (cij∈[1,N]cij∈[1,N], every cijcij appears zero or two times). This means that when Bessie swept her flashlight from (i,−∞)(i,−∞) to (i,∞)(i,∞), she encountered the colors ci1,ci2,…,cikici1,ci2,…,ciki in that order.
OUTPUT FORMAT (print output to the terminal / stdout):
For each sub-test case, print YES if it is possible for the three conditions above to be satisfied. Otherwise, print NO.
SAMPLE INPUT:
5 1 2 2 1 1 2 1 1 1 3 2 1 1 0 2 1 1 2 1 4 1 2 1 2 4 2 6 1 2 2 3 3 1 6 1 2 4 4 2 1 2 2 4 1 1 2 2 4 2 2 1 1
SAMPLE OUTPUT:
YES NO NO YES NO
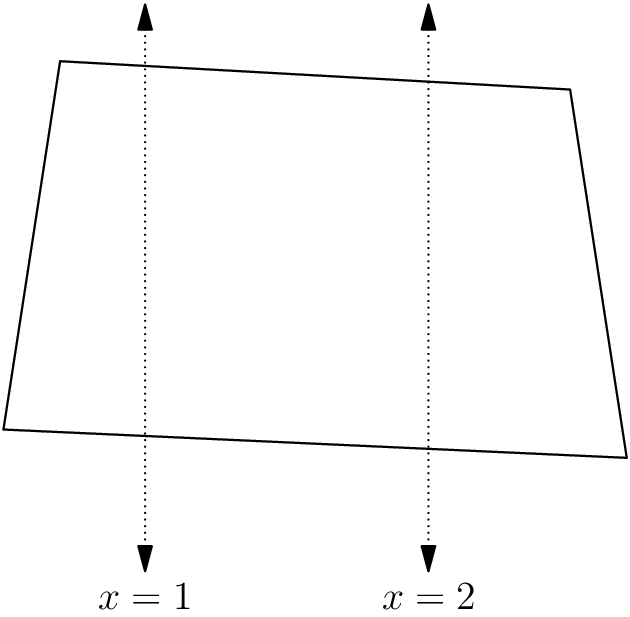
An example of a feasible bracelet configuration for the first sub-case is:
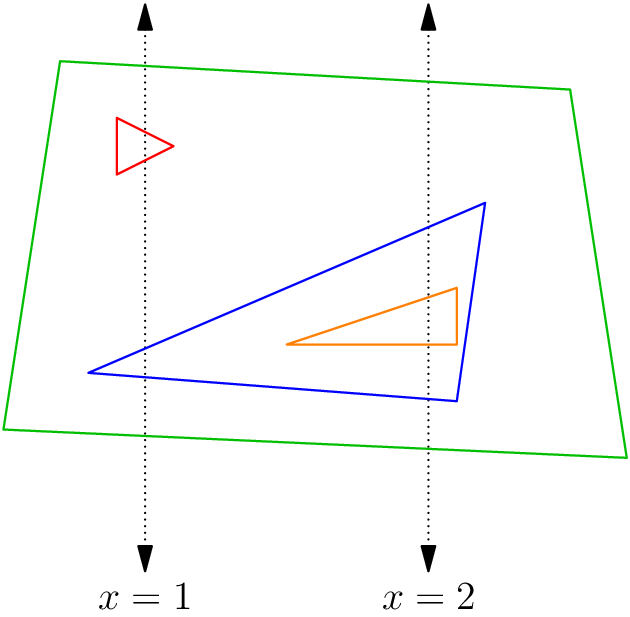
For the fourth sub-case, a feasible arrangement is the following:
SCORING:
- Test case 2 satisfies N=1N=1.
- Test cases 3-5 satisfy N=2N=2.
- Test cases 6-8 satisfy M=1M=1.
- Test cases 9-14 satisfy M=2M=2.
- Test cases 15-20 satisfy no additional constraints.
Problem credits: Richard Qi
USACO 2021 December Contest, Gold Problem 3. Bracelet Crossings 题解(翰林国际教育提供,仅供参考)
[/hide]
(Analysis by Andi Qu)
For each sub-case, we need to check 4 conditions:
Condition 1: Every color appears in a contiguous range of xx's.
We can check this condition by maintaining an array that describes at which xx a color last appeared. If the last xx is always 1 less than the current xx, then this condition holds.
Sub-case 2 in the example does not satisfy this condition.
Condition 2: For each xx, if one appearance of color aa is after the first appearance and before the second appearance of color bb, then the other appearance of color aa must do the same.
Let's say that a color becomes "activated" when it appears for the first time, and then "deactivated" when it appears the second time. We can then check this condition by maintaining a stack of active colors. When a color becomes deactivated, it must be at the top of the stack. If this is always true, then this condition holds.
Sub-case 3 in the example does not satisfy this condition.
If the 2 appearances of color aa are between the 2 appearances of color bb, then we know that bracelet aa must be contained inside bracelet bb. This hierarchical relationship allows us to transform the bracelets into a tree structure, where:
- The nodes are the bracelets.
- If a bracelet is contained by another bracelet, then its parent is the innermost bracelet that contains it.
- Otherwise, its parent is a placeholder node (e.g. node 00).
Condition 3: Each node's parent in the tree must be consistent for every xx it appears in.
This is because if some color appears, then its parent must also appear. We can check this condition by maintaining an array describing the parents of colors we've seen before. We can then check this array against the input for each xx.
Condition 4: The ordering of colors in the input must be consistent for every xx it appears in.
We can check this condition by maintaining 2 lists – one for the current xx's color order and the other for all previous xx's' color order. To check the ordering, we can compare the ordering of these two lists' intersection, and then merge the lists after processing xx by using 2 pointers. Since the constraints are so small, straightforward list insertion is fast enough for this.
Sub-case 5 in the example does not satisfy this condition.
Andi's code (which runs in O(N2M)O(N2M) time).
#include <algorithm>
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
int main() {
cin.tie(0)->sync_with_stdio(0);
int t, last_appeared[51], parent[51];
cin >> t;
while (t--) {
int n, m;
bool good = true;
vector<int> glob_order;
cin >> n >> m;
for (int i = 0; i <= n; i++) last_appeared[i] = parent[i] = -1;
while (m--) {
int k, curr = 0;
cin >> k;
stack<int> stck;
vector<int> curr_order;
while (k--) {
int c;
cin >> c;
if (!good) continue;
if (last_appeared[c] == m && stck.top() == c) {
stck.pop();
curr = parent[curr];
} else {
if ((~last_appeared[c] && last_appeared[c] != m + 1) ||
last_appeared[c] == m ||
(~last_appeared[c] && parent[c] != curr)) {
// Conditions 1, 2, and 3
good = false;
continue;
}
// Condition 4 part A
curr_order.push_back(c);
parent[c] = curr;
last_appeared[c] = m;
stck.push(c);
curr = c;
}
}
// Condition 4 part B
if (!good) continue;
int ptr = 0;
for (int i : curr_order) {
while (ptr != glob_order.size() &&
!count(curr_order.begin(), curr_order.end(), glob_order[ptr]))
ptr++;
if (!count(glob_order.begin(), glob_order.end(), i))
glob_order.insert(glob_order.begin() + ptr, i);
else if (ptr == glob_order.size() || glob_order[ptr] != i) {
good = false;
break;
}
ptr++;
}
}
cout << (good ? "YESn" : "NOn");
}
return 0;
}
Of course, it is possible to solve this problem in O(NM)O(NM) time, but it was not necessary to do so due to the low constraints.
[/hide]

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









