AQA A Level Chemistry复习笔记5.1.3 Born-Haber Calculations

• Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlattꝋ) by applying Hess’s law and rearranging:

ΔHfꝋ = ΔHatꝋ + ΔHatꝋ + IE + EA + ΔHlattꝋ

• If we simplify this into three terms, this makes the equation easier to see:
  • ΔHlattꝋ
  • ΔHfꝋ
  • ΔH1ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)

   

• The simplified equation becomes

ΔHfꝋ = ΔH1ꝋ + ΔHlattꝋ

So, if we rearrange to calculate the lattice energy, the equation becomes

ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ

• When calculating the ΔHlattꝋ, all other necessary values will be given in the question
• A Born-Haber cycle could be used to calculate any stage in the cycle
  • For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
  • The principle would be exactly the same
  • Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
  • Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value

   

• Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
  • For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
  • Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl- ions

   

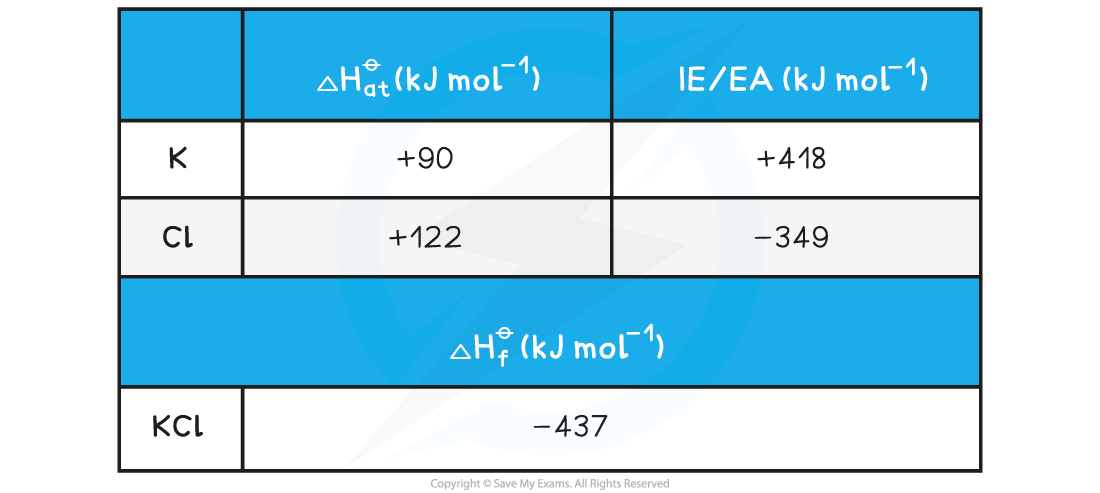
Answer

Step 1: The corresponding Born-Haber cycle is:

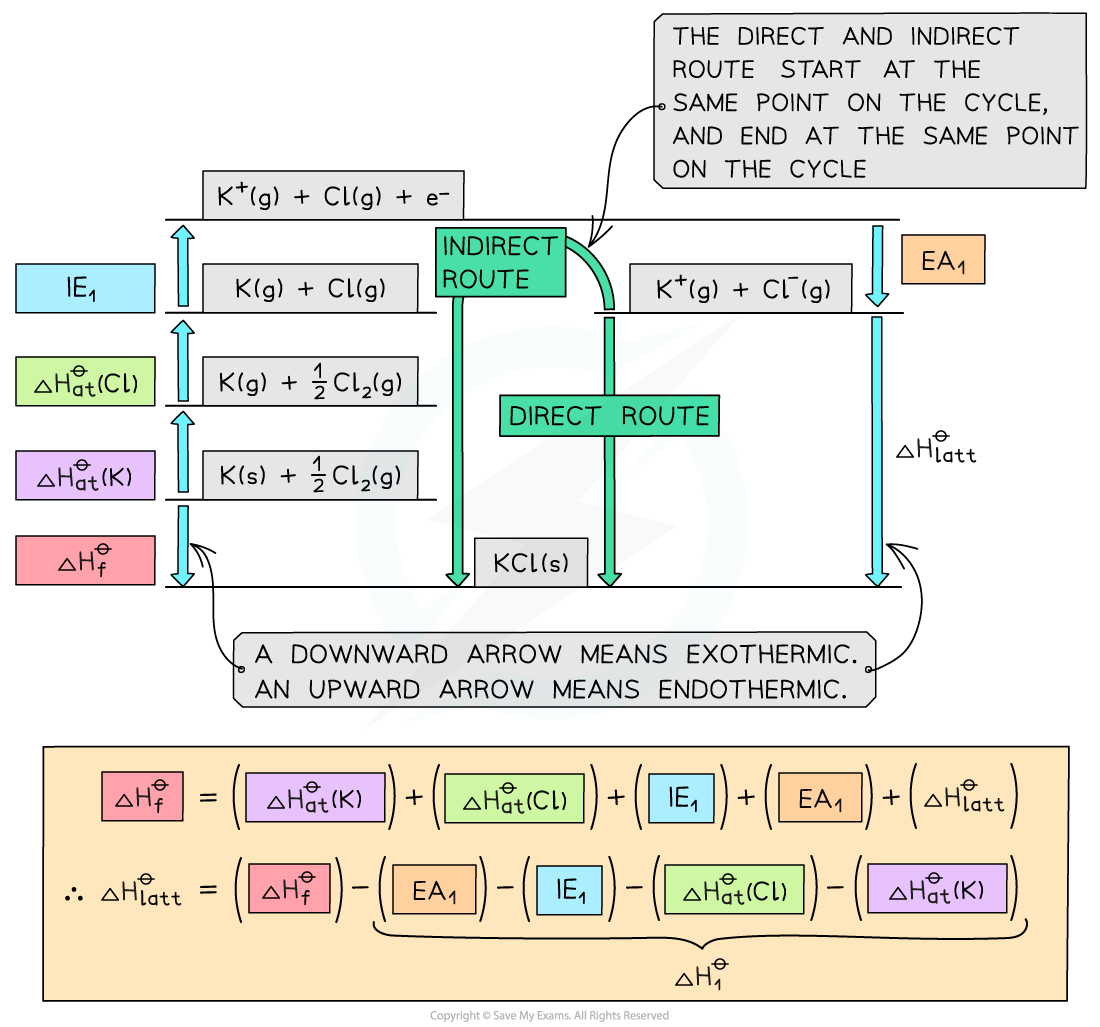
Step 2: Applying Hess’ law, the lattice energy of KCl is:

ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ

ΔHlattꝋ = ΔHfꝋ - [(ΔHatꝋ K) + (ΔHatꝋ Cl) + (IE1 K) + (EA1 Cl)]

Step 3: Substitute in the numbers:

ΔHlattꝋ = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol-1

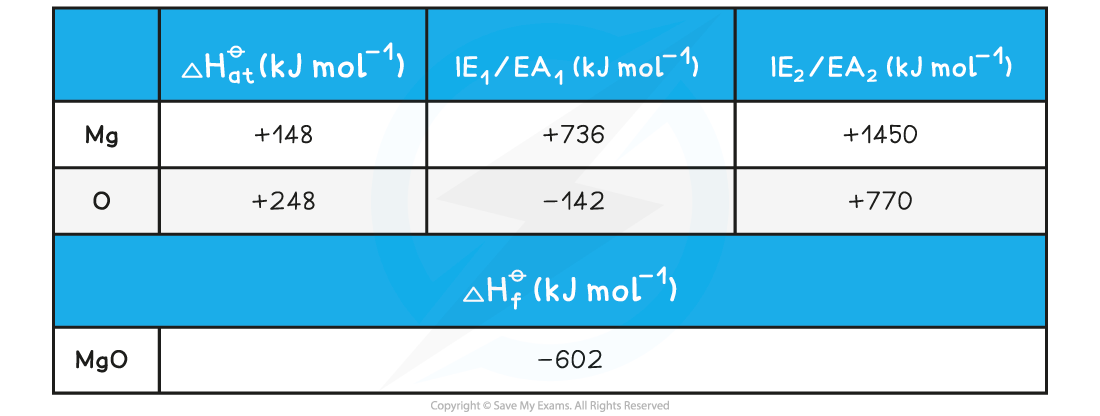
Answer

Step 1: The corresponding Born-Haber cycle is:

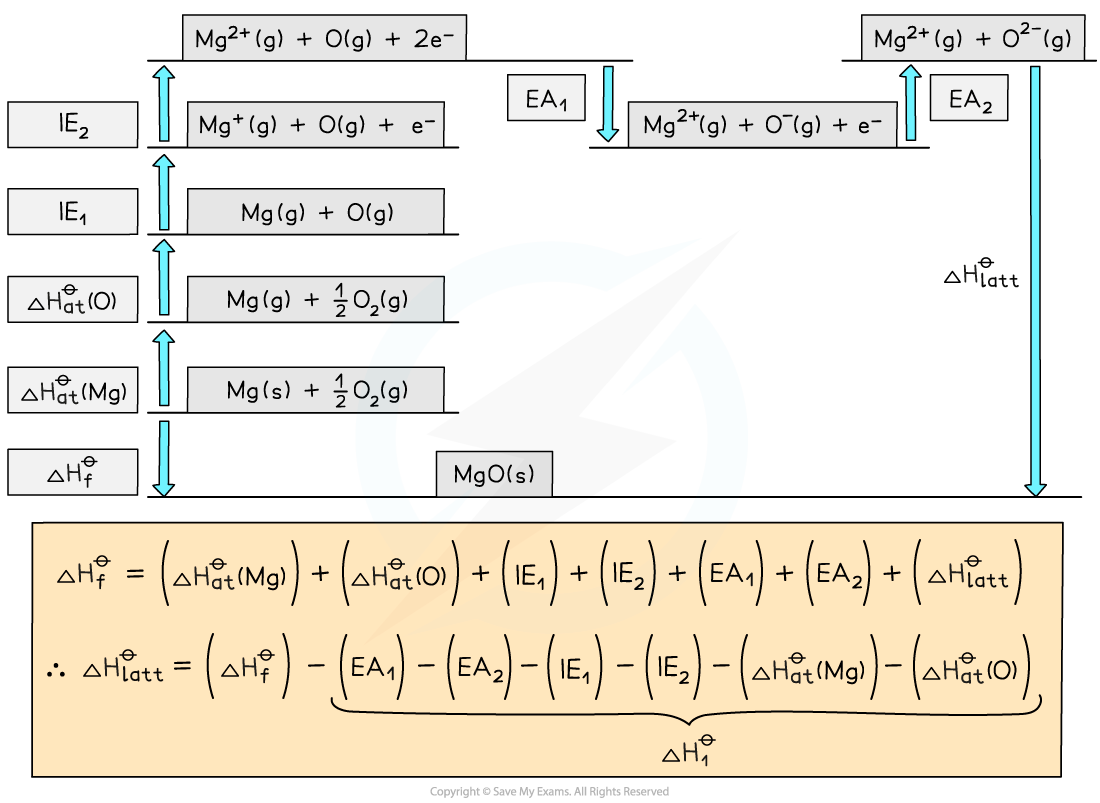
Step 2: Applying Hess’ law, the lattice energy of MgO is:

ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ

ΔHlattꝋ = ΔHfꝋ - [(ΔHatꝋ Mg) + (ΔHatꝋ O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]

Step 3: Substitute in the numbers:

ΔHlattꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]

= -3812 kJ mol-1