Edexcel IGCSE Maths 复习笔记 2.16.2 Solving Inequalities - Quadratic
Edexcel IGCSE Maths 复习笔记 2.16.2 Solving Inequalities - Quadratic
What is a quadratic inequality?
- An Inequality tells you that one expression is greater than (“>”) or less than (“<”) another
- “⩾” means “greater than or equal to”
- “⩽” means “less than or equal to”
- A Quadratic Inequality has an x2 (or a y2 etc) in it
- For example, 3x2 + 4x ⩾ 7 would be read “3x2 + 4x is greater than or equal to 7”
Solving quadratic inequalities
- Solving quadratic inequalities requires you to be able to factorise quadratics so you might want to have a look at those notes first
- You also need to know how to SKETCH graphs and use Number Lines
- REARRANGE so that your “quadratic >0” (or <0)
- FACTORISE the quadratic
- SKETCH a graph of the quadratic
- Use x-axis as a NUMBER LINE to show where the graph is above (if ≥ or >) or below (if ≤ or <) the x-axis
- Turn the number line into a PAIR of inequalities or a DOUBLE inequality
Exam Tip
- When dealing with quadratic inequalities always make sure that you end up with a positive number in front of the x2
- For example, to solve the inequality 4 - 2x2 > 5x start by adding the 2x2 to (and subtracting 4 from both sides to get 0 > 2x2 + 5x -4) rather than subtracting the 5x (and getting 4 - 5x -2x2 > 0)
- Why? Because it’s much easier to factorise a quadratic when the coefficient of x2 is positive
Worked Example
Worked Example
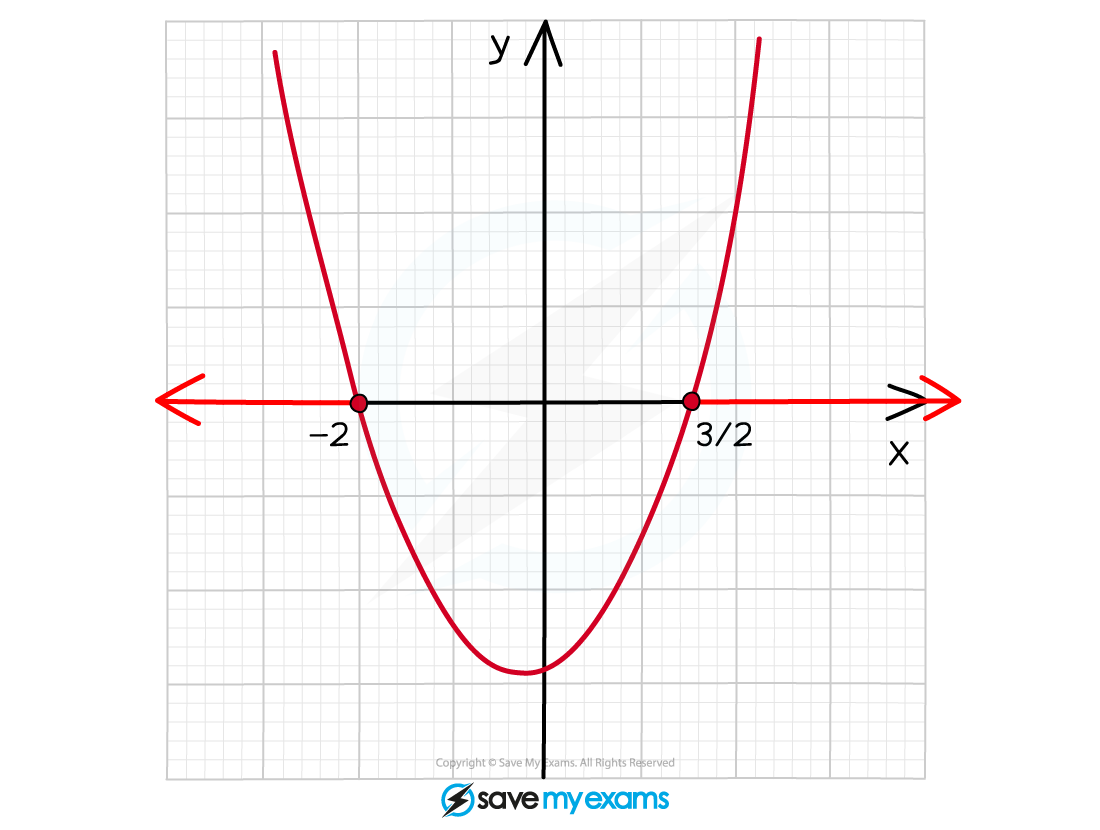
Worked Example
Worked Example
Worked Example
Worked Example
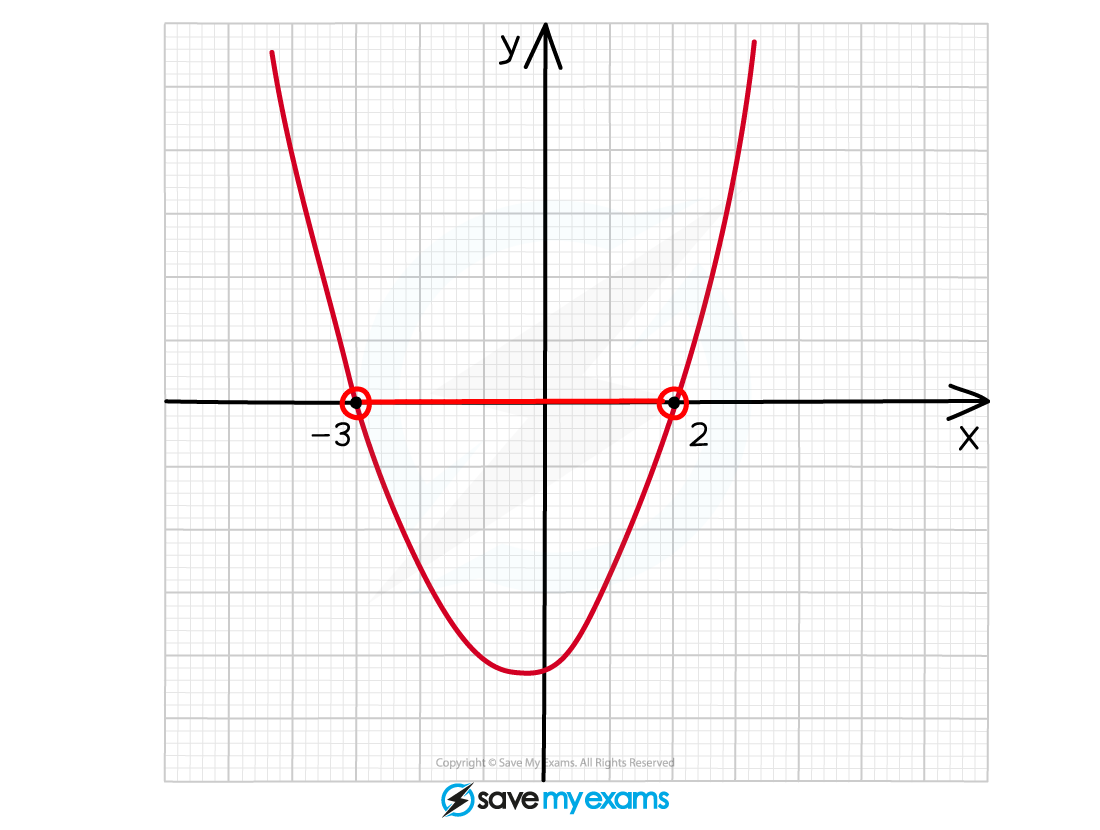
Worked Example
转载自savemyexam
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
