2022AIME美国数学竞赛邀请赛及历年真题下载
AIME由AMC10和AMC12的优胜者参加，参加标准为：AMC10全球前2.5%或AMC12全球前5%，具体晋级比例每年根据参赛人数的比赛结果会有所变化。
AIME是介于AMC10、AMC12及美国数学奥林匹克学术活动（USAMO）之间的一个数学学术活动，主要目的是结合AMC10和12的成绩筛选出晋级USAMO的选手，进而通过下一步的比赛与暑期集训（MOP）选拔出6位最终参加IMO（国际数学奥林匹克）的美国国家队成员。学术活动开始于1983年。2000年起AIME增加一场比赛，分为AIME I和AIME II两场。
2022AIME I 真题及答案
翰林学院整理了1983年来全部AIME真题及解答
（下载方式见文末）
AIME比赛时间在2021年之前为每年的3月中旬与三月底，2021年秋季改制之后，自2022年起为每年的2月中旬与下旬分别举行I卷与II卷的考试。
AIME的考题相对于AMC10及AMC12而言更具难度，给晋级的学生提供了更进一步的挑战和数学能力水平认证的可能。
AIME成绩优异的具有美国身份的学生将再被邀请参加USJMO和USAMO数学学术活动，对于非美国籍的学生，AIME就是AMC系列比赛选拔的终点，但在数学方面有优异才能的学生，也可以通过与其他参赛选手获得的成绩进行对比对自己的数学能力得到肯定。
考试形式
AIME学术活动考试时间为3小时，一共15道填空题，一题一分，满分15分，每题的得分只看最后答案是否正确而不需要提供解答的过程，比赛中不允许使用计算器。AIME问题的难度会随着题目编号的增加而逐渐加大，其前面大部分题目和AMC12最后十题的难度基本相当，最后三道题一般会均有相当的挑战性，甚至达到olympiad入门题目的水平。
考试安排
AIME目前在每年2月中旬与下旬举办。
考试内容
AIME 的考试内容基本与AMC12相当，但在数论、代数、几何、组合各个核心板块中有进一步的加深和拓展。比如数论部分主要引入了少量olympiad级别比赛涉及到的概念与结果，比如阶和原根的概念，中国剩余定理的熟练应用，Wilson定理、LTE升幂引理的应用。
代数部分显著增加了题目的运算量，包括复杂三角恒等式（和差化积，积化和差，三角形内的三角恒等式）的运用，高斯函数相关问题的考察，以及复数、向量等工具在数形结合问题中的应用。
几何部分同样显著增加了题目的运算量，三角工具、坐标工具、复数工具在几何题目解决过程中的重要性进一步增加，同时部分较难题目适当引入了入门级别olympiad题目的常见几何构型，对于晋级到下一轮MO的选手熟悉、学习相关专业内容起到一个承接的作用。组合部分的题目加大了对于递归方法的应用，复杂容斥原理的应用以及与其他板块交叉、具有复合背景的计数问题的考察。
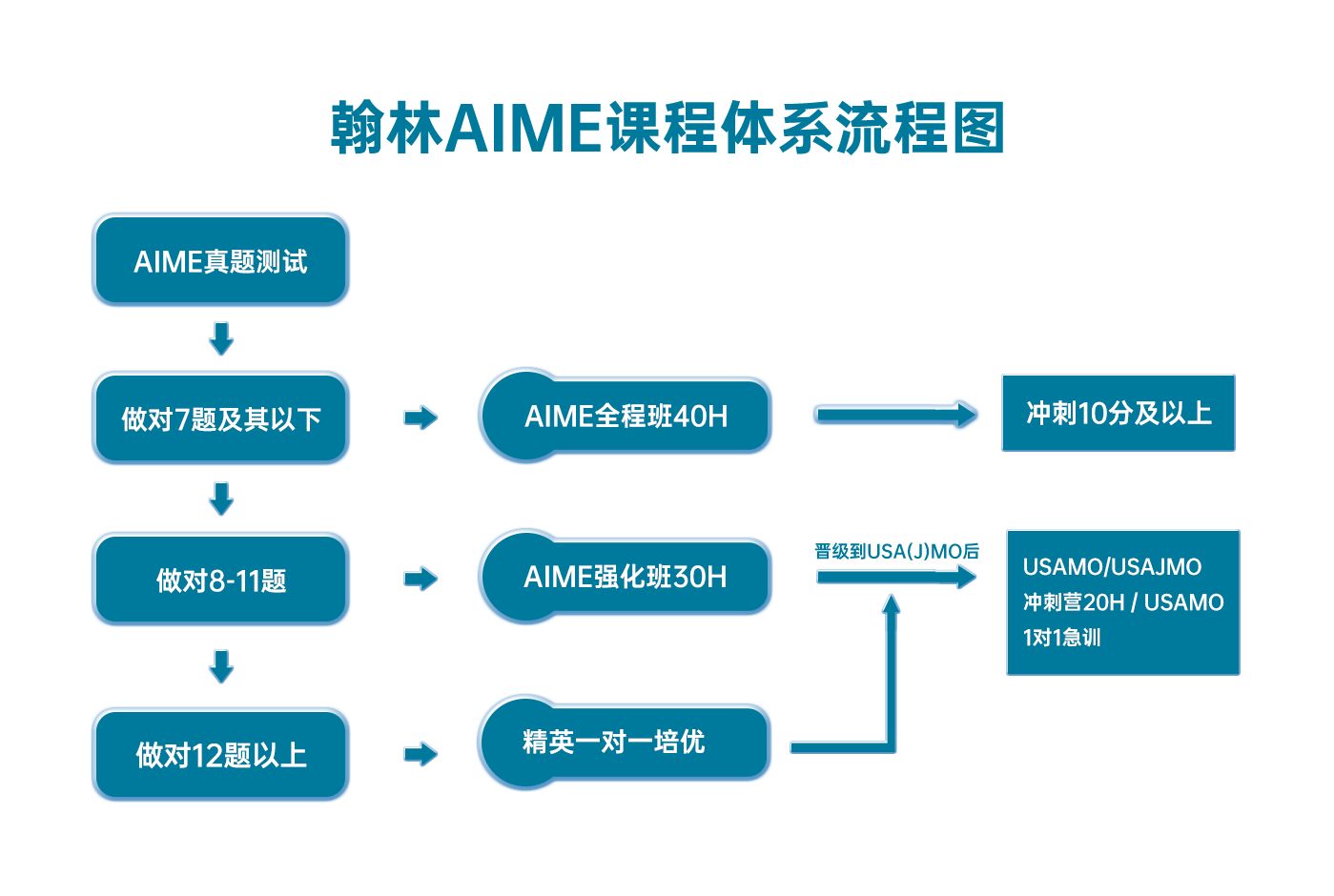
翰林AIME课程体系流程图
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
