学霸私藏AP统计5分必考点梳理，省时又高效！速度收藏
概述
统计按照大纲共分为四部分，分别是描述统计、抽样方法、概率论、统计推断。
(1) Exploring Data: Describing patterns anddepartures from patterns
(2) Sampling and Experimentation: Planningand conducting a study
(3) Anticipating Patterns: Exploring randomphenomena using probability and simulation
(4) Statistical Inference: Estimatingpopulation parameters and testing hypotheses
1描述统计
数据（data）分为定性数据（qualitative or categorical data）与定量数据（quantitativedate）。定性数据：按照类别进行划分，展示对象的属性；定量数据：展示对象的数值特征。
图（graph）：分为bar chart, pie chart, dotplot, stemplot, histogram, boxplot
| Quality | Quantity | |
| Bar chart | YES | NO |
| Pie chart | YES | NO |
| Stemplot | NO | YES |
| Dotplot | YES | YES |
| Histogram | NO | YES |
| Boxplot | NO | YES |
通过图形可以看出数据的分布特征
（1）对称（symmetric）
（2）偏态（skewed）左偏（skewed to the left）右偏（skewed to the right）
（3）集中趋势
（4）异常值
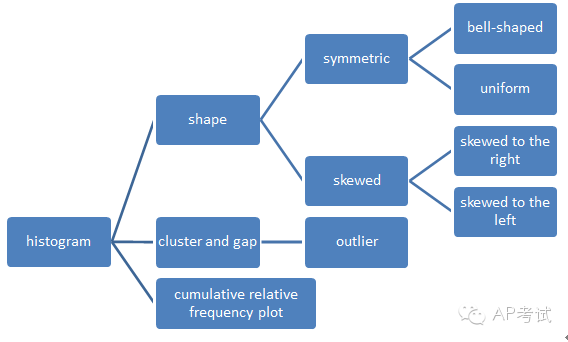
histogram的画法
（1）以个数作为高度（2）以百分比作为高度（3）以百分比作为面积。
概率密度（probability density function, pdf）
描绘以百分比作为面积的histogram的曲线。
累积分布（cumulative distribution function, cdf）
以小于等于该数的数据所占百分比作为该数的纵坐标绘制出的曲线。
数字特征（numerical value）
（1）描述集中趋势（2）描述离散趋势（3）描述位置（4）标准化变量（z-score）
| Center | Mode | Mean | Median | |
| Spread | Range | Interquartile range | Variance | Standard deviation |
| Position | Simple ranking | Percentile ranking | ||
| Z-score |
众数（mode）
一组数据中出现次数最多的数。
平均数（mean）
数据求和后除以数据个数。
数据的排序方式（从小到大）有两种
（1）简单排序（simple ranking）：第一、第二、第三等等（2）百分位排序（percentile ranking）：
某个数的百分位值等于小于该数的数据个数占整体的百分比。
将一组数据排序后，可得到
a.最小值（minimum）、最大值（maximum）
b.极差（range）：最大值与最小值的差，max-min
c.中位数（median）：排序后处于中间位置的数
d.四分位数（quartile）：
位于25%、75%的数，记为Q1、Q3
（1）.四分位差（interquartile range, IQR）：两个四分位数的差值，IQR=Q3-Q1
（2）.判断某个数是否为异常值（outlier），可用Q1-1.5IQR和Q3+1.5IQR作为标准进行衡量，如果该数超出这个范围则可认定为异常值。
（3）箱线图（boxplot）：
剔除异常值后取最小值、Q1、中位数、Q3、最大值这五个数，最小值最大值作为两个端点，Q1、中位数、Q3作为三条线画出的图形。将异常值以散点的形式标注在最小值左侧和最大值右侧。
方差（variance）与标准差（standard deviation）：衡量数据与平均值偏离程度平方和的平均值。
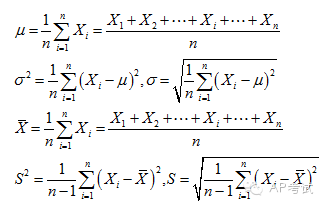
这里需要注意的是，如果计算的是总体的方差和标准差，用1/n来求平均；如果计算的是样本的方差和标准差，用1/(n-1)来求平均。
标准化变量（z-score）：计算方式是将原始数据减去平均数之后再除以标准差，用它可以展示不同度量单位数据的偏离程度。
二维数据二维定量数据研究两个变量的关系
以一个变量作为横坐标、另一个变量作为纵坐标绘制出的图形，以散点的形式表现在坐标轴中。变量选用单位不同，会造成图形有差异。
相关系数（linear correlation coefficient）
衡量两个量之间线性关系的指标，介于-1和1之间，负数代表两个变量之间是反向变化的，正数代表两个变量之间是同向变化的，越靠近0代表线性关系越弱，越靠近-1和1代表线性关系越强。它只能衡量线性关系，不能衡量非线性关系；只反应关系，不代表因果。
回归（regression）
寻找代表变量之间关系的数学表达式。
线性回归
假定变量之间存在一次函数的关系（形如y=kx+b）。此函数在坐标系中图像是一条直线，因此称作线性回归。
真实值与估计值之间的差。
残差图（residual plot）
以一个变量作为横坐标、该变量所对应的残差为纵坐标绘制出的图形。若两变量之间存在线性关系，则残差图应为无规则的散点。
最小二乘法（least square）
利用残差平方和最小求出直线斜率与截距（k和b）的方法。
线性化（linearity）
将非线性关系转换为线性关系的方法，常用有对数变换、指数变换等。
抽样方法
总体（population）：研究对象的全体。样本（sample）：
总体中的一部分。
参数（parameter）：
描述总体特征的指标，一般用希腊字母表示。
统计量（statistics）：
描述样本特征的指标，一般用拉丁字母表示。
普查（census）：
对总体中的每一个个体都进行研究。
抽样（sample）：
对总体中的部分个体进行研究。
实验法（experiment）：
对目标群体进行干预而得到数据。
观察法（observation）：
不对目标群体进行干预而得到数据。
实验组（treatment group）：
对该组中的个体进行干预。
对照组（control group）：
不对该组中的个体进行干预。
影响因子（factor）:
会对实验对象产生影响
变量混淆（confounded）：
无法分离因子的影响
协同作用（common response）：
多个因子共同造成影响
安慰剂（the placebo effect）：
心理作用导致的变化
单盲试验（single blinding）：
实验者知晓每一个体是否受到预先设置的干预，而被实验者不知晓。
双盲试验（double blinding）：
实验者与被实验者都不知晓每一个体是否受到预先设置的干预。
简单随机抽样（simple random sampling）：
随机地从总体中选取个体，每个个体被选到的概率是相等的。
系统抽样（systematic sampling）：
首先将总体中的个体编号、排序，而后按照固定步长进行抽样。
分层抽样（stratified sampling）：
首先将总体中的个体按照某一特征或标准划分为不同的层（strata），而后从每层中进行抽样。特征是每个层中的个体具有相似性。
整群抽样（cluster sampling）：
首先将不同特征的个体划为分一个群（cluster），而后从每个群中进行抽样。特征是每个群具有多样性。
概率
频数（frequency）：某一结果出现的次数。
频率（relative frequency）：
某一结果出现的次数占实验次数的百分比。
概率（probability）：
某一结果出现可能性的大小，介于0和1之间。不可能事件（impossible event）的概率是0，必然事件（certain event）的概率是1，但反之不正确，概率为0的事件不一定是不可能事件，也有可能发生，概率为1的事件也可能不发生。
大数定律（the law of large numbers）：
实验次数越大，频率越稳定，且取决于事件本身的概率。
基本公式：
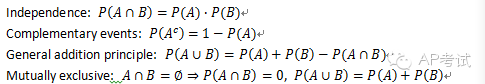
条件概率（conditional probability）：
给定某一事件发生的条件下，另一事件发生的概率。
随机变量（random variable）：
该变量的取值取决于实验的结果。
离散型（discrete）：
随机变量的取值是一个一个的。
连续型（continuous）：随机变量的取值是连续不间断的。
分布（distribution）：
实验结果出现的规律。
均值（mean）与方差（variance）:
二项分布（binomial distribution）：
将具有两个结果的实验重复多次，求其中某一结果出现次数的概率。
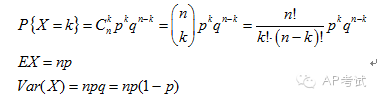
几何分布（geometric distribution）：
将具有两个结果的实验重复多次，求其中某一结果首次出现时实验次数的概率。
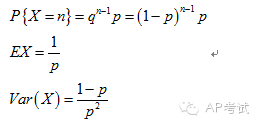
正态分布（normal distribution）：
代表常规现象出现次数多、极端现象出现次数少这样一种规律。
标准正态分布（standard normal distribution）：
均值为0、方差为1的正态分布。
抽样分布（sampling distribution）：
多次抽样后，样本统计量的分布规律。
标准误（standard error）：
统计量的标准差。
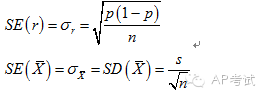
单总体样本比例的抽样分布
统计推断
参数估计（estimation）：利用统计量去预测参数。区间估计（interval）：
给出参数的范围。
置信水平（confidence level）：
对参数多次进行估计得到多个区间，其中区间中包含真实参数的次数占估计次数的比例。
单总体比例区间估计：
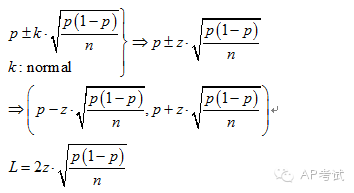
双总体比例差区间估计：
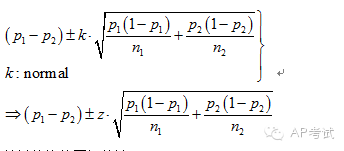
单总体均值区间估计：
此时需考虑总体方差是否已知，（1）若已知则使用正态分布进行估计，（2）若未知则使用t分布进行估计。
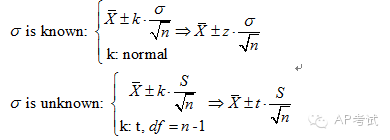
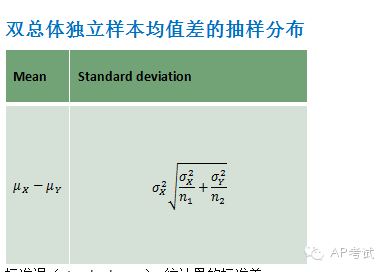
双总体均值差区间估计：
此时需考虑总体方差是否已知
（1）若已知则使用正态分布进行估计
（2）若未知
a.总体方差不等（pooled=no）
b.总体方差相等（pooled=yes），则使用t分布进行估计，但所用自由度与方差皆不相同。
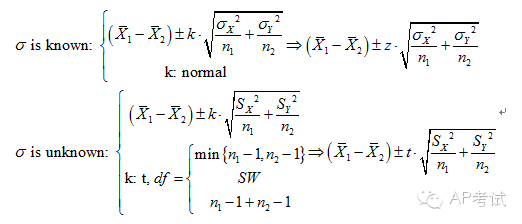
假设检验（hypothesis test）：
利用统计量对参数的真伪进行检验。
原假设（null hypothesis）：
待检验参数。
备择假设（alternative hypothesis）：
当原假设被拒时所接受的假设。
根据备择假设形式的不同，分为双尾检验（two tailed）和单尾检验（one tailed）
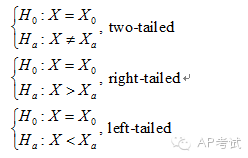
p值（p-value）：
当原假设为真的时候得到此样本结果以及比此样本结果更极端结果的概率。p值越小，拒绝原假设的可能性越大。
第一类错误（type I error）：原假设为真时却拒绝原假设。犯此错误的概率为显著性水平（significance level）。
第二类错误（type II error）：原假设为假时却没有拒绝原假设。不犯此类错误的概率成为检验的power（power of the test）。
在样本容量（sample size）固定的条件下，两类错误为此消彼长的关系，若想同时降低两类错误，只能提升样本容量。
单总体比例检验：
双总体独立样本比例差检验：
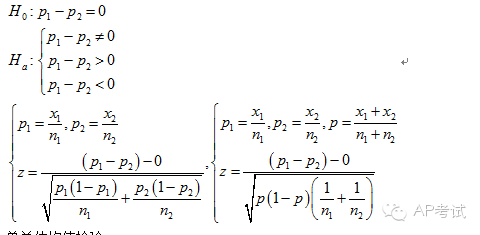
单总体均值检验：
此时需考虑总体方差是否已知
（1）若已知则使用正态分布进行检验
（2）若未知则使用t分布进行检验。
双总体均值差检验：
此时需考虑总体方差是否已知
（1）若已知则使用正态分布进行检验
（2）若未知
a.总体方差不等（pooled=no）
b.总体方差相等（pooled=yes），则使用t分布进行估计，但所用自由度与方差皆不相同。
卡方检验（Chi-square）
拟合优度检验（goodness of fit）：利用样本信息来检验总体是否符合某一分布。
独立性检验（independence）：检验某一分类结果是否受另一分类影响。
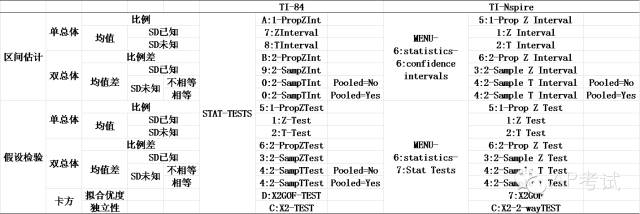
计算器命令列表
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
