2022AP物理C力学北美卷FRQ已放出，附考情分析

各位AP小伙伴们好呀~2022年5月10日进行的AP物理C力学考试已经结束，本场考试为线下纸笔考试，CB官网已更新了2022AP物理C力学北美FRQ真题。

2022年的AP物理C力学考试已经结束，今天官方放出了两个Set的FRQ，我们赶紧一起来看看都考了哪些内容吧！

试卷整体难度和知识点

两个Set的对应题目考的知识点相近，第1题主要是考察牛顿运动定律，第2题主要在考察动量和实验分析，第3题主要是考察转动的牛顿第二定律。整体的难度中等，有的题目和往年题目极为相似；此外，涉及实验分析和图像解释的题目可能略难，刚体转动的题目个别小题可能略难。整体相比2021年考试难度来看，难度系数有所下降。

与2021年题目对比的点评

第1道题比较新颖，之前没有出现过类似的变力分析问题，可以作为今年新出现的题目类型进行重点研究；第2道题目，相信大家都比较眼熟，第2道题目考察的题目模型和2021年很类似，都是一个物块沿斜面下滑，在右端有运动检测装置等，只不过第2道题目引入了动量和能量，并在此基础上进行考察；第3道题目的图像问题和2021年极为类似，考察的知识点和解题方法近乎吻合。

因此，大家如果做了2021年的北美题的话，相信大家这套题目一定可以拿到理想的分数。

逐题点评

第一题
Set1
一个电动机在左侧下方提供一个大小恒定不变的拉力，放在桌子上的小物体受到绳子拉力的作用往左滑动，小物体和桌面之间有摩擦力，均不考虑其余位置的摩擦力和其余物体的质量。
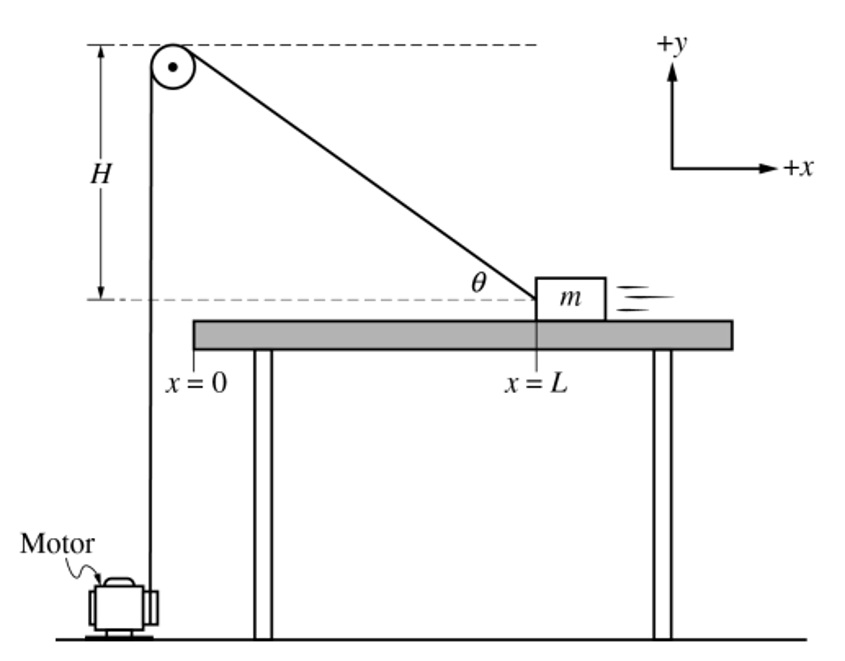（a）画出小物块在x=L位置处的受力分析图。
考点：Unit 2牛顿运动定律中的受力分析图。
思路：小物块受到向下的重力、向上的支持力、沿绳子斜向左上方的拉力和水平向右的摩擦力。在这里要特别注意摩擦力的方向，与物块的运动方向相反。

（b）推导绳子与水平面的夹角θ与水平位置x的函数关系。
考点：Unit 1位移和三角函数关系。
思路：从图中可以看出，位移x、竖直高度H、滑轮到物块的斜着的绳子的长度，构成一个直角三角形，利用正切函数关系，可以找到绳子与水平面的夹角θ与水平位置x的表达式。

（c）
i：推导物块受到的支持力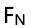和水平位置x的函数关系。
考点：Unit 2中的牛顿第一定律。
思路：根据竖直方向上受力平衡，可以写出，得出，然后再将sinθ按照三角形的边之间的关系进行替换就好。

ii：推导物体所受的合力与水平位置x的关系表达式。
考点：Unit 2中的牛顿第二定律。
思路：根据水平方向上物体受力不平衡、竖直方向上物体受力平衡可以推断出，物体受到的合力就是水平方向上的合力。根据受力分析图，写出水平方向的牛顿第二定律表达式： ;再将摩擦力利用进行替换带入可以得到合力的最终受力表达式，最后的话，再将三角函数表达式利用几何三角形的边进行替换就好。

（d）写出（但不用求解）从x=L到x=0绳子拉力做功的表达式。
考点：Unit 3中的变力做功问题。
思路：根据变力做功，直接写出变力做功积分式就好。

（e）比较绳子从x=L到x=L/2、从x=L/2到x=0做功的大小。
考点：Unit 3中的变力做功问题。
思路：从x=L到x=L/2、x=L/2到x=0拉力的水平位移都一样，因此判断拉力前后两段位移做功大小，只需要判断拉力的水平分力大小就好，拉力的水平分量表达式为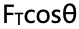，随着物块向左滑动，θ在增大，cosθ在减小，所以拉力的水平分力也在减小，所以平均来看，前半段拉力的水平分力大于后半段的水平分力，所以前半段拉力做功会更大一些。

扫码添加翰林顾问老师，可一对一制定国际课程规划
【免费领取】AP备考资料合集~

 Set2
一个质量为m的小雪橇在受到绳子的拉力和桌面摩擦力的条件下，给定一个初速度，向右进行滑动。其中绳子的拉力大小恒定不变，不考虑其余位置的摩擦和其余物体的质量。
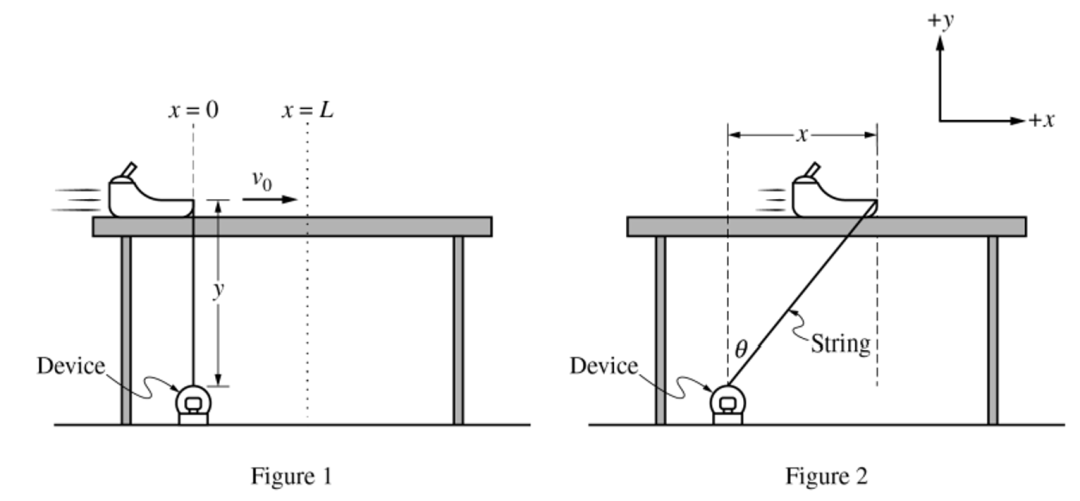（a）画出运动开始很小一段时间后（小雪橇停止运动前的某个时刻），小雪橇的受力分析图。
考点：Unit 2牛顿运动定律中的受力分析图。
思路：小雪橇受到向下的重力、向上的支持力、沿绳子斜向左下方的拉力和水平向左的摩擦力。在这里要特别注意摩擦力的方向，与小雪橇的运动方向相反。

（b）推导绳子与竖直方向的夹角θ与运动距离x的函数关系。
考点：Unit 1位移和三角函数关系。
思路：从图中可以看出，位移x、竖直高度y、左下方设备到小雪橇的斜着的绳子的长度，构成一个直角三角形，利用正切函数关系，可以找到绳子与竖直方向的夹角θ与运动距离x的表达式。

（c）
i：推导物块受到的支持力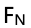和水平位置x的函数关系。
考点：Unit 2中的牛顿第一定律。
思路：根据竖直方向上受力平衡，可以写出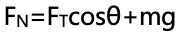，然后再将cosθ按照三角形的边之间的关系进行替换就好。

ii：推导物体所受的合力与水平位置x的关系表达式。
考点：Unit 2中的牛顿第二定律。
思路：根据水平方向上物体受力不平衡、竖直方向上物体受力平衡可以推断出，物体受到的合力就是水平方向上的合力，根据受力分析图，写出水平方向的牛顿第二定律表达式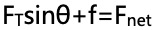：;再将摩擦力利用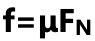进行替换带入可以得到合力的最终受力表达式，最后的话，再将三角函数表达式利用几何三角形的边进行替换就好。

（d）推导从x=0到x=L，绳子拉力做功的表达式。
考点：Unit 3中的变力做功问题。
思路：根据变力做功，写出变力做功积分表达式，再进行数学积分就好。这个题物理方程不难，但是数学积分难度会相应大一些，大家计算要仔细认真。

（e）小雪橇在运动水平距离2L后静止。比较系统从x=0到x=L、从x=L到x=2L由于摩擦力做功损耗掉的能量的大小。
考点：Unit 3中的非保守力做功和能量守恒。
思路：摩擦力做功的数值的绝对值就是系统损耗的能量。从x=0到x=L、从x=L到x=2L摩擦力的位移都一样，因此只需要比较这两段过程中摩擦力的大小，结合摩擦力的表达式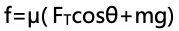，, θ在增大，cosθ在减小，摩擦力在减小，因此平均来看，前半段的摩擦力要比后半段的摩擦力要大，所以前半段摩擦力做功的绝对数值要大。

第二题
 Set1
小车1从斜面上往下滑，撞到静止在水平面上的小车2，然后二者共速在一起朝右运动。水平面的最右方有一个运动探测器，可以用来记录小车的运动。整个过程中不考虑摩擦和转动影响。
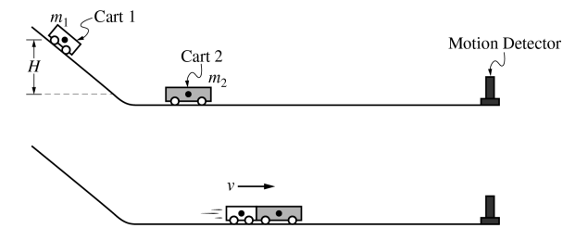（a）在碰撞过程中，比较小车1给小车2和小车2给小车1的冲量的大小关系。
考点：Unit 4中的冲量、Unit 2中的牛顿第三定律。
思路：根据牛顿第三定律，小车1给小车2的力和小车2给小车1的力等大反向，再结合二者作用力的时间相同，可以得出二者的冲量是相等的。

（b）画出碰撞前后，小车1和小车2的动量随时间变化的图像。
考点：Unit 4中的动量、动量定理和动量守恒定律。
思路：两小车碰撞前，小车1由静止开始下滑，速度均匀增加，到达平面后速度不变，因此小车1的动量先是直线型增加，再保持不变，小车2动量为0保持不变；碰撞后，因为系统动量守恒，小车2获得动量后保持不变，小车1的动量会减小一部分，然后继续保持不变；在这里要特别注意，小车1的动量减少量和小车2的动量增加量大小一样，建议在图像中把这层含义表示出来。

（c）题干给出了小车碰撞后的速度表达式，要我们进行证明。
考点：Unit 4中的动量守恒定律和Unit 3中的机械能守恒。
思路：利用机械能守恒，可以求得小车1运动到水平面（和小车2碰撞前）的速度；再根据动量守恒定律，可以求得系统碰撞后的速度表达式，即可得证。

（d）对于不同的释放高度H，测出系统共速后的速度v，给出了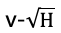的图像。要求画出最优拟合线并计算小车2的质量。
考点：最优拟合线的画法和通过直线斜率计算目标变量。
思路：根据上一问的速度表达式，最优拟合线应该是一条直线，注意画的时候不是连接所有点画折线而是要让不在直线上的数据大致平均分布在直线两侧，比如五个数据点可能有两个在直线上、一个在直线上方、两个在直线下方。这条直线的斜率是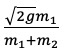，计算斜率的时候要注意不是取数据点而是取直线上的点，得到斜率之后通过计算便可得出小车2的质量。

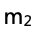（e）通过比较实验测得的数据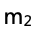和实际用天平测得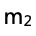的大小，来推断小车1质量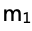与0.25 kg的大小关系。
考点：实验误差分析。
思路：可以根据斜率表达式，推导和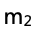的关系，从而再根据题干已知条件，再去反推小车1的质量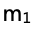和0.25 kg的大小关系。

 Set2
物块1在压缩弹簧一段距离的情况下，被弹簧推开（物块1与弹簧不连接）获得一个初速度，与水平面上静止的物块2发生完全非弹性碰撞，碰撞后一起共速向右运动。水平面右侧有运动探测器，用来记录系统的运动。不考虑各种摩擦。
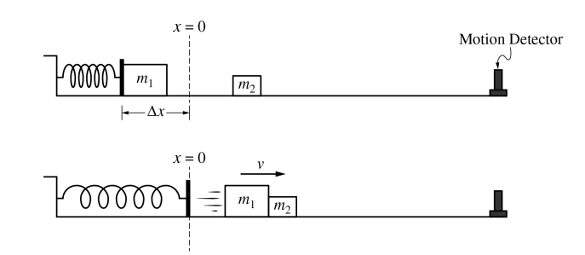（a）在碰撞过程中，比较物块1给物块2和物块2给物块1的冲量的大小关系。
考点：Unit 4中的冲量、Unit 2中的牛顿第三定律。
思路：根据牛顿第三定律，物块1给物块2的力和物块2给物块1的力等大反向，再结合二者作用力的时间相同，可以得出二者的冲量是相等的。

（b）画出碰撞前后，物块1和物块2的动量随时间变化的图像。
考点：Unit 4中的动量、动量定理和动量守恒定律。
思路：两小车碰撞前：物块1先是受到弹簧的弹力做变速运动（随着弹簧伸长，加速度越来越小），离开弹簧后，做匀速运动，因此物块1的动量先是曲线增加（上凸类型）再保持不变，物块2动量为0保持不变；
碰撞后：因为系统动量守恒，物块2获得动量后保持不变，物块1原来的动量减小一部分，然后继续保持不变；在这里要特别注意，物块1的动量减少量和物块2的动量增加量大小一样，建议在图像中把这层含义表示出来。

（c）题干给出了物块碰撞后的速度表达式，要我们进行证明。
考点：Unit 4中的动量守恒定律和Unit 3中的机械能守恒。
思路：利用机械能守恒，可以求得物块1运动到水平面（和物块2碰撞前）的速度；再根据动量守恒定律，可以求得系统碰撞后的速度表达式，即可得证。

（d）对于不同的弹簧压缩距离Δx，测出系统共速后的速度v，给出了v-Δx的图像。要求画出最优拟合线并计算物块2的质量。
考点：最优拟合线的画法和通过直线斜率计算目标变量。
思路：根据上一问的速度表达式，最优拟合线应该是一条直线，注意画的时候不是连接所有点画折线而是要让不在直线上的数据大致平均分布在直线两侧，比如五个数据点可能有两个在直线上、一个在直线上方、两个在直线下方。这条直线的斜率是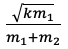，计算斜率的时候要注意不是取数据点而是取直线上的点，得到斜率之后通过计算便可得出物块2的质量。

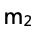（e）通过比较实验测得的数据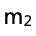和实际用天平测得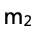的大小，来推断弹簧劲度系数k与150 N/m的大小关系。
考点：实验误差分析。
思路：可以根据斜率表达式，推导弹簧劲度系数k和物块2的质量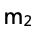的关系，从而再根据题干已知条件，再去反推弹簧劲度系数k与150 N/m的大小关系。

第三题
 Set1
一个有支柱的固体圆盘可以绕圆盘中心做无摩擦转动。一条绳子通过圆盘并且在圆盘的最顶端被固定住，记该点为P点。绳子的左下端连着一个弹簧，右端连着一个物块。开始弹簧处于原长，在此初始条件下，开始慢慢释放右端的物块，使其缓慢运动，最终达到平衡的状态，此时圆盘的最顶端转过的角度为θ。题干中给出了圆盘围绕其中心旋转的转动惯量表达式。
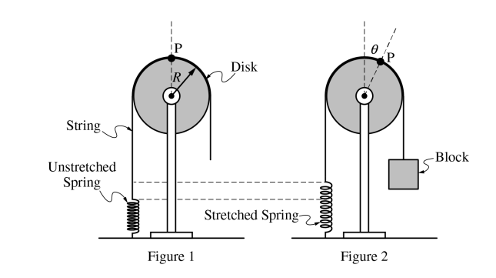（a）推导物块的质量表达式。
考点：Unit 2中的牛顿第一定律和胡克定律。
思路：物块受到绳子的拉力和自身重力，并且处于受力平衡；绳子的拉力又等于弹簧的拉力，因此，弹簧的拉力大小就是物块的重力大小；弹簧的拉力可以通过胡克定律F=kx求解，弹簧的形变量在这道题为圆盘转过的弧长，即θR。再利用弹簧的弹力除以g，即可求得物块的质量大小。

（b）在题干初始平衡的条件下，突然把连接物块的绳子剪断。画出剪断绳子的瞬间，圆盘的受力分析图。
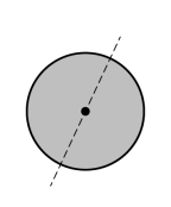考点：Unit 5中的受力分析图。
思路：剪断绳子的瞬间，圆盘受到质心发出向下的重力，质心方向向上的支持力和圆盘左端绳子和圆盘分离处沿切线方向向下的拉力。

（c）推导绳子剪断瞬间的系统角加速度的表达式。
考点：Unit 5中力矩的计算，转动形式的牛顿第二定律。
思路：圆盘受到三个力，但只有拉力是有力矩的，剪断绳子瞬间，拉力的大小为kθR，拉力的力臂为R，拉力的力矩为，再结合转动形式的牛顿第二定律，τ=Iα，可以得出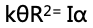，再代入圆盘的转动惯量，从而可以得出圆盘的角加速度。

（d）画出绳子剪断后，圆盘的角速度随时间变化的图像。时间截止到P点重新回到最高点的时刻。
考点：Unit 5中力矩的计算，转动形式的牛顿第二定律，角速率和角加速度的关系。
思路：根据（c）问，可以判断圆盘在P点重新回到最高点的过程中一直处于加速转动的状态，因此角速度在不断增大；而且，根据（c）中推出的角速度的表达式，可以看出角加速度随着θ的减小也会减小；因此，在转动过程中，θ在减小，所以角加速度也在减小，所以角速度-时间图像的斜率（斜率是角加速度）也在不断减小，因此，角速度-时间图像是上凸函数类型，且在P点重新回到最高点时，角速度达到最大，角加速度为0。

（e）转轴的支点位置改变后，圆盘受到的力的力矩和（b）问相比，是否发生变化，是变大还是变小。
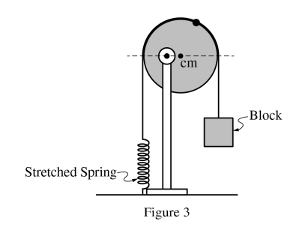考点：Unit 5中力矩的计算。
思路：支点改变后，圆盘受到的重力开始出现力矩，而（b）问没有，因此，重力力矩变大；拉力的力臂更加靠近转轴中心，力臂减小，所以拉力的力矩比（b）问中下降，因此，拉力力矩变小。支柱给的支持力依旧没有力矩，故保持不变。

Set2
一根均匀的质量为m长度为L的棒子，左端连着一根弹簧，距左端L/4的位置有一个支点。开始由于一个学生右端拖着棒子，弹簧处于原长状态；然后，同学的手缓慢放松，棒子右端缓慢下降，最终在棒子水平的时候，同学的手彻底撤去，系统此时也处于平衡状态。题干给出木棒围绕该质点的转动惯量为I。
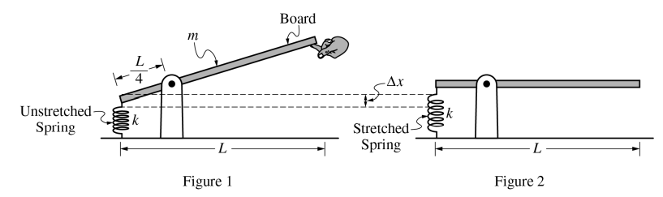（a）画出棒子水平位置平衡状态下的受力分析图。
考点：Unit 5中的受力分析图。
思路：棒子在最左端受到向下的弹簧的拉力，距离棒子左端L/4处，受到向上支点给的支持力；距离棒子左端L/2处，受到竖直向下的自身的重力。在转动的受力分析图里，物体受到的力不可以进行平移，要引起注意。

（b）推导木棒处于水平位置平衡状态时，弹簧的伸长量Δx的表达式。
考点：Unit 5中力矩的计算、转动形式的牛顿第一定律和胡克定律。
思路：木棒受到三个力，以支点为转动中心，只有弹簧的弹力和木棒自身的重力有力矩，且这两个力的力矩方向相反，大小相等。根据转动形式的牛顿第一定律，可以列出
kΔxL/4=mgL/4,从而可以计算得出Δx的表达式。
（c）另外一个学生在右端施加了一个新的力将木棒压至如下图所示位置，此时弹簧的伸长量为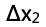，然后学生由静止释放木棒。（手施加的力突然撤掉）
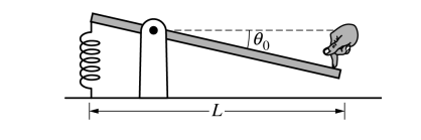i：画出木棒由静止开始转动至水平位置的过程中，角加速度随时间变化的表达式。
考点：Unit 5中力矩的计算，转动形式的牛顿第二定律，角加速度。
思路：木棒由静止释放后，木棒受到的弹簧的力矩大于自身重力的力矩，所以木棒受到的合力矩为τ= (kΔx-mg)Lcosθ/4，Δx为弹簧的伸长量, θ为木棒与水平位置的夹角；根据转动形式的牛顿第二定律，τ=Iα，可以得出， (kΔx-mg)Lcosθ/4= Iα；

随着时间的延伸，木棒受到的合力矩在减小，角加速度也在变小，但是角速度却在增加，因此位移变化的越来越快，力矩变化的速率也会变快，所以角加速度和时间图像的斜率会越来越陡；木棒处于水平位置时，木棒受到的合力矩为0，因此角加速度为0，所以角加速度是一个随着时间不断减小，并且在木棒回到水平位置的时刻减小到0的一个上凸函数类型。

ii：推导初始释放位置处，角加速度的表达式。
考点：Unit 5中力矩的计算，转动形式的牛顿第二定律，角加速度。
思路：木棒由静止释放后，木棒受到的弹簧的力矩大于自身重力的力矩，所以木棒受到的合力矩为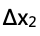，为弹簧的伸长量,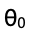为木棒与水平位置的夹角；根据转动形式的牛顿第二定律，τ=Iα，可以得出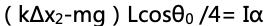，；经过进一步化简，便可得出角加速度的表达式。

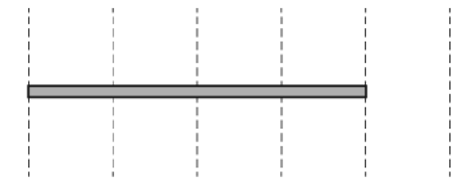
（d）如下图所示，在距离支点相同的位置处，固定两个质量为m的小物块，并在此前提下，木棒又被推至相同的位置处，并进行释放。问此时的角加速度和没有小物块时的角加速度的大小关系。
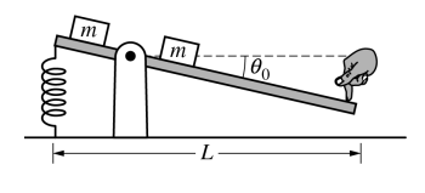考点：Unit 5中力矩的计算，转动形式的牛顿第二定律，角加速度、转动惯量。
思路：小物块添加后，系统的转动惯量会变大，但是系统的合外力矩却没有发生变化；因此，根据转动形式的牛顿第二定律，可以得出角加速度会下降。

写在最后
以上就是北美考情的分析了，对于备考明年考试的同学来说，应当注意对基础公式和模型的掌握，AP的出题风格并不会有太激进或太灵活的变化，和课内的呼应比较好，因此备考前重点研究往年考过的真题或者模考题也非常具有价值。