- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
【全网首发】2018AIME I卷真题及答案
2018 AIME I 真题
考试日期: 3月6日, 2018
答案解析请参考文末
Problem 1
Let ![]() be the number of ordered pairs of integers
be the number of ordered pairs of integers ![]() with
with ![]() and
and ![]() such that the polynomial
such that the polynomial ![]() can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when
can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when ![]() is divided by
is divided by ![]() .
.
Problem 2
The number ![]() can be written in base
can be written in base ![]() as
as ![]() , can be written in base
, can be written in base ![]() as
as ![]() , and can be written in base
, and can be written in base ![]() as
as ![]() , where
, where ![]() . Find the base-
. Find the base-![]() representation of
representation of ![]() .
.
Problem 3
Kathy has ![]() red cards and
red cards and ![]() green cards. She shuffles the
green cards. She shuffles the ![]() cards and lays out
cards and lays out ![]() of the cards in a row in a random order. She will be happy if and only if all the red cards laid out are adjacent and all the green cards laid out are adjacent. For example, card orders RRGGG, GGGGR, or RRRRR will make Kathy happy, but RRRGR will not. The probability that Kathy will be happy is
of the cards in a row in a random order. She will be happy if and only if all the red cards laid out are adjacent and all the green cards laid out are adjacent. For example, card orders RRGGG, GGGGR, or RRRRR will make Kathy happy, but RRRGR will not. The probability that Kathy will be happy is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
In ![]() and
and ![]() . Point
. Point ![]() lies strictly between
lies strictly between ![]() and
and ![]() on
on ![]() and point
and point ![]() lies strictly between
lies strictly between ![]() and
and ![]() on
on ![]() so that
so that ![]() . Then
. Then ![]() can be expressed in the form
can be expressed in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 5
For each ordered pair of real numbers ![]() satisfying
satisfying![]() there is a real number
there is a real number ![]() such that
such that![]() Find the product of all possible values of
Find the product of all possible values of ![]() .
.
Problem 6
Let ![]() be the number of complex numbers
be the number of complex numbers ![]() with the properties that
with the properties that ![]() and
and ![]() is a real number. Find the remainder when
is a real number. Find the remainder when ![]() is divided by
is divided by ![]() .
.
Problem 7
A right hexagonal prism has height ![]() . The bases are regular hexagons with side length
. The bases are regular hexagons with side length ![]() . Any
. Any ![]() of the
of the ![]() vertices determine a triangle. Find the number of these triangles that are isosceles (including equilateral triangles).
vertices determine a triangle. Find the number of these triangles that are isosceles (including equilateral triangles).
Problem 8
Let ![]() be an equiangular hexagon such that
be an equiangular hexagon such that ![]() , and
, and ![]() . Denote
. Denote ![]() the diameter of the largest circle that fits inside the hexagon. Find
the diameter of the largest circle that fits inside the hexagon. Find ![]() .
.
Problem 9
Find the number of four-element subsets of ![]() with the property that two distinct elements of a subset have a sum of
with the property that two distinct elements of a subset have a sum of ![]() , and two distinct elements of a subset have a sum of
, and two distinct elements of a subset have a sum of ![]() . For example,
. For example, ![]() and
and ![]() are two such subsets.
are two such subsets.
Problem 10
The wheel shown below consists of two circles and five spokes, with a label at each point where a spoke meets a circle. A bug walks along the wheel, starting at point ![]() . At every step of the process, the bug walks from one labeled point to an adjacent labeled point. Along the inner circle the bug only walks in a counterclockwise direction, and along the outer circle the bug only walks in a clockwise direction. For example, the bug could travel along the path
. At every step of the process, the bug walks from one labeled point to an adjacent labeled point. Along the inner circle the bug only walks in a counterclockwise direction, and along the outer circle the bug only walks in a clockwise direction. For example, the bug could travel along the path ![]() , which has
, which has ![]() steps. Let
steps. Let ![]() be the number of paths with
be the number of paths with ![]() steps that begin and end at point
steps that begin and end at point ![]() . Find the remainder when
. Find the remainder when ![]() is divided by
is divided by ![]() .
.
![[asy] size(6cm); draw(unitcircle); draw(scale(2) * unitcircle); for(int d = 90; d < 360 + 90; d += 72){ draw(2 * dir(d) -- dir(d)); } dot(1 * dir( 90), linewidth(5)); dot(1 * dir(162), linewidth(5)); dot(1 * dir(234), linewidth(5)); dot(1 * dir(306), linewidth(5)); dot(1 * dir(378), linewidth(5)); dot(2 * dir(378), linewidth(5)); dot(2 * dir(306), linewidth(5)); dot(2 * dir(234), linewidth(5)); dot(2 * dir(162), linewidth(5)); dot(2 * dir( 90), linewidth(5)); label("$A$", 1 * dir( 90), -dir( 90)); label("$B$", 1 * dir(162), -dir(162)); label("$C$", 1 * dir(234), -dir(234)); label("$D$", 1 * dir(306), -dir(306)); label("$E$", 1 * dir(378), -dir(378)); label("$F$", 2 * dir(378), dir(378)); label("$G$", 2 * dir(306), dir(306)); label("$H$", 2 * dir(234), dir(234)); label("$I$", 2 * dir(162), dir(162)); label("$J$", 2 * dir( 90), dir( 90)); [/asy]](http://latex.artofproblemsolving.com/4/f/6/4f679c03997360845c40254f779cfd4d8c33d3a1.png)
Problem 11
Find the least positive integer ![]() such that when
such that when ![]() is written in base
is written in base ![]() , its two right-most digits in base
, its two right-most digits in base ![]() are
are ![]() .
.
Problem 12
For every subset ![]() of
of ![]() , let
, let ![]() be the sum of the elements of
be the sum of the elements of ![]() , with
, with ![]() defined to be
defined to be ![]() . If
. If ![]() is chosen at random among all subsets of
is chosen at random among all subsets of ![]() , the probability that
, the probability that ![]() is divisible by
is divisible by ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 13
Let ![]() have side lengths
have side lengths ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() lies in the interior of
lies in the interior of ![]() , and points
, and points ![]() and
and ![]() are the incenters of
are the incenters of ![]() and
and ![]() , respectively. Find the minimum possible area of
, respectively. Find the minimum possible area of ![]() as
as ![]() varies along
varies along ![]() .
.
Problem 14
Let ![]() be a heptagon. A frog starts jumping at vertex
be a heptagon. A frog starts jumping at vertex ![]() . From any vertex of the heptagon except
. From any vertex of the heptagon except ![]() , the frog may jump to either of the two adjacent vertices. When it reaches vertex
, the frog may jump to either of the two adjacent vertices. When it reaches vertex ![]() , the frog stops and stays there. Find the number of distinct sequences of jumps of no more than
, the frog stops and stays there. Find the number of distinct sequences of jumps of no more than ![]() jumps that end at
jumps that end at ![]() .
.
Problem 15
David found four sticks of different lengths that can be used to form three non-congruent convex cyclic quadrilaterals, ![]() , which can each be inscribed in a circle with radius
, which can each be inscribed in a circle with radius ![]() . Let
. Let ![]() denote the measure of the acute angle made by the diagonals of quadrilateral
denote the measure of the acute angle made by the diagonals of quadrilateral ![]() , and define
, and define ![]() and
and ![]() similarly. Suppose that
similarly. Suppose that ![]() ,
, ![]() , and
, and ![]() . All three quadrilaterals have the same area
. All three quadrilaterals have the same area ![]() , which can be written in the form
, which can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
国际学术活动信息、辅导需求都可直接咨询,扫码免费领取学术活动真题及解析,助力高分!
2018 AIME I 详细解析请注册或登录后查看:
以上解析方式仅供参考
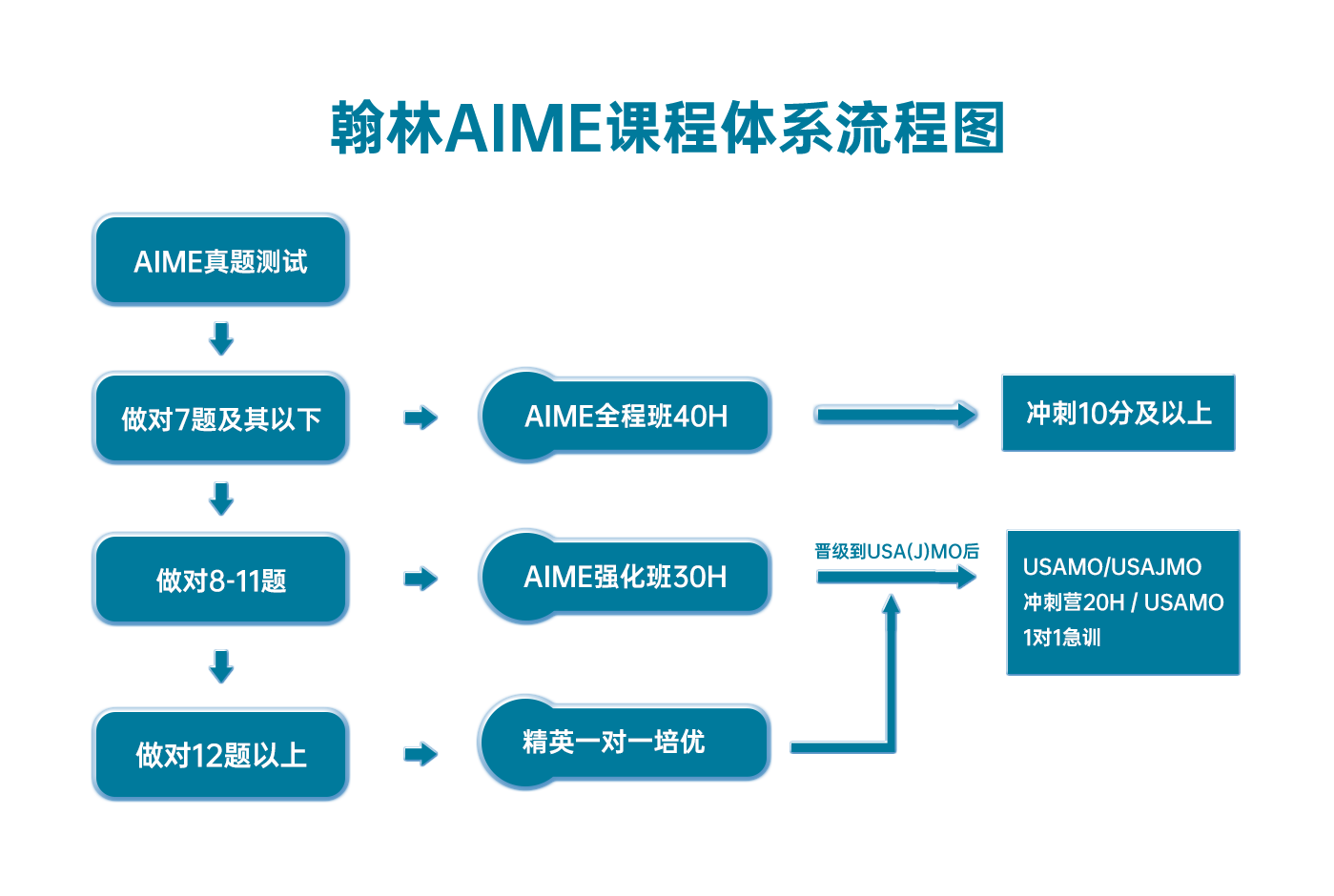
翰林AMC12课程体系流程图

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









