发刊词 | 用动图让你直观理解数学中的定理

图在数学中不算新的东西，不论在任何文化中，自从有了数字就有了图。

比如，表示1这个数字，可以画一条线表示，表示2这个数字，就画两条线。

当人们发现100，1000这样的数字用画一百一千根线很麻烦的时候，便发明了进制：用一种特殊的图，表示100，1000等等，这是图和代数的联系。 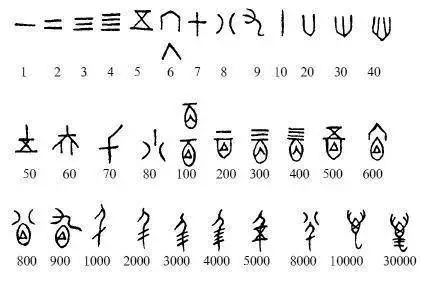图和几何的联系更多。

无论是中国的《周髀算经》还是外国的《几何原本》，在讲几何的时候必定会画图。

或者说，图就是一种数学语言，它在数学中的重要性丝毫不低于数字和字母，以至于平面几何、解析几何、立体几何贯穿整个中学数学。

说到中学数学教学，大家会想到中学时代老师在黑板上画着各种图形，写着各种公式。大家有没有遇到这种情况，老师说：“看，这条线长度恒过这一点”

“看，这个比值算出来一定是2”

大家脑子里却对这个“恒等于”“顶点”的问题没有一个直观的感觉，好像只是算出来的，不是看出来的。一、二十年前数学教学是这样可以理解，但2018年的今天，我们的数学基础教学在很多地方依然是这样讲这样学，很多学生觉得不好直观理解的东西依然不好理解。我就在想，我做什么

能帮助正在初中入门数学的学生直观的理解这些概念？答案就是：学数学到底是在研究什么？在我看来，是研究数字之间的连系和图形之中的变换。如果大家能能预先对于这个过程有个直观的印象，再去证明和记忆就不难了。现在数学教学中就缺乏一个直接能看到的过程。我来举个例子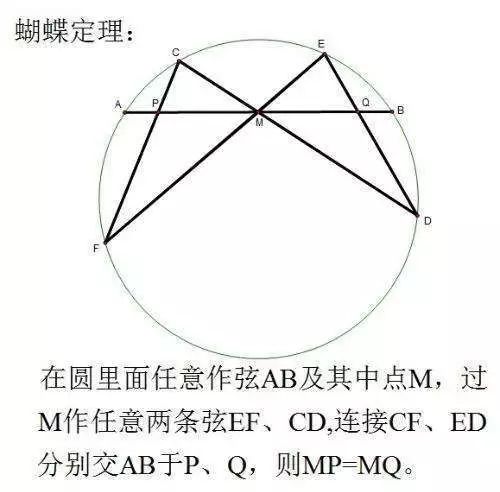：上图是传统的教学方法：这个定理首先有三步作图过程，做出线段MP和MQ后，大家对它的长度是不是一定相等的不确定，看到结论说的是相等，云里雾里地就着手去证明，忽略了一个更重要的事：让学生亲眼看到相等。

只有亲眼看到了无论图形怎样变化结论都是成立的，才能把这个知识直观的理解，而非死记硬背。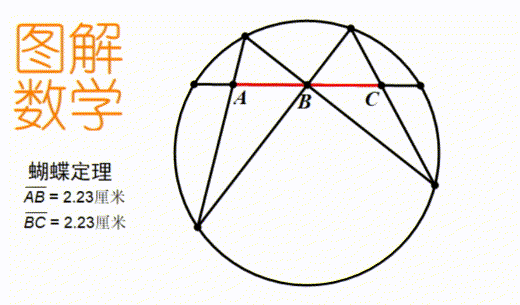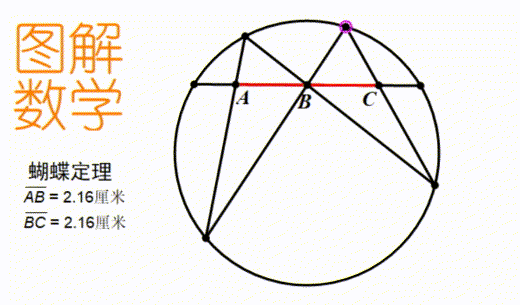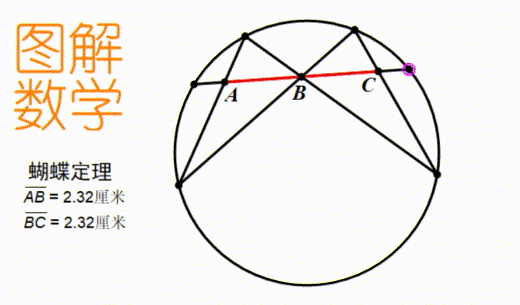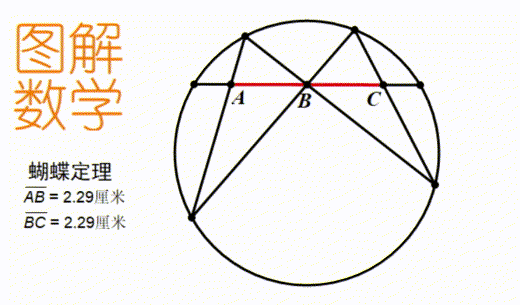动图是我提倡的数学学习新工具。它既不像视频那么麻烦，又不像定图那样只能反映一个时刻的信息。比如上图，我们可以直观地看到，无论这三条弦怎么变化，测量出的AB和BC的长度永远都一样。

这种变化中的不变性，正是数学里要研究的。所以，花几秒钟看这个动图，比对着定图

记忆十几分钟都有用。这也正是我所想的，2018年的数学教学应该比一二十年前进步的地方。

当然，证明过程也是不可替代的。

其他学科，比如物理化学，研究方法是：如果做实验出来结果符合理论，那么理论就是对的。

而数学的研究方法是：即使举出一千个一万个图形是对的，也不能充分地说明这个定理是对的。想说明一个定理的正确性，要靠严谨的证明。

《图解数学》系列每个定理都会告诉大家如何证明。