- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2022AIME II 真题及答案
2022AIME II 真题及答案
2022AIME I 真题及答案
Problem1
Adults made up ![]() of the crowd of people at a concert. After a bus carrying
of the crowd of people at a concert. After a bus carrying ![]() more people arrived, adults made up
more people arrived, adults made up ![]() of the people at the concert. Find the minimum number of adults who could have been at the concert after the bus arrived.
of the people at the concert. Find the minimum number of adults who could have been at the concert after the bus arrived.
Solution 1
Let ![]() be the number of people at the party before the bus arrives. We know that
be the number of people at the party before the bus arrives. We know that ![]() , as
, as ![]() of people at the party before the bus arrives are adults. Similarly, we know that
of people at the party before the bus arrives are adults. Similarly, we know that ![]() , as
, as ![]() of the people at the party are adults after the bus arrives.
of the people at the party are adults after the bus arrives. ![]() can be reduced to
can be reduced to ![]() , and since we are looking for the minimum amount of people,
, and since we are looking for the minimum amount of people, ![]() is
is ![]() . That means there are
. That means there are ![]() people at the party after the bus arrives, and thus there are
people at the party after the bus arrives, and thus there are ![]() adults at the party.
adults at the party.
~eamo
Solution 2 (Kind of lame)
Since at the beginning, adults make up ![]() of the concert, the amount of adults must be a multiple of 12.
of the concert, the amount of adults must be a multiple of 12.
Call the amount of people in the beginning ![]() .Then
.Then ![]() must be divisible by 12, in other words:
must be divisible by 12, in other words: ![]() must be a multiple of 12. Since after 50 more people arrived, adults make up
must be a multiple of 12. Since after 50 more people arrived, adults make up ![]() of the concert,
of the concert, ![]() is a multiple of 25. This means
is a multiple of 25. This means ![]() must be a multiple of 5.
must be a multiple of 5.
Notice that if a number is divisible by 5, it must end with a 0 or 5. Since 5 is impossible (obviously, since multiples of 12 end in 2, 4, 6, 8, 0,...), ![]() must end in 0.
must end in 0.
Notice that the multiples of 12 that end in 0 are: 60, 120, 180, etc.. By trying out, you can clearly see that ![]() is the minimum number of people at the concert.
is the minimum number of people at the concert.
So therefore, after 50 more people arrive, there are ![]() people at the concert, and the number of adults is
people at the concert, and the number of adults is ![]() . Therefore the answer is
. Therefore the answer is ![]() .
.
I know this solution is kind of lame, but this is still pretty straightforward. This solution is very similar to the first one, though.
~hastapasta
Problem2
Azar, Carl, Jon, and Sergey are the four players left in a singles tennis tournament. They are randomly assigned opponents in the semifinal matches, and the winners of those matches play each other in the final match to determine the winner of the tournament. When Azar plays Carl, Azar will win the match with probability ![]() . When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability
. When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability ![]() . Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is
. Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Let ![]() be Azar,
be Azar, ![]() be Carl,
be Carl, ![]() be Jon, and
be Jon, and ![]() be Sergey. The
be Sergey. The ![]() circles represent the
circles represent the ![]() players, and the arrow is from the winner to the loser with the winning probability as the label.
players, and the arrow is from the winner to the loser with the winning probability as the label.
This problem can be solved by using ![]() cases.
cases.
![]()
![]() 's opponent for the semifinal is
's opponent for the semifinal is ![]()
The probability ![]() 's opponent is
's opponent is ![]() is
is ![]() . Therefore the probability
. Therefore the probability ![]() wins the semifinal in this case is
wins the semifinal in this case is ![]() . The other semifinal game is played between
. The other semifinal game is played between ![]() and
and ![]() , it doesn't matter who wins because
, it doesn't matter who wins because ![]() has the same probability of winning either one. The probability of
has the same probability of winning either one. The probability of ![]() winning in the final is
winning in the final is ![]() , so the probability of
, so the probability of ![]() winning the tournament in case 1 is
winning the tournament in case 1 is ![]()
![]()
![]() 's opponent for the semifinal is
's opponent for the semifinal is ![]() or
or ![]()
It doesn't matter if ![]() 's opponent is
's opponent is ![]() or
or ![]() because
because ![]() has the same probability of winning either one. The probability
has the same probability of winning either one. The probability ![]() 's opponent is
's opponent is ![]() or
or ![]() is
is ![]() . Therefore the probability
. Therefore the probability ![]() wins the semifinal in this case is
wins the semifinal in this case is ![]() . The other semifinal game is played between
. The other semifinal game is played between ![]() and
and ![]() or
or ![]() . In this case it matters who wins in the other semifinal game because the probability of
. In this case it matters who wins in the other semifinal game because the probability of ![]() winning
winning ![]() and
and ![]() or
or ![]() is different.
is different.
![]()
![]() 's opponent for the final is
's opponent for the final is ![]()
For this to happen, ![]() must have won
must have won ![]() or
or ![]() in the semifinal, the probability is
in the semifinal, the probability is ![]() . Therefore, the probability that
. Therefore, the probability that ![]() won
won ![]() in the final is
in the final is ![]() .
.
![]()
![]() 's opponent for the final is
's opponent for the final is ![]() or
or ![]()
For this to happen, ![]() or
or ![]() must have won
must have won ![]() in the semifinal, the probability is
in the semifinal, the probability is ![]() . Therefore, the probability that
. Therefore, the probability that ![]() won
won ![]() or
or ![]() in the final is
in the final is ![]() .
.
In Case 2 the probability of ![]() winning the tournament is
winning the tournament is ![]()
Adding case 1 and case 2 together we get ![]() . So the answer is
. So the answer is ![]()
~isabelchen
Problem3
A right square pyramid with volume ![]() has a base with side length
has a base with side length ![]() The five vertices of the pyramid all lie on a sphere with radius
The five vertices of the pyramid all lie on a sphere with radius ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Although I can't draw the exact picture of this problem, but it is quite easy to imagine that four vertices of the base of this pyramid is on a circle (Radius ![]() ). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same:
). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same: ![]() . Because of the symmetrical property of the pyramid, we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.
. Because of the symmetrical property of the pyramid, we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.
Since the volume is ![]() , where
, where ![]() is the height of this pyramid, we have:
is the height of this pyramid, we have: ![]() according to pythagorean theorem.
according to pythagorean theorem.
Solve this equation will give us ![]() . Therefore,
. Therefore, ![]()
~DSAERF-CALMIT (https://binaryphi.site)
Solution 2
To start, we find the height of the pyramid. By the volume of a pyramid formula, we have![]() Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is
Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is ![]() , we have
, we have![\[x=\sqrt{\left(\frac92\right)^2+(3\sqrt2)^2}=\sqrt{\frac{153}4}=\frac{3\sqrt{17}}2.\]](https://latex.artofproblemsolving.com/7/5/6/7568a8673657eb8699e69661e8c82e765d9b2933.png) Taking the cross section of the pyramid and transforming the problem into
Taking the cross section of the pyramid and transforming the problem into ![]() -d, it suffices to find the radius of the circumcircle of a triangle of side lengths
-d, it suffices to find the radius of the circumcircle of a triangle of side lengths ![]() ,
, ![]() ,
, ![]() . This turns out to be easy by the formula
. This turns out to be easy by the formula ![]() , and through computing this value (the work has been left out) we find that
, and through computing this value (the work has been left out) we find that ![]() , so our answer is
, so our answer is ![]() .
.
~A1001
Problem4
There is a positive real number ![]() not equal to either
not equal to either ![]() or
or ![]() such that
such that![]() The value
The value ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Define ![]() to be
to be ![]() , what we are looking for. Then, by the definition of logs,
, what we are looking for. Then, by the definition of logs,![\[\begin{cases} (20x)^{a} &= 22x \\ (2x)^{a} &= 202x. \end{cases}\]](https://latex.artofproblemsolving.com/b/b/5/bb53f40f70a821a1ce25f078915aabb87e1b1d37.png) Dividing the first equation by the second equation gives us
Dividing the first equation by the second equation gives us ![]() , so by the definition of logs,
, so by the definition of logs, ![]() . This is what the problem asked for, so the fraction
. This is what the problem asked for, so the fraction ![]() gives us
gives us ![]() .
.
~ihatemath123
Solution 2
We could assume a variable ![]() which equals to both
which equals to both ![]() and
and ![]() .
.
So that ![]() and
and ![]()
Express ![]() as:
as: ![]()
Substitute ![]() to
to ![]() :
: ![]()
Thus, ![]() , where
, where ![]() and
and ![]() .
.
Therefore, ![]() .
.
~DSAERF-CALMIT (https://binaryphi.site)
Solution 3
We have
We have
Because ![]() , we get
, we get![]()
We denote this common value as ![]() .
.
By solving the equality ![]() , we get
, we get ![]() .
.
By solving the equality ![]() , we get
, we get ![]() .
.
By equating these two equations, we get![]()
Therefore,
Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Solution 4
By the change of base rule, we have ![]() , or
, or ![]() . We also know that if
. We also know that if ![]() , then this also equals
, then this also equals ![]() . We use this identity and find that
. We use this identity and find that ![]() . The requested sum is
. The requested sum is ![]()
~MathIsFun286
Problem5
Twenty distinct points are marked on a circle and labeled ![]() through
through ![]() in clockwise order. A line segment is drawn between every pair of points whose labels differ by a prime number. Find the number of triangles formed whose vertices are among the original
in clockwise order. A line segment is drawn between every pair of points whose labels differ by a prime number. Find the number of triangles formed whose vertices are among the original ![]() points.
points.
Solution 1
Let ![]() ,
, ![]() , and
, and ![]() be the vertex of a triangle that satisfies this problem, where
be the vertex of a triangle that satisfies this problem, where ![]() .
.![]()
![]()
![]()
![]() . Because
. Because ![]() is the sum of two primes,
is the sum of two primes, ![]() and
and ![]() ,
, ![]() or
or ![]() must be
must be ![]() . Let
. Let ![]() , then
, then ![]() . There are only
. There are only ![]() primes less than
primes less than ![]() :
: ![]() . Only
. Only ![]() plus
plus ![]() equals another prime.
equals another prime. ![]() .
.
Once ![]() is determined,
is determined, ![]() and
and ![]() . There are
. There are ![]() values of
values of ![]() where
where ![]() , and
, and ![]() values of
values of ![]() . Therefore the answer is
. Therefore the answer is ![]()
Problem6
Let ![]() be real numbers such that
be real numbers such that ![]() and
and ![]() . Among all such
. Among all such ![]() -tuples of numbers, the greatest value that
-tuples of numbers, the greatest value that ![]() can achieve is
can achieve is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
To find the greatest value of ![]() ,
, ![]() must be as large as possible, and
must be as large as possible, and ![]() must be as small as possible. If
must be as small as possible. If ![]() is as large as possible,
is as large as possible, ![]() . If
. If ![]() is as small as possible,
is as small as possible, ![]() . The other numbers between
. The other numbers between ![]() and
and ![]() equal to
equal to ![]() . Let
. Let ![]() ,
, ![]() . Substituting
. Substituting ![]() and
and ![]() into
into ![]() and
and ![]() we get:
we get:![]()
![]()
![]() ,
, ![]()
![]() .
. ![]()
~isabelchen
Solution 2
Define ![]() to be the sum of all the negatives, and
to be the sum of all the negatives, and ![]() to be the sum of all the positives.
to be the sum of all the positives.
Since the sum of the absolute values of all the numbers is ![]() ,
, ![]() .
.
Since the sum of all the numbers is ![]() ,
, ![]() .
.
Therefore, ![]() , so
, so ![]() and
and ![]() since
since ![]() is negative and
is negative and ![]() is positive.
is positive.
To maximize ![]() , we need to make
, we need to make ![]() as small of a negative as possible, and
as small of a negative as possible, and ![]() as large of a positive as possible.
as large of a positive as possible.
Note that ![]() is greater than or equal to
is greater than or equal to ![]() because the numbers are in increasing order.
because the numbers are in increasing order.
Similarly, ![]() is less than or equal to
is less than or equal to ![]() .
.
So we now know that ![]() is the best we can do for
is the best we can do for ![]() , and
, and ![]() is the least we can do for
is the least we can do for ![]() .
.
Finally, the maximum value of ![]() , so the answer is
, so the answer is ![]() .
.
(Indeed, we can easily show that ![]() ,
, ![]() , and
, and ![]() works.)
works.)
~inventivedant
Problem7
A circle with radius ![]() is externally tangent to a circle with radius
is externally tangent to a circle with radius ![]() . Find the area of the triangular region bounded by the three common tangent lines of these two circles.
. Find the area of the triangular region bounded by the three common tangent lines of these two circles.
Solution 1
![[asy] //Created by isabelchen size(12cm, 12cm); draw(circle((0,0),24)); draw(circle((30,0),6)); draw((72/5, 96/5) -- (40,0)); draw((72/5, -96/5) -- (40,0)); draw((24, 12) -- (24, -12)); draw((0, 0) -- (40, 0)); draw((72/5, 96/5) -- (0,0)); draw((168/5, 24/5) -- (30,0)); draw((54/5, 72/5) -- (30,0)); dot((72/5, 96/5)); label("$A$",(72/5, 96/5),NE); dot((168/5, 24/5)); label("$B$",(168/5, 24/5),NE); dot((24,0)); label("$C$",(24,0),NW); dot((40, 0)); label("$D$",(40, 0),NE); dot((24, 12)); label("$E$",(24, 12),NE); dot((24, -12)); label("$F$",(24, -12),SE); dot((54/5, 72/5)); label("$G$",(54/5, 72/5),NW); dot((0, 0)); label("$O_1$",(0, 0),S); dot((30, 0)); label("$O_2$",(30, 0),S); [/asy]](https://latex.artofproblemsolving.com/9/9/7/9975c6ddaea7f146407beccec628bc9733c584f7.png)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]()
![]()
~isabelchen
Solution 2
Let the center of the circle with radius ![]() be labeled
be labeled ![]() and the center of the circle with radius
and the center of the circle with radius ![]() be labeled
be labeled ![]() . Drop perpendiculars on the same side of line
. Drop perpendiculars on the same side of line ![]() from
from ![]() and
and ![]() to each of the tangents at points
to each of the tangents at points ![]() and
and ![]() , respectively. Then, let line
, respectively. Then, let line ![]() intersect the two diagonal tangents at point
intersect the two diagonal tangents at point ![]() . Since
. Since ![]() , we have
, we have![]() Next, throw everything on a coordinate plane with
Next, throw everything on a coordinate plane with ![]() and
and ![]() . Then,
. Then, ![]() , and if
, and if ![]() , we have
, we have![]()
![]() Combining these and solving, we get
Combining these and solving, we get ![]() . Notice now that
. Notice now that ![]() ,
, ![]() , and the intersections of the lines
, and the intersections of the lines ![]() (the vertical tangent) with the tangent containing these points are collinear, and thus every slope between a pair of points will have the same slope, which in this case is
(the vertical tangent) with the tangent containing these points are collinear, and thus every slope between a pair of points will have the same slope, which in this case is ![]() . Thus, the other two vertices of the desired triangle are
. Thus, the other two vertices of the desired triangle are ![]() and
and ![]() . By the Shoelace Formula, the area of a triangle with coordinates
. By the Shoelace Formula, the area of a triangle with coordinates ![]() ,
, ![]() , and
, and ![]() is
is![]()
Problem8
Find the number of positive integers ![]() whose value can be uniquely determined when the values of
whose value can be uniquely determined when the values of ![]() ,
, ![]() , and
, and ![]() are given, where
are given, where ![]() denotes the greatest integer less than or equal to the real number
denotes the greatest integer less than or equal to the real number ![]() .
.
Solution 1
We need to find all numbers between ![]() and
and ![]() inclusive that are multiples of
inclusive that are multiples of ![]() ,
, ![]() , and/or
, and/or ![]() which are also multiples of
which are also multiples of ![]() ,
, ![]() , and/or
, and/or ![]() when
when ![]() is added to them.
is added to them.
We begin by noting that the LCM of ![]() ,
, ![]() , and
, and ![]() is
is ![]() . We can therefore simplify the problem by finding all such numbers described above between
. We can therefore simplify the problem by finding all such numbers described above between ![]() and
and ![]() and multiplying the quantity of such numbers by
and multiplying the quantity of such numbers by ![]() (
(![]() /
/![]() =
= ![]() ).
).
After making a simple list of the numbers between ![]() and
and ![]() and going through it, we see that the numbers meeting this condition are
and going through it, we see that the numbers meeting this condition are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . This gives us
. This gives us ![]() numbers.
numbers. ![]() *
* ![]() =
= ![]() .
.
Soon after the test was administered, a formal request was made to also accept ![]() as an answer and MAA decided to honor this request. The gist of this request stated that the phrasing of the first part of the question could reasonably be interpreted to mean that one is given the condition to begin with that the integer is less than or equal to
as an answer and MAA decided to honor this request. The gist of this request stated that the phrasing of the first part of the question could reasonably be interpreted to mean that one is given the condition to begin with that the integer is less than or equal to ![]() . In this case, if one was told that the values of
. In this case, if one was told that the values of ![]() ,
, ![]() , and
, and ![]() were
were ![]() ,
, ![]() , and
, and ![]() respectively, then the only possible choice for
respectively, then the only possible choice for ![]() would be
would be ![]() as
as ![]() ,
, ![]() , and
, and ![]() do not meet the condition as stated in the first part of the problem. ~burkinafaso
do not meet the condition as stated in the first part of the problem. ~burkinafaso
Solution 1.5
This is Solution 1 with a slick element included. Solution 1 uses the concept that ![]() is a solution for
is a solution for ![]() if
if ![]() is a multiple of
is a multiple of ![]() ,
, ![]() , and/or
, and/or ![]() and
and ![]() is a multiple of
is a multiple of ![]() ,
, ![]() , and/or
, and/or ![]() for positive integer values of
for positive integer values of ![]() and essentially any integer value of
and essentially any integer value of ![]() . But keeping the same conditions in mind for
. But keeping the same conditions in mind for ![]() and
and ![]() , we can also say that if
, we can also say that if ![]() is a solution, then
is a solution, then ![]() is a solution! Therefore, one doesn't have to go as far as determining the number of values between
is a solution! Therefore, one doesn't have to go as far as determining the number of values between ![]() and
and ![]() and then multiplying by
and then multiplying by ![]() . One only has to determine the number of values between
. One only has to determine the number of values between ![]() and
and ![]() and then multiply by
and then multiply by ![]() . The values of
. The values of ![]() that work between
that work between ![]() and
and ![]() are
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . This gives us
. This gives us ![]() numbers.
numbers. ![]() *
* ![]() =
= ![]() .
.
Soon after the test was administered, a formal request was made to also accept ![]() as an answer and MAA decided to honor this request. The gist of this request stated that the phrasing of the first part of the question could reasonably be interpreted to mean that one is given the condition to begin with that the integer is less than or equal to
as an answer and MAA decided to honor this request. The gist of this request stated that the phrasing of the first part of the question could reasonably be interpreted to mean that one is given the condition to begin with that the integer is less than or equal to ![]() . In this case, if one was told that the values of
. In this case, if one was told that the values of ![]() ,
, ![]() , and
, and ![]() were
were ![]() ,
, ![]() , and
, and ![]() respectively, then the only possible choice for
respectively, then the only possible choice for ![]() would be
would be ![]() as
as ![]() ,
, ![]() , and
, and ![]() do not meet the condition as stated in the first part of the problem. ~burkinafaso
do not meet the condition as stated in the first part of the problem. ~burkinafaso
Solution 2
1. For ![]() to be uniquely determined,
to be uniquely determined, ![]() AND
AND ![]() both need to be a multiple of
both need to be a multiple of ![]() or
or ![]() Since either
Since either ![]() or
or ![]() is odd, we know that either
is odd, we know that either ![]() or
or ![]() has to be a multiple of
has to be a multiple of ![]() We can state the following cases:
We can state the following cases:
1. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
2. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
3. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
4. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
Solving for each case, we see that there are ![]() possibilities for cases 1 and 3 each, and
possibilities for cases 1 and 3 each, and ![]() possibilities for cases 2 and 4 each. However, we over-counted the cases where
possibilities for cases 2 and 4 each. However, we over-counted the cases where
1. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
2. ![]() is a multiple of
is a multiple of ![]() and
and ![]() is a multiple of
is a multiple of ![]()
Each case has ![]() possibilities.
possibilities.
Adding all the cases and correcting for over-counting, we get ![]()
~Lucasfunnyface
Solution 2 Supplement
Here is a detailed solution for Solution 2.

,

,
,
,
,
,
,
,
,
, 30 integers.

,

,
,
,
,
,
,
,
,
, 20 integers.

,

,
,
,
,
,
,
,
,
, 30 integers.

,

,
,
,
,
,
,
,
,
, 20 integers.
Over-counted cases:

,

,
,
,
,
,
,
,
,
,
,
, 10 integers.

,

,
,
,
,
,
,
,
,
,
,
, 10 integers.
![]()
~isabelchen
Solution 3
The problem is the same as asking how many unique sets of values of ![]() ,
, ![]() , and
, and ![]() can be produced by one and only one value of
can be produced by one and only one value of ![]() for positive integers
for positive integers ![]() less than or equal to 600.
less than or equal to 600.
Seeing that we are dealing with the unique values of the floor function, we ought to examine when it is about to change values, for instance, when ![]() is close to a multiple of 4 in
is close to a multiple of 4 in ![]() .
.
For a particular value of ![]() , let
, let ![]() ,
, ![]() , and
, and ![]() be the original values of
be the original values of ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
Notice when ![]()
![]() and
and ![]()
![]() , the value of
, the value of ![]() will be 1 less than the original
will be 1 less than the original ![]() . The value of
. The value of ![]() will be 1 greater than the original value of
will be 1 greater than the original value of ![]() .
.
More importantly, this means that no other value less than or greater than ![]() will be able to produce the set of original values of
will be able to produce the set of original values of ![]() ,
, ![]() , and
, and ![]() , since they make either
, since they make either ![]() or
or ![]() differ by at least 1.
differ by at least 1.
Generalizing, we find that ![]() must satisfy:
must satisfy:
Where ![]() and
and ![]() are pairs of distinct values of 4, 5, and 6.
are pairs of distinct values of 4, 5, and 6.
Plugging in the values of ![]() and
and ![]() , finding the solutions to the 6 systems of linear congruences, and correcting for the repeated values, we find that there are
, finding the solutions to the 6 systems of linear congruences, and correcting for the repeated values, we find that there are ![]() solutions of
solutions of ![]() .
.
Solution 3 Supplement
By Chinese Remainder Theorem, the general solution of systems of ![]() linear congruences is:
linear congruences is:
,
,
Find
and
such that
,
Then

![]() , we solve the number of values for
, we solve the number of values for ![]() , then multiply by
, then multiply by ![]() to get the number of values for
to get the number of values for ![]() . We are going to solve the following
. We are going to solve the following ![]() systems of linear congruences:
systems of linear congruences:

,

No solution

,


,

No solution

,

![]() , there are
, there are ![]() values for
values for ![]() . For
. For ![]() , the answer is
, the answer is ![]() .
.
~isabelchen
Sidenote
For solving a system of linear congruences, see https://youtu.be/-a88u99nmkw
Solution 4
Observe that if ![]() such that n is a solution to the desired equation, so is
such that n is a solution to the desired equation, so is ![]() , where m is an integer,
, where m is an integer, ![]() . So we only need to consider n from 1 to 60. As shown in Solution 2, there are 4 cases which we will split into 2 main cases:
. So we only need to consider n from 1 to 60. As shown in Solution 2, there are 4 cases which we will split into 2 main cases:
- Case 1:
 or
or  ,
, 
- Case 2:
 or
or  ,
, 
There are 4 values of n where ![]() satisfying
satisfying ![]() or
or ![]() .
.
I claim that there are 4 values of ![]() satisfying Case 1. Suppose x is one value of n satisfying
satisfying Case 1. Suppose x is one value of n satisfying ![]() or
or ![]() , and
, and ![]() . Hence the solutions satisfying
. Hence the solutions satisfying ![]() or
or ![]() ,
, ![]() are of the form
are of the form ![]() , so the values of
, so the values of ![]() are
are ![]() (mod 5), so
(mod 5), so ![]() (mod 5) and hence the value of m is unique since
(mod 5) and hence the value of m is unique since ![]() to satisfy
to satisfy ![]() and 2 and 5 are relatively prime.
and 2 and 5 are relatively prime.
A similar approach can be used to show the same for Case 2, that there are 4 values of ![]() .
.
Hence our answer is ![]() .
.
~Bxiao31415
Problem9
Let ![]() and
and ![]() be two distinct parallel lines. For positive integers
be two distinct parallel lines. For positive integers ![]() and
and ![]() , distinct points
, distinct points ![]() lie on
lie on ![]() , and distinct points
, and distinct points ![]() lie on
lie on ![]() . Additionally, when segments
. Additionally, when segments ![]() are drawn for all
are drawn for all ![]() and
and ![]() , no point strictly between
, no point strictly between ![]() and
and ![]() lies on more than two of the segments. Find the number of bounded regions into which this figure divides the plane when
lies on more than two of the segments. Find the number of bounded regions into which this figure divides the plane when ![]() and
and ![]() . The figure shows that there are 8 regions when
. The figure shows that there are 8 regions when ![]() and
and ![]() .
.![[asy] import geometry; size(10cm); draw((-2,0)--(13,0)); draw((0,4)--(10,4)); label("$\ell_A$",(-2,0),W); label("$\ell_B$",(0,4),W); point A1=(0,0),A2=(5,0),A3=(11,0),B1=(2,4),B2=(8,4),I1=extension(B1,A2,A1,B2),I2=extension(B1,A3,A1,B2),I3=extension(B1,A3,A2,B2); draw(B1--A1--B2); draw(B1--A2--B2); draw(B1--A3--B2); label("$A_1$",A1,S); label("$A_2$",A2,S); label("$A_3$",A3,S); label("$B_1$",B1,N); label("$B_2$",B2,N); label("1",centroid(A1,B1,I1)); label("2",centroid(B1,I1,I3)); label("3",centroid(B1,B2,I3)); label("4",centroid(A1,A2,I1)); label("5",(A2+I1+I2+I3)/4); label("6",centroid(B2,I2,I3)); label("7",centroid(A2,A3,I2)); label("8",centroid(A3,B2,I2)); dot(A1); dot(A2); dot(A3); dot(B1); dot(B2); [/asy]](https://latex.artofproblemsolving.com/5/6/c/56c4dfb57fc6e7e474f648f52cc8ce4669b2a526.png)
Solution 1
We can use recursion to solve this problem:
1. Fix 7 points on ![]() , then put one point
, then put one point ![]() on
on ![]() . Now, introduce a function
. Now, introduce a function ![]() that indicates the number of regions created, where x is the number of points on
that indicates the number of regions created, where x is the number of points on ![]() . For example,
. For example, ![]() because there are 6 regions.
because there are 6 regions.
2. Now, put the second point ![]() on
on ![]() . Join
. Join ![]() and
and ![]() will create
will create ![]() new regions (and we are not going to count them again), and split the existing regions. Let's focus on the spliting process: line segment formed between
new regions (and we are not going to count them again), and split the existing regions. Let's focus on the spliting process: line segment formed between ![]() and
and ![]() intersect lines
intersect lines ![]() ,
, ![]() , ...,
, ..., ![]() at
at ![]() points
points ![]() creating
creating ![]() regions (we already count one region at first), then
regions (we already count one region at first), then ![]() points
points ![]() creating
creating ![]() regions (we already count one region at first), 4 points, etc. So, we have:
regions (we already count one region at first), 4 points, etc. So, we have:![]()
3. If you still need one step to understand this: ![]() and
and ![]() will still create
will still create ![]() new regions. Intersecting
new regions. Intersecting![]()
![]()
![]()
![]() at
at ![]() points, creating
points, creating ![]() regions, etc. Thus, we have:
regions, etc. Thus, we have:![]()
Yes, you might already notice that:![]()
5. (Finally) we have ![]() , and
, and ![]() . Therefore, the answer is
. Therefore, the answer is ![]() .
.
Note: we could deduce a general formula of this recursion: ![]() , where
, where ![]() is the number of points on
is the number of points on ![]() .
.
~DSAERF-CALMIT (https://binaryphi.site)
Solution 2
We want to derive a general function ![]() that indicates the number of bounded regions. Observing symmetry, we know this is a symmetric function about
that indicates the number of bounded regions. Observing symmetry, we know this is a symmetric function about ![]() and
and ![]() . Now let's focus on
. Now let's focus on ![]() , which is the difference caused by adding one point to the existing
, which is the difference caused by adding one point to the existing ![]() points of line
points of line ![]() . This new point, call it #m, when connected to point #1 on
. This new point, call it #m, when connected to point #1 on ![]() , crosses
, crosses ![]() lines, thus making additional
lines, thus making additional ![]() bounded regions; when connected to point #2 on
bounded regions; when connected to point #2 on ![]() , it crosses
, it crosses ![]() lines, thus making additional
lines, thus making additional ![]() bounded regions; etc. By simple algebra/recursion methods, we see
bounded regions; etc. By simple algebra/recursion methods, we see
![]()
Notice ![]() . Not very difficult to figure out:
. Not very difficult to figure out:
![]()
The fact that ![]() makes us more confident about the formula. Now plug in
makes us more confident about the formula. Now plug in ![]() , we get the final answer of
, we get the final answer of ![]() .
.
Problem10
Find the remainder when![\[\binom{\binom{3}{2}}{2} + \binom{\binom{4}{2}}{2} + \dots + \binom{\binom{40}{2}}{2}\]](https://latex.artofproblemsolving.com/8/d/2/8d24022c5c24f244417fc52eecd6c4daacd8d356.png) is divided by
is divided by ![]() .
.
Solution
To solve this problem, we need to use the following result:
![\[ \sum_{i=n}^m \binom{i}{k} = \binom{m+1}{k+1} - \binom{n}{k+1} . \]](https://latex.artofproblemsolving.com/8/9/2/892527bd79ffaa0fb43c423064a350b1641b25b3.png)
Now, we use this result to solve this problem.
We have
Therefore, modulo 1000,  .
.
~Steven Chen (www.professorchenedu.com)
Solution 2 (similar to solution 1)
Doing simple algebra calculation will give the following equation:
Next, by using Hockey-Stick Identity, we have:![\[3 \cdot \sum_{i=3}^{40} \binom{n+1}{4} = 3 \binom{42}{5} = 42 \cdot 41 \cdot 39 \cdot 38\]](https://latex.artofproblemsolving.com/c/c/e/cce56023c37c307c15590338541b2a101f28e738.png)
![]()
~DSAERF-CALMIT (https://binaryphi.site)
Solution 3
Since ![]() seems like a completely arbitrary number, we can use Engineer's Induction by listing out the first few sums. These are, in the order of how many terms there are starting from
seems like a completely arbitrary number, we can use Engineer's Induction by listing out the first few sums. These are, in the order of how many terms there are starting from ![]() term:
term: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Notice that these are just
. Notice that these are just  ,
,  ,
,  ,
,  ,
,  ,
,  . It's clear that this pattern continues up to
. It's clear that this pattern continues up to ![]() terms, noticing that the "indexing" starts with
terms, noticing that the "indexing" starts with ![]() instead of
instead of ![]() . Thus, the value of the sum is
. Thus, the value of the sum is  .
.
~A1001
Problem11
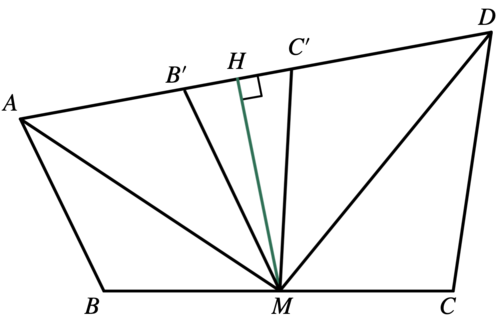
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() ,
, ![]() , and
, and ![]() such that the bisectors of acute angles
such that the bisectors of acute angles ![]() and
and ![]() intersect at the midpoint of
intersect at the midpoint of ![]() . Find the square of the area of
. Find the square of the area of ![]() .
.
Solution 1
According to the problem, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Because ![]() is the midpoint of
is the midpoint of ![]() , we have
, we have ![]() , so:
, so:![]()
Then, we can see that ![]() is an isosceles triangle with
is an isosceles triangle with ![]()
Therefore, we could start our angle chasing: ![]() .
.
This is when we found that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are on a circle. Thus,
are on a circle. Thus, ![]() . This is the time we found that
. This is the time we found that ![]() .
.
Thus, ![]()
Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() .
. ![]() .
.
The area of this quadrilateral is the sum of areas of triangles:![]()
![]()
![]()
![]()
Finally, the square of the area is ![]()
~DSAERF-CALMIT (https://binaryphi.site)
Solution 2
Denote by ![]() the midpoint of segment
the midpoint of segment ![]() . Let points
. Let points ![]() and
and ![]() be on segment
be on segment ![]() , such that
, such that ![]() and
and ![]() .
.
Denote ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Denote ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() . Hence,
. Hence, ![]() and
and ![]() . Hence,
. Hence, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() . Hence,
. Hence, ![]() and
and ![]() . Hence,
. Hence, ![]() .
.
Because ![]() is the midpoint of segment
is the midpoint of segment ![]() ,
, ![]() . Because
. Because ![]() and
and ![]() ,
, ![]() . Thus,
. Thus, ![]() . Thus, \[ \alpha + \theta = \beta + \phi . \hspace{1cm} (1) \]
. Thus, \[ \alpha + \theta = \beta + \phi . \hspace{1cm} (1) \]
In ![]() ,
, ![]() . In addition,
. In addition, ![]() . Thus, \[ \alpha + \beta = \theta + \phi . \hspace{1cm} (2) \]
. Thus, \[ \alpha + \beta = \theta + \phi . \hspace{1cm} (2) \]
Taking ![]() , we get
, we get ![]() . Taking
. Taking ![]() , we get
, we get ![]() .
.
Therefore, ![]() .
.
Hence, ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() .
.
In ![]() , by applying the law of cosines,
, by applying the law of cosines, ![]() . Hence,
. Hence, ![]() . Hence,
. Hence, ![]() .
.
Therefore, \begin{align*} {\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\ & = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\ & = 6 \sqrt{5} . \end{align*}
Therefore, the square of ![]() is
is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Problem12
Let ![]() and
and ![]() be real numbers with
be real numbers with ![]() and
and ![]() such that
such that![]() Find the least possible value of
Find the least possible value of ![]()
Solution
Denote ![]() .
.
Because ![]() ,
, ![]() is on an ellipse whose center is
is on an ellipse whose center is ![]() and foci are
and foci are ![]() and
and ![]() .
.
Hence, the sum of distance from ![]() to
to ![]() and
and ![]() is equal to twice the major axis of this ellipse,
is equal to twice the major axis of this ellipse, ![]() .
.
Because ![]() ,
, ![]() is on an ellipse whose center is
is on an ellipse whose center is ![]() and foci are
and foci are ![]() and
and ![]() .
.
Hence, the sum of distance from ![]() to
to ![]() and
and ![]() is equal to twice the major axis of this ellipse,
is equal to twice the major axis of this ellipse, ![]() .
.
Therefore, ![]() is the sum of the distance from
is the sum of the distance from ![]() to four foci of these two ellipses. To make this minimized,
to four foci of these two ellipses. To make this minimized, ![]() is the intersection point of the line that passes through
is the intersection point of the line that passes through ![]() and
and ![]() , and the line that passes through
, and the line that passes through ![]() and
and ![]() .
.
The distance between ![]() and
and ![]() is
is ![]() .
.
The distance between ![]() and
and ![]() is
is ![]() .
.
Hence, ![]() .
.
Therefore, ![]()
~Steven Chen (www.professorchenedu.com)
Problem13
There is a polynomial ![]() with integer coefficients such that
with integer coefficients such that![]() holds for every
holds for every ![]() Find the coefficient of
Find the coefficient of ![]() in
in ![]() .
.
Solution 1
Because ![]() , we have
, we have
Denote by ![]() the coefficient of
the coefficient of ![]() . Thus,
. Thus,
Now, we need to find the number of nonnegative integer tuples ![]() that satisfy
that satisfy![]()
Modulo 2 on Equation (1), we have ![]() . Hence, we can write
. Hence, we can write ![]() . Plugging this into (1), the problem reduces to finding the number of nonnegative integer tuples
. Plugging this into (1), the problem reduces to finding the number of nonnegative integer tuples ![]() that satisfy
that satisfy![]()
Modulo 3 on Equation (2), we have ![]() . Hence, we can write
. Hence, we can write ![]() . Plugging this into (2), the problem reduces to finding the number of nonnegative integer tuples
. Plugging this into (2), the problem reduces to finding the number of nonnegative integer tuples ![]() that satisfy
that satisfy![]()
Modulo 5 on Equation (3), we have ![]() . Hence, we can write
. Hence, we can write ![]() . Plugging this into (3), the problem reduces to finding the number of nonnegative integer tuples
. Plugging this into (3), the problem reduces to finding the number of nonnegative integer tuples ![]() that satisfy
that satisfy![]()
Modulo 7 on Equation (4), we have ![]() . Hence, we can write
. Hence, we can write ![]() . Plugging this into (4), the problem reduces to finding the number of nonnegative integer tuples
. Plugging this into (4), the problem reduces to finding the number of nonnegative integer tuples ![]() that satisfy
that satisfy![]()
The number of nonnegative integer solutions to Equation (5) is  .
.
~Steven Chen (www.professorchenedu.com)
Solution 2
We know that  . Applying this, we see that
. Applying this, we see that![]() The last factor does not contribute to the
The last factor does not contribute to the ![]() term, so we can ignore it. Thus we only have left to solve the equation
term, so we can ignore it. Thus we only have left to solve the equation ![]() , and we can proceed from here with Solution 1.
, and we can proceed from here with Solution 1.
~MathIsFun286
Problem14
For positive integers ![]() ,
, ![]() , and
, and ![]() with
with ![]() , consider collections of postage stamps in denominations
, consider collections of postage stamps in denominations ![]() ,
, ![]() , and
, and ![]() cents that contain at least one stamp of each denomination. If there exists such a collection that contains sub-collections worth every whole number of cents up to
cents that contain at least one stamp of each denomination. If there exists such a collection that contains sub-collections worth every whole number of cents up to ![]() cents, let
cents, let ![]() be the minimum number of stamps in such a collection. Find the sum of the three least values of
be the minimum number of stamps in such a collection. Find the sum of the three least values of ![]() such that
such that ![]() for some choice of
for some choice of ![]() and
and ![]() .
.
Solution 1
Notice that we must have ![]() , otherwise
, otherwise ![]() cent stamp cannot be represented. At least
cent stamp cannot be represented. At least ![]() numbers of
numbers of ![]() cent stamps are needed to represent the values less than
cent stamps are needed to represent the values less than ![]() . Using at most
. Using at most ![]() stamps of value
stamps of value ![]() and
and ![]() , it can have all the values from
, it can have all the values from ![]() to
to ![]() cents. Plus
cents. Plus ![]() stamps of value
stamps of value ![]() , every value up to
, every value up to ![]() can be represented. Therefore using
can be represented. Therefore using ![]() stamps of value
stamps of value ![]() ,
, ![]() stamps of value
stamps of value ![]() , and
, and ![]() stamps of value
stamps of value ![]() , all values up to
, all values up to ![]() can be represented in sub-collections, while minimizing the number of stamps.
can be represented in sub-collections, while minimizing the number of stamps.
So, ![]() ,
, ![]()
![]() . We can get the answer by solving this equation.
. We can get the answer by solving this equation.
![]()
![]()
![]() ,
, ![]() or
or ![]()
![]()
![]() ,
, ![]()
For
,
,

,

For
,

,

,
, no solution

,

,
or
, neither values satisfy
, no solution

,

,


,

,

The ![]() least values of
least values of ![]() is
is ![]() ,
, ![]() ,
, ![]() .
. ![]()
~isabelchen
Problem15
Two externally tangent circles ![]() and
and ![]() have centers
have centers ![]() and
and ![]() , respectively. A third circle
, respectively. A third circle ![]() passing through
passing through ![]() and
and ![]() intersects
intersects ![]() at
at ![]() and
and ![]() and
and ![]() at
at ![]() and
and ![]() , as shown. Suppose that
, as shown. Suppose that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is a convex hexagon. Find the area of this hexagon.
is a convex hexagon. Find the area of this hexagon.![[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*red+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]](https://latex.artofproblemsolving.com/7/4/a/74a9883958ea503b78cb2c07bc71aefe4d830ce9.png)
Solution 1
First observe that ![]() and
and ![]() . Let points
. Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() , respectively, about the perpendicular bisector of
, respectively, about the perpendicular bisector of ![]() . Then quadrilaterals
. Then quadrilaterals ![]() and
and ![]() are congruent, so hexagons
are congruent, so hexagons ![]() and
and ![]() have the same area. Furthermore, triangles
have the same area. Furthermore, triangles ![]() and
and ![]() are congruent, so
are congruent, so ![]() and quadrilateral
and quadrilateral ![]() is an isosceles trapezoid.
is an isosceles trapezoid.![[asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Bp = dir(105), Ap = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Bp--Ap--O1--C--D--O2--cycle); label("$B'$",Bp,dir(origin--Bp)); label("$A'$",Ap,dir(origin--Ap)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Bp--D^^Ap--C,linetype("2 2")); [/asy]](https://latex.artofproblemsolving.com/8/d/7/8d777e11cf1e82712d37d5839537f1b3d5e93c03.png) Next, remark that
Next, remark that ![]() , so quadrilateral
, so quadrilateral ![]() is also an isosceles trapezoid; in turn,
is also an isosceles trapezoid; in turn, ![]() , and similarly
, and similarly ![]() . Thus, Ptolmey's theorem on
. Thus, Ptolmey's theorem on ![]() yields
yields ![]() , whence
, whence ![]() . Let
. Let ![]() . The Law of Cosines on triangle
. The Law of Cosines on triangle ![]() yields
yields![]() and hence
and hence ![]() . Thus the distance between bases
. Thus the distance between bases ![]() and
and ![]() is
is ![]() (in fact,
(in fact, ![]() is a
is a ![]() triangle with a
triangle with a ![]() triangle removed), which implies the area of
triangle removed), which implies the area of ![]() is
is ![]() .
.
Now let ![]() and
and ![]() ; the tangency of circles
; the tangency of circles ![]() and
and ![]() implies
implies ![]() . Furthermore, angles
. Furthermore, angles ![]() and
and ![]() are opposite angles in cyclic quadrilateral
are opposite angles in cyclic quadrilateral ![]() , which implies the measure of angle
, which implies the measure of angle ![]() is
is ![]() . Therefore, the Law of Cosines applied to triangle
. Therefore, the Law of Cosines applied to triangle ![]() yields
yields
Thus ![]() , and so the area of triangle
, and so the area of triangle ![]() is
is ![]() .
.
Thus, the area of hexagon ![]() is
is ![]() .
.
~djmathman
Solution 2
Denote by ![]() the center of
the center of ![]() . Denote by
. Denote by ![]() the radius of
the radius of ![]() .
.
We have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are all on circle
are all on circle ![]() .
.
Denote ![]() . Denote
. Denote ![]() . Denote
. Denote ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
In ![]() ,
,![]()
Hence,![]()
In ![]() ,
,
Hence,![]()
In ![]() ,
,
Hence,![]()
Taking ![]() , we get
, we get ![]() . Thus,
. Thus, ![]() .
.
Taking these into (1), we get ![]() . Hence,
. Hence,
Hence, ![]() .
.
In ![]() ,
,![]()
In ![]() , by applying the law of sines, we get
, by applying the law of sines, we get![]()
Because circles ![]() and
and ![]() are externally tangent,
are externally tangent, ![]() is on circle
is on circle ![]() ,
, ![]() is on circle
is on circle ![]() ,
,
Thus, ![]() .
.
Now, we compute ![]() and
and ![]() .
.
Recall ![]() and
and ![]() . Thus,
. Thus, ![]() .
.
We also have
Thus,
Therefore,
~Steven Chen (www.professorchenedu.com)


早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1