USACO比赛2021年1月铜组考试真题解析+考试入口！

随着近几年来出国留学的人越来越多,申本的难度也随之不断提高,学生们要有突出的基础成绩,还要有过硬的“软实力”,才能被名校所青睐。而受全球疫情的影响,准留学生们提升软实力的机会有所减少,海外项目不能参加,国内部分活动不能顺利开展。

那么现阶段有什么学术活动活动,既提升学生的综合能力又能被名校认可,而且国内学生足不出国就能参加。所以小编今天必须来给大家介绍一下：USACO全称USA Computing Olympiad，美国信息学奥林匹克学术活动。

比赛时间：3 月 25 日-3 月 28 日

比赛入口：usaco.org

报名时间：无需提前报名，赛时登录账号即可答题

比赛形式：线上

报名费：无

获取备赛计划，考前查缺补漏、重点冲刺

【免费领取】相关真题及解析，还有不定期的高能讲座等你来参加！

以下是USACO比赛2021年1月铜组考试真题：第3题，一起来感受下难度吧~

题目解析

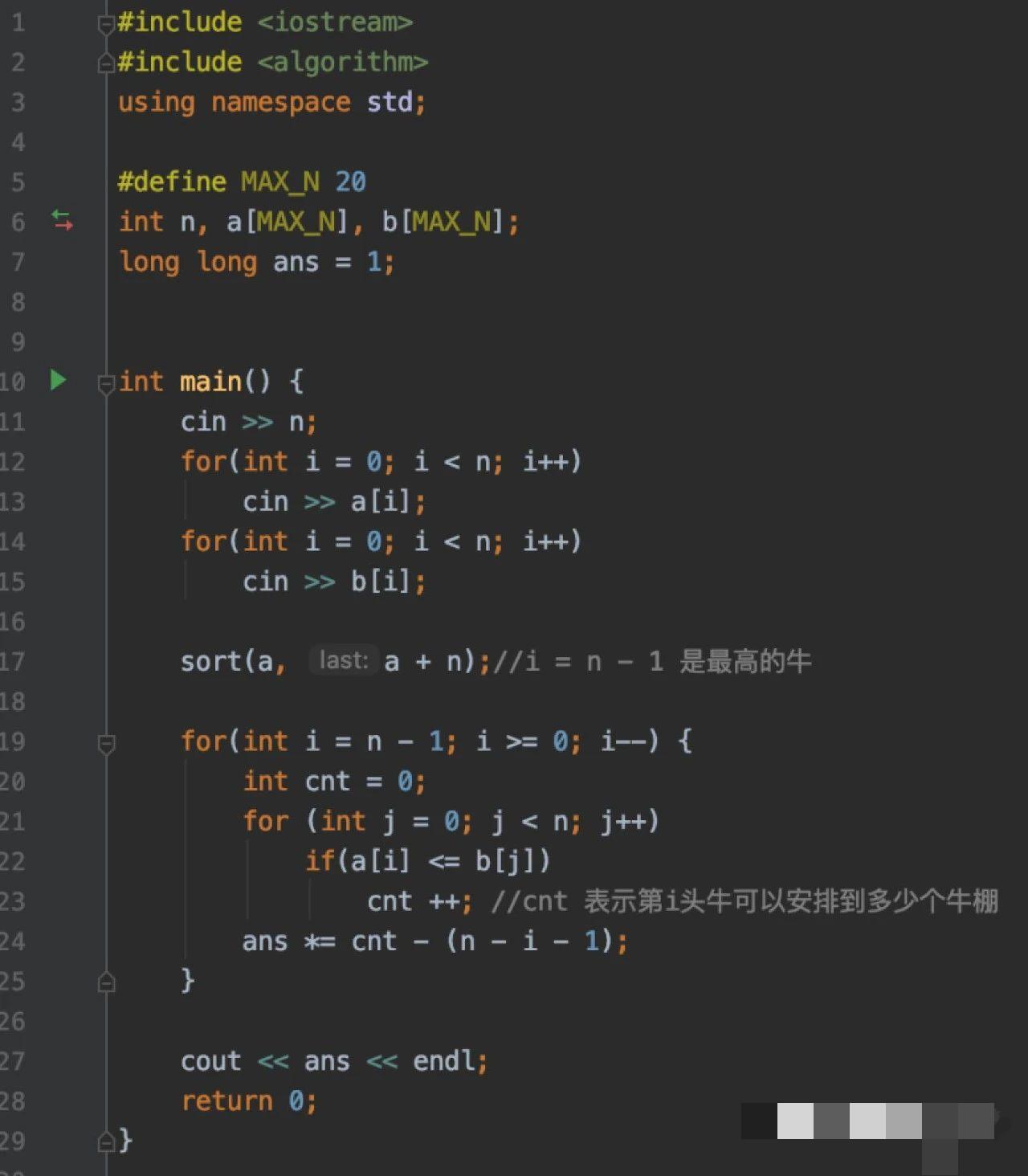
N最大为20，直接枚举的复杂度为O(N*N!)，测试点1-5可以采用直接枚举，当N比较大时显然会超时。

采用排列组合和乘法原理可以以较小的复杂度解此题。

以样例为例：奶牛的高度可以从高到低排序：4 3 2 1，高度为4的奶牛可以安排到2个高度为4的牛棚，因而有2种可能性。高度为3的奶牛可以安排到2个高度为4的牛棚和1个高度为3的牛棚，因而有3种可能性，但由于可以安排高度为4的奶牛的牛棚一定可以安放高度为3的奶牛，这3种可能性中必定有1个用于安放高度为4的奶牛，则最终可能性为3-1=2。同理，高度为2的奶牛可以安排到4个牛棚中，但其中一个用于安放高度为4的奶牛，一个用于安放高度为3的奶牛，则最终可能性为4-1-1=2。高度为1的奶牛也可以安排到4个牛棚中，但一个用于安放高度4，一个用于安放高度3，一个用于安放高度2，则最终可能性为4-1-1-1=1。最后根据乘法原理，安排4头奶牛的方法数为：2*(3-1)*(4-2)*(4-3)=8。该方法的时间复杂度为O(N^2)。

解法代码

如果改进，时间复杂度还可以优化到O(N*logN)，只是本题的N很小，区别不大。代码如下，可以思考下原因。

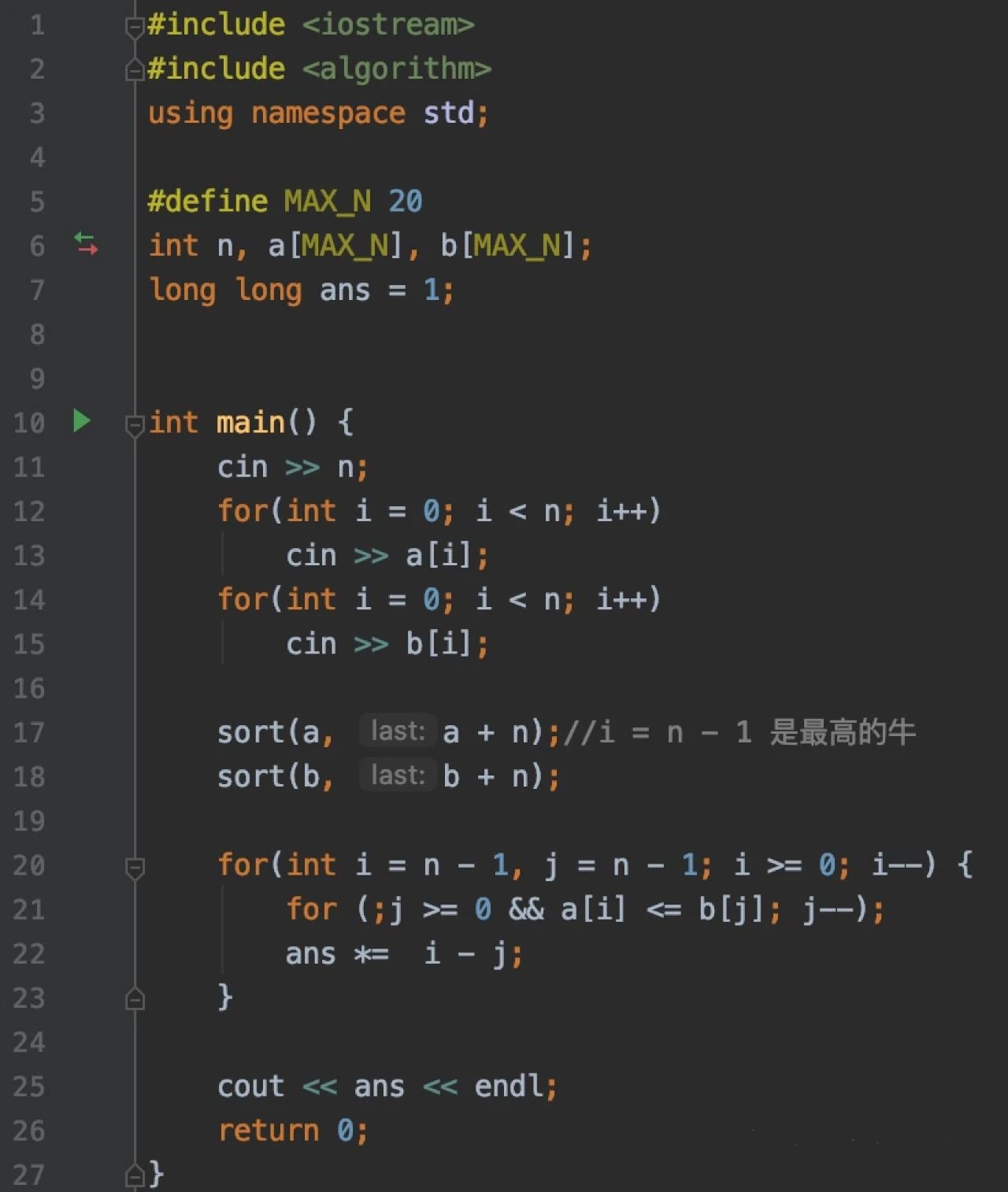
USACO学术活动成本低，收益大，见效快！是一个非常值得参与的学术活动哦~