A-Level数学中导数的除法法则运用

数学是一门研究数字、数量、形状、空间及它们之间关系等等的庞大学科，这门课有大量的领域和分支，是当今许多科学技术的基础。数学一般分为纯数和应用数学，前者研究的是完全抽象的对象，而后者关注的是数学在现实生活中的应用。

A-level数学将帮助学生理解基本的数学概念和思想，拓展计算技能和解决问题的能力，这些都是进入高等教育和未来职业生涯所必需的。今天我们分享的是A-Level数学中导数的除法法则运用。

和乘法法则类似，微分除法法则适用于求由两个或几个函数的商函数的导数，也就是对函数f（x）=g（x）/h（x）进行求导，或者表达为对y=u/v进行求导，其中u和v都是关于x的函数。

关于这类函数的求导，我们可以利用之前学习过的链式法则和乘法法则进行推导：

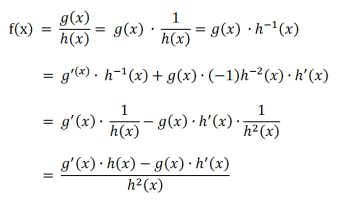
Step1：将函数改写成便于求导的指数形式；

Step2：利用Product Rule和Chain Rule对函数进行求导；

Step3：整理函数，写成分数的形式；

Step4：通分，将分母统一化成h²（x），得到最终结果。

总结：微分除法法则如下，可以写成两种形式：

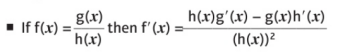
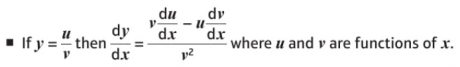
记忆的方法也和之前Product Rule类似，我们可以编个小口诀，“上导下不导，减去，下导上不导，整体除以下面函数的平方”。再结合之前的学习，无论这个分式方程的分子和分母是由多少个函数组成，我们都可以对式子进行求导。

Question 1：

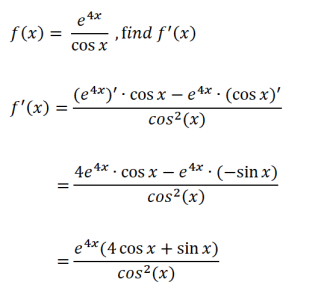
学会微分除法法则，分式求导是不是so easy，那么，下面我们稍稍提升点难度！

Question 2：

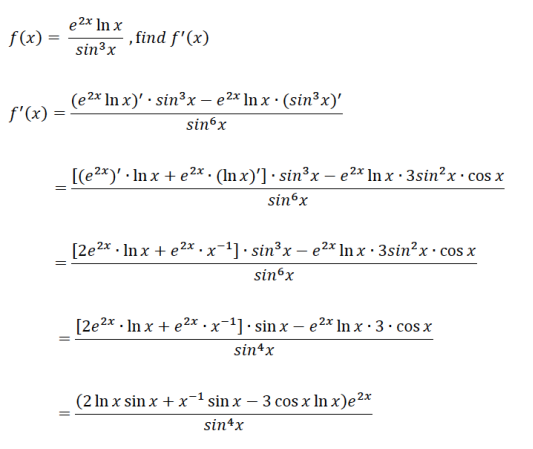
结合了微分法则三巨头的题目还是有点难度吧，但只要掌握公式和方法，逐层运算，就可以轻松击破。

最后，在P3的考试中我们见到的函数求导基本都会是将多重法则（Chain Rule,Product Rule,Quotient Rule）的综合运用，大家一定要熟练掌握。

需要针对A-level考试辅导提升的同学，欢迎扫码详细咨询~

还能【免费领取】相关真题及解析！