解密剑桥大学最难笔试 – STEP（下）

相信大家看完 解密剑桥大学最难笔试 – STEP（上）已经对STEP有了直观的认识，这篇STEP（下）给同学们带来纯干货分享！

李老师教了5年STEP，每年都能看到学生的剑桥之梦止步于STEP考试，甚至有学生辛辛苦苦拿到了剑桥的OFFER，可是条件确是STEP II和III的Double S，也是心疼这位学生一秒钟。其实STEP考试虽然变态难，但并非无解，今天李老师就来重点剖析一下STEP考试中常见的套路，以及有效的解决办法，给大家平时的学习备考中提一些建议。

STEP有哪些常见套路？

套路1：参数化

相较于A-LEVEL题目的具体问题，STEP更喜欢直接根据参数找到一个general result，并看特定参数下的应用。如以下这题：

 套路2：相关性

从上题也可看出STEP题的另外一个特征：前后题目相关性很强，即用前面小问的结论做后面的问题。有时会有’hence’,’therefore’等关键词作提示。如上题，只要用心观察找对几个参数的值，这题就能引刃而解。有时题目不会明说，但是考生也得细心观察找出前后联系。下题是另一个例子：

李老师点评：只需细心观察前后两小问积分上下限便可知第二小问实际就是第一小问。

套路3：老公式新用

在A-LEVEL旧有的公式上进行新的应用，比如学生很熟悉的 sin (x+y) = sin (x) cos (y) + cos (x) sin (y) ，STEP不考这个，而是要求考生应用由他推导出来的和差化积或积化和差公式，并在此基础上进行证明。比如下面这题的第一个证明：

套路4：大学数学提前考

STEP喜欢先介绍一个新的概念（基本来自于大学数学）并要求学生马上会用。比如下题的Chebyshev’s  Inequality：

李老师点评：考新知识点时，题目有时会给提示，但是提示比A-LEVEL少，并进一步要求学生完全理解提示的意义找到新的更隐蔽的Hint（真是套路深啊!）。

下题就是一个典型： 第一小问直接给提示 Use the subsitution of y = u x，第二小问用第一小问的代换，第三小问的代换需要根据前两题的解题过程的特点（隐藏Hint）来找。

套路5：计算量大

例如Integration by parts的知识点在会使用两次或更多。对于习惯了用一次公式就得出结论的A-LEVEL学生来讲，思想上准备往往不充分，容易自我怀疑而半途而废，请看下题的第二小问：

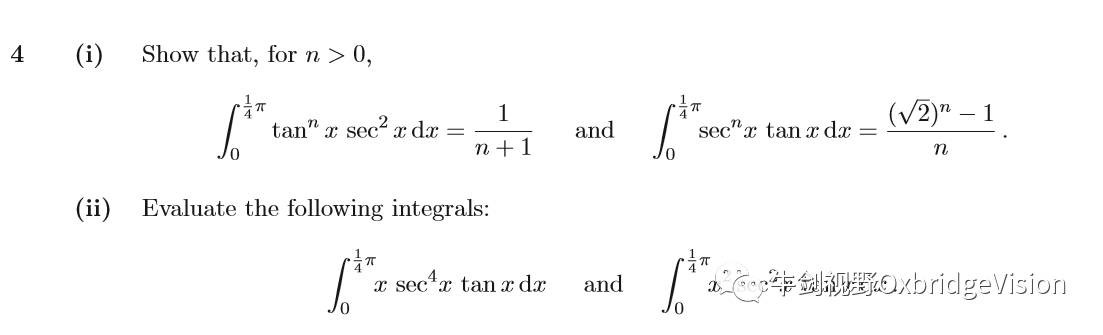
李老师点评：这时候你要想相信自己的判断。

套路6：综合题居多

例如下题，表面上是个概率的题目，但实际上要证明数论的一个结论。

李老师点评：像该类综合题，在考察学生运算能力的同时，更是综合能力的检测。

套路7：力学题计算复杂

对于力学题，通常概念简单，但是计算（Algebra）比较复杂。对于不想多动脑筋，但是计算能力强的考生可以考虑多做力学题目。如下面这一题，是普通的一个Projectile情况稍稍变形一下，只需计算找出最晚落地的子弹并计算就可。

套路8：概率题刁钻

对于概率和统计：STEP I和II考试偏向于概率，概率比较多变，在很多情景中都可以考到。

套路9：统计题偏理论

STEP III第三部分偏向于统计理论，有较多大学统计理论的内容，然而没有概率题灵活。下一题就是普通的一道大学统计理论题：

你该如何反套路？

1. 选题很关键

首选画图题，通常都有相应的步骤来作图，逻辑清楚，简单明了

次选力学题，尤其是动量冲量和抛射体的题，题型单一，变化较少

至于数论的题千变万化，可以选择放弃

2. ‘STEPISATION’

平时做A-LEVEL练习的时候，可以尝试着将题目“STEP化“来练习。比如以下这道很普通的A-LEVEL题目：

相信这题大家都会解答，如果把题目改写成’Use the binomial expansion, in ascending powers of of 1/ (sqt (1-2x)) to find an approximation to sqt (10) ’, 这样改写之后就可以作为一道STEP中的一小问。

3. 千万别凑题

注重做题的完整性。和大学数学一样，STEP更追求的是精而非广。试卷第一页的考试注意事项上的这两句话需要得到更多的重视：

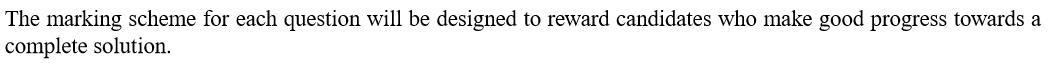
4. 条件与结论平等

要牢记，题目给出的条件和我们需要证明的结论是等价的。我们可以尝试用结论反着推，尝试找到与条件相似的形式，并用条件尝试推导到此形式，最后从头开始，用条件开始在新的一页纸上推导到结论。即使条件和结论不是互推的，也要不断问自己结论的之前一步是什么，并不断变形，不断往条件靠拢，直到他们Converge为止。

总而言之

首先了解到自己目标学校目标专业对STEP的要求，根据要目标来制定计划。如目标OFFER的STEP要求较低（比如2），可在保证正确率的前提下少做两题。

早准备，充分准备。把题型分类：必做题，选做题和不做题。最重要的是找出适合自己的知识点及题型并不断练习，最大化必做题得分。

可根据Past papers，找出新的知识点，并自学，或适当自学部分大学数学，把部分新知识变成熟悉的知识。