Alevel物理-油滴测量基本电荷的电荷量实验介绍

罗伯特.密立根是1923年诺贝尔物理学奖得主。1910-1917年曾以油滴实验精确地测得了基本电荷的电荷量的值，从而确定了电荷的不连续性。

油滴测量基本电荷的电荷量

在20世纪初，物理学家对于电荷是否连续产生了争论，一部分科学家认为电荷是连续的，就如一般意义上我们理解时间或者长度一样，可以无限进行细分；但是另一部分科学家认为电荷是离散的，存在有一个不可进一步细分的基本电荷量。围绕着这个争论，密立根和哈维.弗莱彻设计了一个实验来对这两种理论进行检验。实验的设计（图1.）简化版本如下图所示：

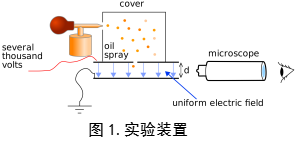
总体来讲，其流程可以概括为利用带电粒子在电场中受力的特性，用已知的电场强度推算带电物体的电荷量，再通过寻找不同的电荷量之间的关系来发现他们是否连续。下面让我们来详细的介绍整个的实验流程。之所以叫做油滴实验，因为第一步我们需要利用一个特定的装置（图2.）制造油滴。

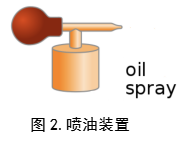
这里的油滴并不是一般意义上我们认为的那种从壶里面倒出来的一整滴，而应该是类似于一个喷雾装置喷出的雾中的一个小液滴，其体积是非常非常之小的。在喷出的过程中，由于跟喷嘴的摩擦，部分油滴就有可能带上电荷，当然，也可以使用X光照射这些油滴使它们带上电。

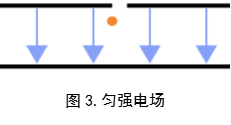
之后，我们需要让这些带电油滴降落到一个匀强电场（图3.）的环境中，由于油滴带电，在匀强电场中油滴会受到力的作用，假如两平行极板之间的距离是定值，电势差可以调节，那么根据公式我们就可以调节匀强电场的电场强度E。对于一个电荷量为q的粒子，在一个电场强度为E的匀强电场中，其受力可以通过公式F=qE来进行计算。而又因为在电场中的油滴只受到重力和电场力的作用，所以如果这两个力大小相等方向相反，那么油滴受到的合外力就会变成0，油滴就可以静止在匀强电场中。也就是说，对于一个处于平衡状态的油滴来讲，我们总是有其中，重力加速度g，两极板之间的电势差V和两极板之间的距离d都是可以直接得到的，也就意味着只要我们可以得到油滴质量m，那么就可以利用上面的公式计算出油滴上面的电荷量q。

在实际操作这个实验的时候，油滴质量m的测量是一个比较困难的点。在当时并没有能够直接精确测量的方法。所以油滴的质量最终需要通过公式来进行计算，其中为油的密度ρ，V是油滴的体积，而又因为这个极小的油滴以球形存在，所以体积又可以通过球的相关公式，使用半径r 计算得到。那么究竟如何可以确定油滴的半径呢？直接测量是不现实的，一方面是油滴极小，直接测量会产生比较大的百分比不确定性；另一方面则是油滴的形状一旦受到测量仪器的外力影响就无法维持。所以这里采用了一个非常巧妙的方法来完成对其半径的测量。

我们都知道，在流体中运动的物体会受到阻力的作用，如果流体的流动是平流（Laminar Flow），那么阻力的大小就可以使用斯托克斯定理（Stokes’ Law）计算，即F=6πrηv。其中η为流体的粘滞系数，r是小球的半径，v是相对速度。由于物体在流体中下落的时候受到阻力，浮力和重力的三个力的作用，而阻力又会随着速度增加而增加，最终物体会达到一个受力平衡的匀速运动状态，这个最终的速度我们称之为终端速度（Terminal Velocity），可以通过公式来进行计算，其中ρs和ρf分别为小球和流体的密度。也就是说，如果我们让小油滴在空气中到达终端速度并测量出来这个速度，就可以利用上面公式推算油滴的半径了。

再经历了上面的计算过程之后，油滴上面携带的电荷量q也终于可以计算了，我们可以统计带有不同电荷量的油滴的个数，然后将这些信息体现在一张图像上（图4.）。

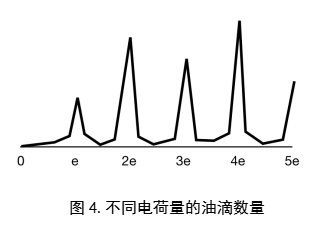
观察可以发现，在某些特定的电荷量上油滴的数量特别多，这就是电荷不连续的证据，对于一个油滴来讲，它只能拥有基本电荷的整数倍电荷。在经历了一系列精密的测量和计算之后，密立根得到了一个1.5924x10-19C的基本电荷量，这与现在被广泛接受的1.6022x10-19C的电荷量非常之接近了。

如果你对 ALEVEL 备考没有思路，对于选什么学术活动没有目标，欢迎前来咨询 雅思托福、夏校，牛剑面试等【免费领取】相关真题及解析！