重磅！斯坦福数学夏校SUMaC开放申请！快来解答2022入学试题吧！

负有盛名的四大数学夏校之一

MIT本科招生推荐夏校活动

体验顶级美国大学的课程

改变对数学的认识，玩转数学！

斯坦福大学数学夏令营  

 Stanford University Mathematics Camp 

2022申请开放！同时公布入学考试题目！

如果你具有强大的数学天赋

想要深入研究数学难题

增加未来申请TOP美本的录取率

SUMaC数学营是你的不二选择！

斯坦福大学数学夏令营SUMaC

斯坦福大学数学夏令营（SUMaC）开始于1994年，由美国数学协会Epsilon基金和斯坦福数学系共同资助，是一个针对高中生数学能力拓展的学术型项目。

官网：sumac.spcs.stanford.edu/

从项目开始1995年招收了第一批共12名学生，至今SUMaC为了保证参与项目的学生都能得到足够多的关注和收获，严格限制每届40人的招生规模。

1.申请时间及项目时间

2022年申请窗口已开放，截止报名时间：2022年3月15日

申请通知书发放：2022年5月

SESSION I：6月21日-7月9日（参考2021年）

SESSION II：7月19日-8月6日（参考2021年）

2.申请要求

● 10或11年级并对数学有特殊兴趣和能力的学生

● 申请材料：学校成绩单、教师推荐信、数学作业样本、以及可选视频文书（强烈推荐）等

3.项目内容

SUMaC项目专注于纯数学，同时提供有高度挑战性的两个系列课程：Program I 的主题是抽象代数和数论，Program II 的主题是代数拓扑学。

4.项目费用

申请费$65，学费$3,250，某些课程可能需要购买额外的材料但不超过$100。

往届参加的学生反馈

“我会向其他高中生强烈推荐 SUMaC，因为它不仅教给学生高中或学术活动数学领域以外的有趣数学主题，而且还因为它向他们展示了如何超越给定的问题进行思考；任何问题都可能导致另一个问题，而通过 SUMaC，我增强对数学的好奇心。”

* 以上分享来源于网络

2022 SUMaC 入学考试题目公布

这些五花八门的“变态”入学考题

小编直呼：完全看不明白！

跪求各位数学大神来解答！

（Stanford：要是你能理解就直接来我们学校吧☹）

Q1

■ Tell us something interesting about the number 2022 or explain why you think it is a completely  uninteresting number. This is a purely subjective open-ended question with no wrong answers.

■  告诉我们一些关于“2022”这个数字有趣的事情，或者如果你认为它很无趣也请解释一下。这是一个纯粹主观的开放式问题，任何答案都可以。

Q2

■ A number ? has the increasing factor property if it can be uniquely factored into a product of strictly  increasing factors, not including the factorization n=1∙ n. That is, n=n1∙n2 ∙ ⋯ ∙ nk for k > 1 and 1 < n1 < n2 < ⋯ < nk < n, and there is no other factorization n = m ∙ m1 ∙m3 ∙ mk with  1 < m1 < m2 < ⋯ < mk < m, such that the sequence m1, m2, … , mk is different than the sequence  n1, n2, … , nk. For example, 6 has the increasing factor property since 6 = 2 ∙ 3, and 2 < 3, and there  are no other factorizations of 6 with strictly increasing factors. 12 does not have this property since it  can be factored into strictly increasing factors in two ways, 12 = 3 ∙ 4 and 12 = 2 ∙ 6. Characterize all positive integers that have the increasing factor property.

■  如果一个数字可以唯一地分解成一系列严格递增的因子的乘积（不包括n=1∙ n这样的基本分解形式），则称它具有递增因子特性。 也就是说，对于k>1，n=n1∙n2 ∙ ⋯ ∙ nk ，并且1<n1<n2 < ⋯ < nk < n，n没有其他分解形式n=m1∙m2 ∙ ⋯ ∙ mk ，1<m1<m2 <  mk < m,使得序列m1，m2，…，mk不同于序列n1，n2，…，nk。

例如，6具有递增因子特性，因为6=2∙ 3同时2<3，并且6没有其他的递增因子分解形式。而12不具有此属性，因为它可以通过两种方式分解为严格递增因子的乘积，12=3∙ 4以及12=2∙ 6。描述所有具有递增因子特性的正整数。

Q3

■ Find a polynomial p(x) with integer coefficients for which 2√3 + 3√2 is a root. That is find p(x)  such that for some positive integer n, and integers a0, a1, a2, … an，

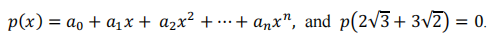
■  试求一个整数系数的多项式p(x) 使得2√3 + 3√2是它的根。也就是说，请找到正整数n和整数a0, a1, a2, … an，使依此构造的多项式p(x)满足下面等式

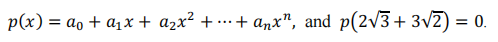
 扫码添加翰林小助手 

 领取完整Admissions Exam版本