Alevel数学—当证明题遇到函数题，怎么解？

Proof 证明题和 Function 函数题是Alevel数学考试中常见考点，官方数据中显示，在二者结合的题型中，考生往往拿不到满分，那我们如何在这类题型中拿到满分呢？

今天要讲的这道题，出现在2019年Alevel 数学Pure Math Paper 1试卷中，正是综合了Proof和Function两个考点的经典真题。虽然此题总共6分，初见并不觉得非常复杂，但令人惊讶的是，当年考生的平均得分只有29%！同学们比较擅长直接运用已经被证明好的结论，因而忽略了如何去证明结论的正确性，这一类的题型往往让同学无法获得满分。

先来一起看看Alevel 数学P1这道题目：

下面，让我们一题一题解：

Question 10(i):

在Part 1中，我们需要证明当时（N: Set of Natural Number/ 自然数），不能够被4整除，由于题目中要求的是证明所有的n都需要满足条件，所以这是一道需要Proof by Exhaustion的题型，因此我们不能直接代入数字举例证明。

我们可以把n的取值分为even number （偶数）和odd number （奇数）：
•When n is even number, n = 2k, where k is an integer （2的倍数皆偶数）

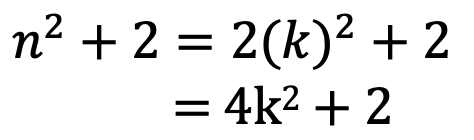
由此我们能得出，当n为偶数时，要比4的倍数多了2，所以不能被4整除
•When n is odd number, n = 2k + 1, where k is an integer（偶数的值加1为奇数）

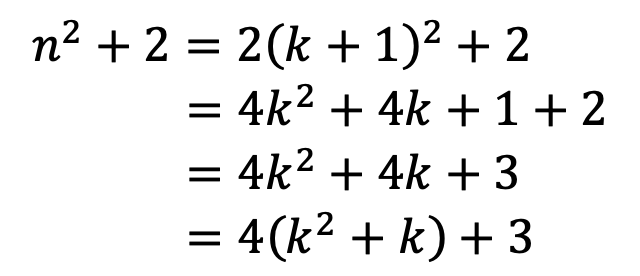
由此我们能得出，当n为奇数时，要比4的倍数多了3，所以同样不能被4整除

综上，我们能得出以下结论：当n为偶数和n为奇数的情况下，都不能被4整除。因此，当（任意自然数）时，都不能被4整除。

Question 10(ii):

Part 2虽然只是一道2分的题目，但是其实相对来说要比Part 1稍微复杂一些，我们的考试局经常喜欢出这种题型，需要同学们判断题干中的Statement是否Always True(总是正确)，Sometimes True(有时候正确)，或者是Never True(错误)。

同学们可以暂停思考一下，如果判断为Always True/ Never True，是一道什么类型的题型呢？
（接着往下看，就能找到答案哦~）

回到题干中提到的Statement，我们需要判断当时，3x – 28的绝对值大于或者等于x - 9的正确性，如果判断为Always True或者Never True，即相当于一道Proof （证明题），与我们Part 1的部分相类似。

第一步

我们可以把Statement文字描述转换成数学的不等式，|3x–28|≥x–9，通过解出此不等式，找到这个Modulus Inequalities的x取值范围，运用Algebraic Method去总结结论：

同学们要注意去掉绝对值符号时，我们需要分为两种情况：

•当3x-28≥0时，解3x-28≥x-9
•当3x-28<0是，解-(3x-28)≥x-9

所以，不等式|3x–28|≥x–9的解是x≥9.5；x ≤9.25

第二步

我们尝试代入在x≥9.5；x≤9.25区间范围之内的值和区间范围之外的值进行验证：

综上所述，我们可以得出以下结论:Hence, the statement is sometimes true.

最后我们也可以运用我们在GCSE/IGCSE中学过的知识点，分别画出y = |3x – 28|和y =  x – 9的图（如下图所示），从而佐证在第二步中得到的结论，一部分的Modulus Graph是大于y = x – 9, 而另一部分是小于y = x – 9的。

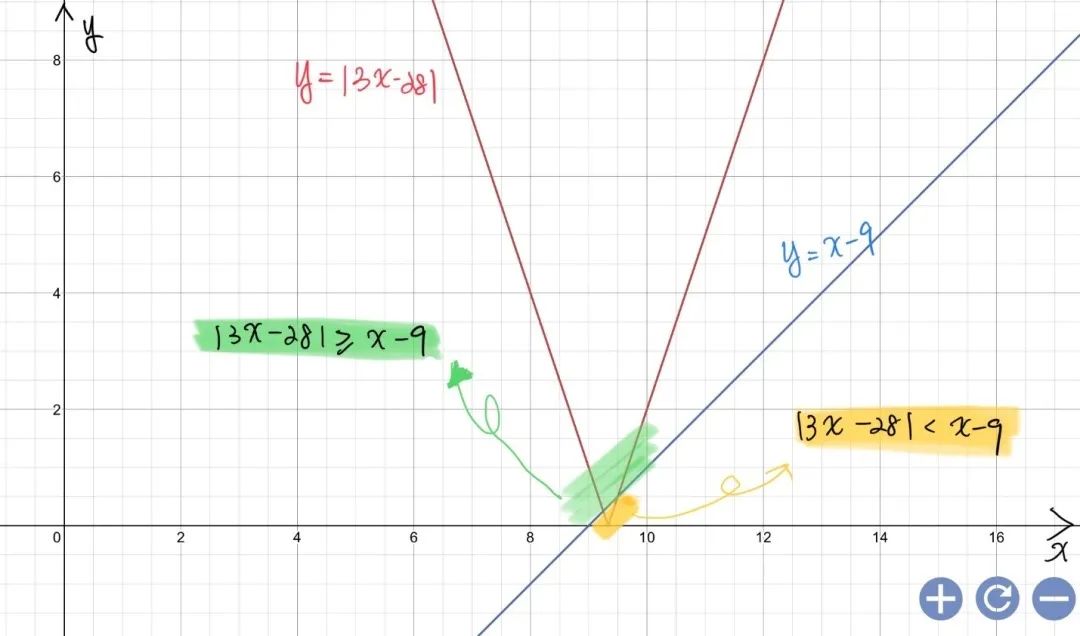
好啦，今天的Alevel数学P1干货就分享到这里！大家有没有学会呢？了解了这类Proof题型的解题方法以后，有没有发现，证明题其实没有想象的那么复杂呢？不要忘记动手实践一遍，找一找相类似的题目，多练习一下吧！这样才能更好的巩固哦~