2022年AMC8来临，掌握这5大思维法，助你攻克AMC排列组合！

在AMC8的考试中，除了有一些可以通过直接计算快速得分的题目，又有一类则是专门用于对学生进行能力分级的题目。而这类题目经常出现在统计学中的排列组合，概率，几何学中的面积体积计算，函数中的特殊符号计算与推理，以及代数中的计数知识点中。

这些知识点的学习都需要一定基础。比如在一般的数学学习体系中，排列组合是在高中阶段才会碰到的知识，并且在AMC考试中还进行了适当的加强，因此是当之无愧的难点知识。

今天就带大家来梳理5大类排列组合的题型以及对应的计算方法，助你彻底攻克这一AMC知识难点。

1.表格法（Counting Using Charts）

在做计数原理的问题时，穷举法都是一个不错的方法。当我们把所有的情况罗列出来的时候，问题就会变得清晰直白。而罗列情况时，比较好用的是表格法和树状图法。其中表格法是出现在两个独立的试验中的情况，例如下题：

Exampie8.Two dice are rolled. How many ways are there to roll a sum of 5?

当出现两个独立的事情同时发生的时候，我们可以将两个事情发生的所有情况分别放在表格的第一行和第一列上（如下图所示），此时这个6*6的表格中的数据，就对应事情发生的所有情形。

而在表格中的数据也变得一目了然，如题干要求中寻找和为5的情况，便可以直接读出有四种可能性。

2.树状图法（Counting Using Tree Diagram）

当出现超过两个事件的情况，表格法便失去了效果，此时就可以采用树状图法。当然树状图法也适用于两个事件的情况，它的应用能力比表格法要更加强大。树状图法是指将事情分为几步，然后在第一步发生的情况下考虑对应的分支情况。

例如下面这道题，选择有多少种方案可以搭配裙子。第一步可以选择颜色，颜色的情况有三种，第二步则是在不同颜色的基础上选择款式，每一种颜色下对应着四种款式，因此应该是3*4=12，选C。

Example 9.A designer has 3 fabric colors he may use for a dress: red, green,and blue. Four different patterns are available for the dress. If each dress design requires one color and one pattern, how many different dress designs are possible?

(A)10 (B)24(C)12(D)14 (E)20 P2

同时如果将这个题目难度系数提高，在不同款式下还可以分为不同的型号，S，M，L。便可以在每个款式后面再分一个树状图，最后的结果是3×4×3=36种。

3.捆绑法（Counting with restriction）

在排队问题中，经常会碰到A与B想要靠在一起的情况，而遇到这样的问题，又该如何计算其中的情况数。其中比较好用的方法为捆绑法，即先将想要靠在一起的人捆绑在一起视为一个整体，而后在进行排列。

Example 12.In how many ways can 5 books be arranged on a shelf if two of the books must remain together, but may be interchanged?

(A)12 B)24 (C)48 (D)96 (E)5

如上题所示，五本书进行排列但必须有两本书靠在一起。大胆的操作一下，可以直接将这两本书粘起来成为一本厚书，由此可以直接当作四本书在进行排列，总情况数为4！，但是两本书粘起来的时候并不一定谁在左谁在右，因此其中有两种情况。总的情况数应该是两个数值相乘，即为4！*2=48，选C。

4.圆桌排列法（Circular Permutations）

圆桌排列是指当被排列的人并不是一条长列，而是考虑坐在一个圆桌上的情况数。圆桌排列与常规排列的区别在于——对于一个圆形而言，只考虑相对位置。例如有ABCD四个人坐在圆桌上，常规排列中的ABCD，BCDA，CDAB，DABC当出现在圆桌上的时候会被视为一种情况，因为四人的相对位置是不变的。因此在处理圆桌排列的时候总情况数应该为4！/4，因此可以直接记作3！。而对于n个人的圆桌排列可以直接记作（n-1）！。

THEOREM 3: The number of circular permutations (arrangements in a circle) of n distinct objects is (n - 1)!.

比如而对于下面的例题18这个题可以直接得到7个人的圆桌排列情况数应该是6！。

Example 18.In how many ways is it possible to seat seven people at a round table?

5. 分配法（Combinations with Repetitions）

在AMC8中经常会出现这样一种题目，小明手上有18个苹果，如果要想将18个苹果分给三个人，而必须保证每个人手上至少有一个苹果，那么总共有多少种情况？

这一类问题可以直接用分配法的公式进行直接计算，对于这样一类问题，可以直接使用下面的公式，即为：
THEOREM 4:Let n be a positive integer. The number of positive integer solutions to X1+X2+…+Xr=n is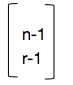
对于上述的分苹果问题，可以直接列式。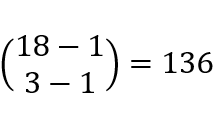
而如果对问题进行升级，同样还是分苹果的问题，但是不用保证每个人手上至少有一个苹果，则可以直接利用下面的公式：

THEOREM 5:Let n be a positive integer. The number of non-negative integer
solutions toy1+y2+…+yr=n is
对于新的分苹果问题，则可以直接写作。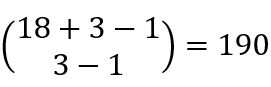

在2019的AMC8的考试中，最后的压轴题就是考察的分配法的问题，这个题在上述公式基础上可以适当进行发散就可以做出来。
Problem25

Alice has 24apples.In how many ways can she share them with Becky and Chris so that each of the people has at least 2apples?
(A)105 (B)114 (C)190 (D)210 (E)380

如上题所示，24个苹果分给三个人，每人至少有两个苹果，其实相对于先分出六个苹果，剩下的18个苹果分给三个人并不用保证每个人的手上有苹果，总情况数为。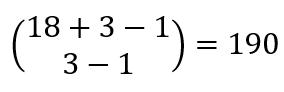

以上就是在AMC 8中经常出现的排列组合类型，在这种题目中，运算不是最重要的，重要的是思考问题的方式。只要思考的方向准确，通过一个算式就可以得到最后的结果，但如果思考不清晰，那便可能思虑很久也得不到有效的结果。

为了帮助同学们吃透排列组合问题，翰林精心准备了习题集给大家，帮助大家巩固这几种方法，大家可以检测一下自己是否掌握了上面这些方法。AMC8学术活动来临，有需要的同学扫码即可免费领取~

 

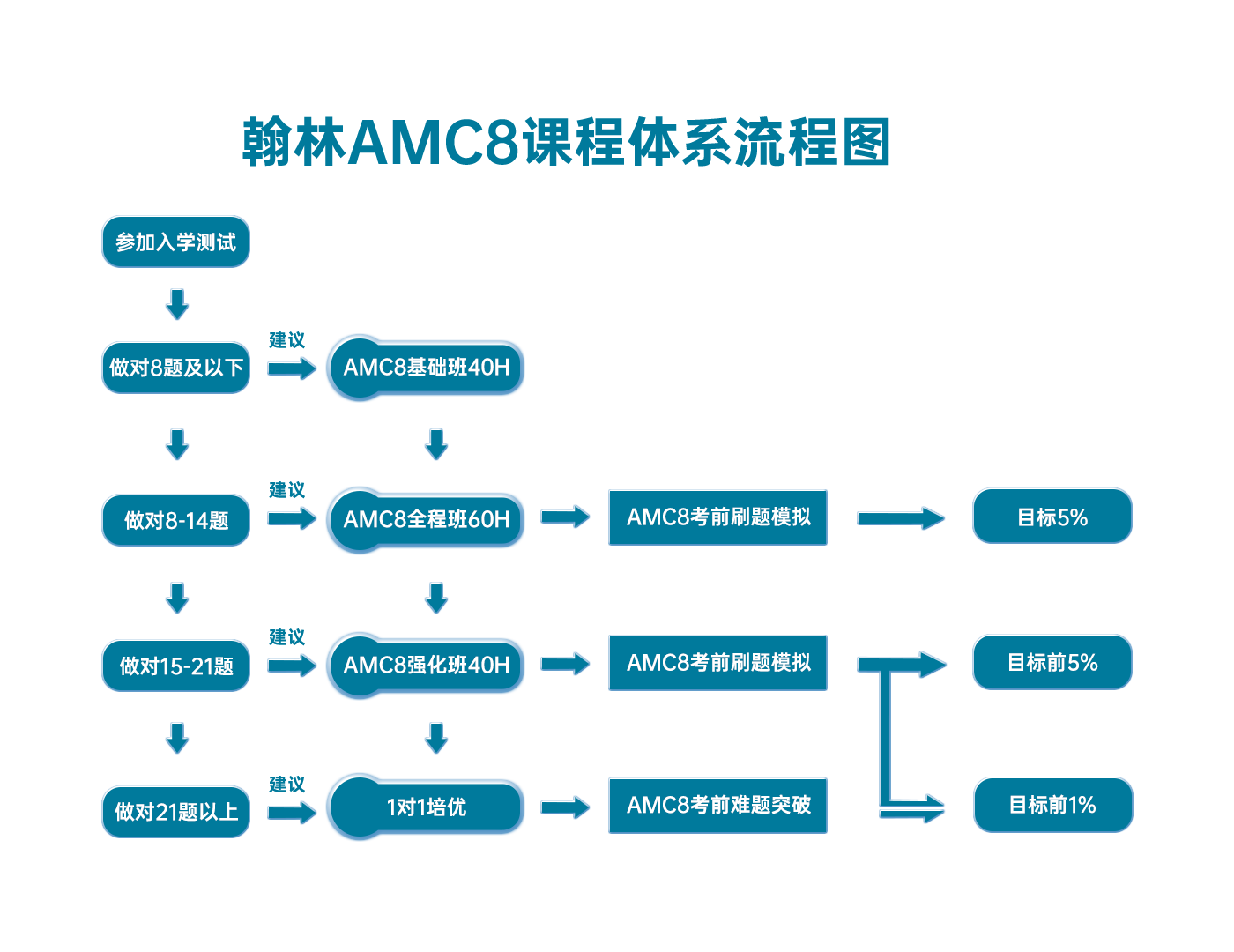
翰林AMC8课程体系流程图