2021年11月AMC10B卷考试真题及解析

2021年11月AMC10B卷考试真题及解析

1. What is the value of 1234 + 2341 + 3412 + 4123?
(A) 10,000 (B) 10,010 (C) 10,110 (D) 11,000 (E) 11,110
E
2. What is the area of the shaded figure shown below?

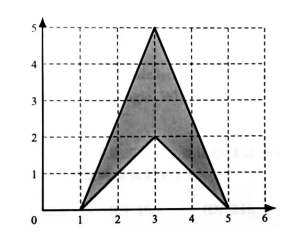
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12
B
3. The expression 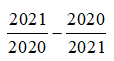is equal to the fraction in which p and q are positive integers whose greatest common divisor is 1. What is p?
(A) 1 (B) 9 (C) 2020 (D) 2021 (E) 4041
E
4. At noon on a certain day, Minneapolis is N degrees warmer than St. Louis. At 4:00 the temperature in Minneapolis has fallen by 5 degrees while the temperature in St. Louis has risen by 3 degrees, at which time the temperatures in the two cities differ by 2 degrees. What is the product of all possible values of N?
(A) 10 (B) 30 (C) 60 (D) 100 (E) 120
C
5. Let . Which of the following is equal to ?
(A) (B) (C) (D) (E)
E
6. The least positive integer with exactly 2021 distinct positive divisors can be written in the form   where m and k are integers and 6 is not a divisor of m. What is m+k?
(A) 47 (B) 58 (C) 59 (D) 88 (E) 90
B
7. Call a fraction , not necessarily in simplest form, special if a and b are positive integers whose sum is 15. How many distinct integers can be written as the sum of two, not necessarily different, special fractions?
(A) 9 (B) 10 (C) 11 (D) 12 (E) 13
C
8. The greatest prime number that is a divisor of 16,384 is 2 because 16,384 =2¹⁴. What is the sum of the digits of the greatest prime number that is a divisor of 16,383?
(A) 3 (B) 7 (C) 10 (D) 16 (E) 22
C
9. The knights in a certain kingdom come in two colors: of them are red, and the rest are blue. Furthermore, of the knights are magical, and the fraction of red knights who are magical is 2 times the fraction of blue knights who are magical. What fraction of red knights are magical?
(A) (B) (C) (D) (E)
C
10. Forty slips of paper numbered 1 to 40 are placed in a hat. Alice and Bob each draw one number from the hat without replacement, keeping their numbers hidden from each other. Alice says, "I can't tell who has the larger number." Then Bob says, "I know who has the larger number." Alice says, "You do? Is your number prime?" Bob replies, "Yes." Alice says, "In that case, if I multiply your number by 100 and add my number, the result is a perfect square." What is the sum of the two n1lmbers drawn from the hat?
(A) 27 (B) 37 (C) 47 (D) 57 (E) 67
A
11. A regular hexagon of side length 1 is inscribed in a circle. Each minor arc of the circle determined by a side of the hexagon is reflected over that side. What is the area of the region bounded by these 6 reflected arcs?
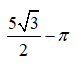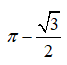(A) (B) (C) (D) (E)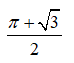
B
12. Which of the following conditions is sufficient to guarantee that integers x, y, and z satisfy the equation
x(x-y)+y(y-2)+z(z-x)=1?
(A) x>y and y=z (B) x=y-1 and y=z-1 (C) x=z+1 and y=x+1
(D) x=z and y-1=x (E) x+y+z=1
D
13. A square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. A square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. V hat is the area of the triangle?

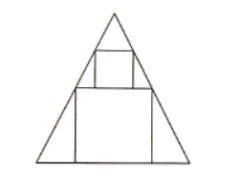
(A) (B) (C) (D) (E)
B
14. Una rolls 6 standard 6-sided dice simultaneously and calculates the product of the 6 numbers obtained. What is the probability that the product is divisible by 4?
(A) (B) (C) (D) (E)
C
15. In square ABCD, point P and Q lie on and , respectively. Segments and intersect at right angles at R, with BR = 6 and PR = 7. What is the area of the square?

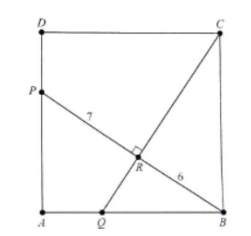
(A) 85 (B) 93 (C) 100 (D) 117 (E) 125
D
16. Five balls are arranged around a circle. Chris chooses two adjacent balls at random and interchanges them. Then Silva does the same, with her choice of adjacent balls to interchange being independent of Chris' s. What is the expected number of balls that occupy their original positions after these two successive transpositions?
(A) 1.6 (B) 1.8 (C) 2.0 (D) 2.2 (E) 2.4
D
17. Distinct lines and m lie in the xy-plane. They intersect at the origin. Point P(-1,4) is reflect about line to the point P’, and then P’ is reflected about line m to point P’’. The equation of line is 5x-y=0, and the coordinates of P’’ are (4,1). What is the equation of line m?
(A) 5x+2y=0 (B) 3x+2y=0 (C) x-3y=0 (D) 2x-3y=0 (E) 5x-3y=0
D
18. Three identical square sheets of paper each with side length 6 are stacked on top of each other. The middle sheet is rotated clockwise 30° about its center and the top sheet is rotated clockwise 60° about its center, resulting in the 24-sided polygon shown in the figure below. The area of this polygon can be expressed in the form , where a, b, and c are positive integers, and c is not divisible by the square of any prime. What is a + b + c?

(A) 75 (B) 93 (C) 96 (D) 129 (E) 147
E
19. Let N be the positive integer 7777…777, a 313-digit number where each digit is a 7. Let f(r) be the leading digit of the rth root of N. What is f(2)+f(3)+f(4)+f(5)+f(6)?
(A) 8 (B) 9 (C) 11 (D) 22 (E) 29
A
20. In a particular game, each of 4 players rolls a standard 6-sided die. The winner is the player who rolls the highest number. If there is a tie for the highest roll, those involved in the tie will roll again and this process will continue until one player wins. Hugo is one of the player in this game. What is the probability that Hugo's first roll was a 5, given that he won the game?
(A) (B) (C) (D) (E)
21. Regular polygons with 5, 6, 7, and 8 sides are inscribed in the same circle. No two of the polygons share a vertex, and no three of their sides intersect at a common point. At how many points inside the circle do two of their sides intersect?
(A) 52 (B) 56 (C) 60 (D) 64 (E) 68
E
22. For each integer , let S_n be the sum of all products jk, where j and k are integers and . What is the sum of the 10 least values of n such that S_n is divisible by 3?
(A) 196 (B) 197 (C) 198 (D) 199 (E) 200
B
23. Each of the 5 sides and the 5 diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability, What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color?
(A) (B) (C) (D) (E) 1
D
24. A cube is constructed from 4 white unit cubes and 4 blue unit cubes. How many different ways are there to construct the cube using these smaller cubes? (Two constructions are considered the same if one can be rotated to match the other.)
(A) 7 (B) 8 (C) 9 (D) 10 (E) 11
A
25. A rectangle with side lengths 1 and 3, a square with side length 1, and a rectangle R are inscribed inside a larger square as shown, The sum of all possible values for the area of R can be written in the form , where m and n are relatively prime positive integers, What is m + n?

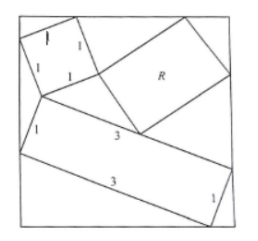
(A) 14 (B) 23 (C) 46 (D) 59 (E) 67
E

2021年11月AMC10B卷考试真题如上所述，可扫码免费领取真题解析

更多年份AMC真题，免费提供

上周结束的2021年AMC10 A试题，已经公布，可以回顾。