紫色彗星数学竞赛真题（2019年初中组）

PURPLE COMET! MATH MEET April 2019
MIDDLE SCHOOL - PROBLEMS
Copyright © Titu Andreescu and Jonathan Kane

Problem 1
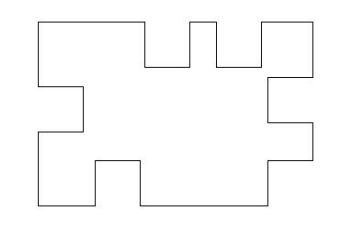
The diagram shows a polygon made by removing six 2 × 2 squares from the sides of an 8 × 12 rectangle. Find the perimeter of this polygon.

Problem 2
Evaluate 1 + 2 − 3 − 4 + 5 + 6 − 7 − 8 + · · · + 2018 − 2019.
Problem 3
The diagram below shows a shaded region bounded by two concentric circles where the outer circle has twice the radius of the inner circle. The total boundary of the shaded region has length 36π. Find n such that the area of the shaded region is nπ.

Problem 4
Of the students attending a school athletic event, 80% of the boys were dressed in the school colors, 60% of the girls were dressed in the school colors, and 45% of the students were girls. Find the percentage of students attending the event who were wearing the school colors.
Problem 5
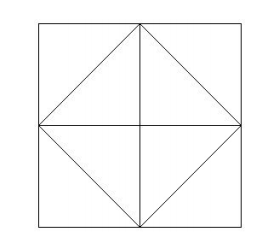
The diagram below shows four congruent squares and some of their diagonals. Let T be the number of triangles and R be the number of rectangles that appear in the diagram. Find T + R.

Problem 6
Find the value of n such that

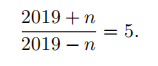
Problem 7
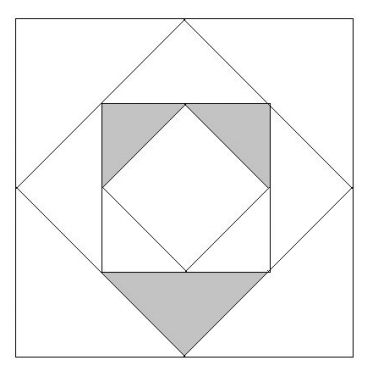
The diagram shows some squares whose sides intersect other squares at the midpoints of their sides. The shaded region has total area 7. Find the area of the largest square.

Problem 8
In the subtraction PURPLE − COMET = MEET each distinct letter represents a distinct decimal digit, and no leading digit is 0. Find the greatest possible number represented by PURPLE.
Problem 9
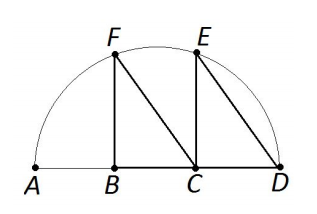
A semicircle has diameter with AD = 30. Points B and C lie on , and points E and F lie on the arc of the semicircle. The two right triangles and are congruent. The area of is m where m and n are positive integers, and n is not divisible by the square of any prime. Find m + n.

Problem 10
Let N be the greatest positive integer that can be expressed using all seven Roman numerals I, V, X, L, C, D, and M exactly once each, and let n be the least positive integer that can be expressed using these numerals exactly once each. Find N − n. Note that the arrangement CM is never used in a number along with the numeral D.
Problem 11
Find the number of positive integers less than or equal to 2019 that are no more than 10 away from a perfect square.
Problem 12
Find the number of ordered triples of positive integers (a, b, c), where a, b, c is a strictly increasing arithmetic progression, a + b + c = 2019, and there is a triangle with side lengths a, b, and c.
Problem 13
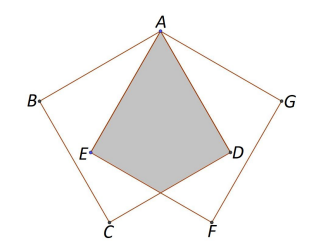
Squares ABCD and AEF G each with side length 12 overlap so that is an equilateral triangle as shown. The area of the region that is in the interior of both squares which is shaded in the diagram is m, where m and n are positive integers, and n is not divisible by the square of any prime. Find m + n.

Problem 14
For real numbers a and b, let f(x) = ax + b and g(x) = x² − x. Suppose that g(f(2)) = 2, g(f(3)) = 0, and g(f(4)) = 6. Find g(f(5)).
Problem 15
Let a, b, c, and d be prime numbers with a ≥ b ≥ c ≥ d > 0. Suppose a² + 2b² + c² + 2d² = 2(ab + bc − cd + da). Find 4a + 3b + 2c + d.
Problem 16
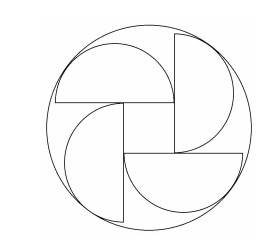
Four congruent semicircular half-disks are arranged inside a circle with radius 4 so that each semicircle is internally tangent to the circle, and the diameters of the semicircles form a 2 × 2 square centered at the center of the circle as shown. The radius of each semicircular half-disk is , where m and n are relatively prime positive integers. Find m + n.

Problem 17
Find the greatest integer n such that 5ⁿ divides 2019! − 2018! + 2017!.
Problem 18
Suppose that a, b, c, and d are real numbers simultaneously satisfying
a + b − c − d = 3
ab − 3bc + cd − 3da = 4
3ab − bc + 3cd − da = 5.
Find 11(a − c)² + 17(b − d)².
Problem 19
Rectangle ABCD has sides AB = 10 and AD = 7. Point G lies in the interior of ABCD a distance 2 from side and a distance 2 from side . Points H, I, J, and K are located on sides , , , and , respectively, so that the path GHIJKG is as short as possible. Then AJ = , where m and n are relatively prime positive integers. Find m + n.
Problem 20
Harold has 3 red checkers and 3 black checkers. Find the number of distinct ways that Harold can place these checkers in stacks. Two ways of stacking checkers are the same if each stack of the first way matches a corresponding stack in the second way in both size and color arrangement. So, for example, the 3 stack arrangement RBR, BR, B is distinct from RBR, RB, B, but the 4 stack arrangement RB, BR, B, R is the same as B, BR, R, RB.

扫码免费领取最新年份学术活动真题及解析