紫色彗星数学竞赛真题（2018年初中组）

PURPLE COMET! MATH MEET April 2018
MIDDLE SCHOOL - PROBLEMS
Copyright © Titu Andreescu and Jonathan Kane

Problem 1
Find n such that the mean of , and is 1.

Problem 2

The following figure is made up of many 2 × 4 tiles such that adjacent tiles always share an edge of length 2. Find the perimeter of this figure.

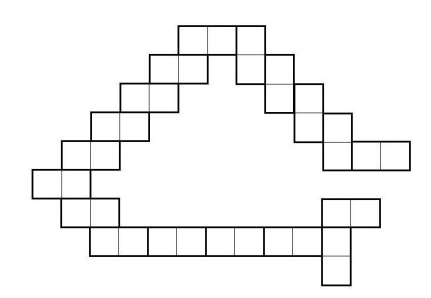
Problem 3
The fraction 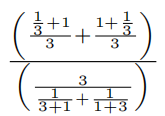can be written as , where m and n are relatively prime positive integers.Find m + n.

Problem 4

The diagram below shows a large square with each of its sides divided into four equal segments. The shaded square whose sides are diagonals drawn to these division points has area 13. Find the area of the large square.

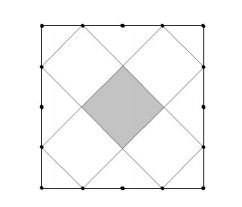
Problem 5

The positive integer m is a multiple of 101, and the positive integer n is a multiple of 63. Their sum is 2018. Find m − n.

Problem 6
Find the greatest integer n such that 10n divides .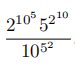

Problem 7
Bradley is driving at a constant speed. When he passes his school, he notices that in 20 minutes he will be exactly  of the way to his destination, and in 45 minutes he will be exactly of the way to his destination. Find the number of minutes it takes Bradley to reach his destination from the point where he passes his school.

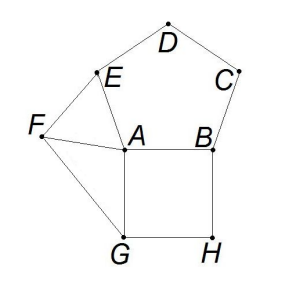
Problem 8
On side of regular pentagon ABCDE there is an equilateral triangle AEF, and on side of the pentagon there is a square ABHG as shown. Find the degree measure of angle AFG.

Problem 9

For some k > 0 the lines 50x + ky = 1240 and ky = 8x + 544 intersect at right angles at the point (m, n). Find m + n.

Problem 10

The triangle below is divided into nine stripes of equal width each parallel to the base of the triangle. The darkened stripes have a total area of 135. Find the total area of the light colored stripes.

Problem 11

Find the number of positive integers less than 2018 that are divisible by 6 but are not divisible by at least one of the numbers 4 or 9.

Problem 12
Line segment has perpendicular bisector , where C is the midpoint of . The segments have lengths AB = 72 and CD = 60. Let R be the set of points P that are midpoints of line segments , where X lies on and Y lies on . Find the area of the region R.

Problem 13

Suppose x and y are nonzero real numbers simultaneously satisfying the equations

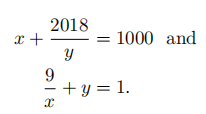
Find the maximum possible value of x + 1000y.

Problem 14

Find the number of ordered quadruples of positive integers (a, b, c, d) such that ab + cd = 10.

Problem 15
There are integers a₁, a₂, a₃, . . . , a₂₄₀ such that x(x + 1)(x + 2)(x + 3)· · ·(x + 239) =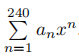. Find the number of integers k with 1 ≤ k ≤ 240 such that a_k is a multiple of 3.

Problem 16
On 4 let D be a point on side , F be a point on side , and E be a point inside the triangle so that || and || . Given that AF = 6, AC = 33, AD = 7, AB = 26, and the area of quadrilateral ADEF is 14, find the area of 4 .

Problem 17

Let a, b, c, and d be real numbers such that a² + b² + c² + d² = 3a + 8b + 24c + 37d = 2018. Evaluate 3b + 8c + 24d + 37a.

Problem 18
Rectangle ABCD has side lengths AB = and BC = . The probability that a randomly chosen point inside the rectangle is closer to the diagonal than to the outside of the rectangle is , where m and n are relatively prime positive integers. Find m + n.

Problem 19

Two identical blue blocks, two identical red blocks, two identical green blocks, and two identical purple blocks are placed next to each other in a row. Find the number of distinct arrangements of these blocks where no blue block is placed next to a red block, and no green block is placed next to a purple block.

Problem 20
Let ABCD be a square with side length 6. Circles X, Y , and Z are congruent circles with centers inside the square such that X is tangent to both sides and , Y is tangent to both sides and , and Z is tangent to side and both circles X and Y . The radius of the circle X can be written m − where m and n are positive integers. Find m + n.