AMC系列 | 第二讲：符合勾股定理的所有整数，都画在坐标系中是什么样？

AMC美国数学学术活动系列将连载12期，根据AMC10/12体系，来讲解其涉及到的各个知识点，并为公立学校和国际学校的学生提供中英文对照。本期要点1.勾股定理的历史2.勾股定理的证明3.勾股定理的应用4.纯代数层面的勾股定理

先来做个小练习：已知一个直角三角形两个斜边长分别是2和3，问斜边长为多少？ok，现在你脑子里一定在想平方、开方的事了。可你有没有想过，为什么要平方和开方。三角形斜边长的平方为什么就是两个直角边的平方和？谁先发现这个有趣性质的？

这就得从勾股定理这个名字讲起，古人把直角三角形较小的直角边叫做勾，较长的直角边叫做股，斜边叫做弦，描述三者关系的定理就叫勾股定理。早在春秋时期，它就被中国人发现，后记载于《九章算数》。

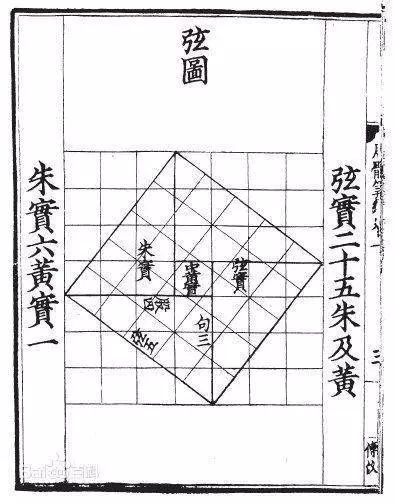
（上图：勾三股四弦五）客观的说，虽然中国人早于西方发现这一性质，但最先将此性质推广到任意直角三角形并予以证明的是古希腊数学家毕达哥拉斯 (Pythagoras) ，因此这个定理也叫做毕达哥拉斯定理 (Pythagorean Theorem) ，我们常见到的黄金分割、整数、分数这些概念也源于毕达哥拉斯学派

这个定理怎么证明呢？中国古人的证法是用割补法，仅用正方形面积公式就能证明：

勾股定理新的证明方法不断被人想出，有趣的是，有个叫加菲尔德的人在用他的方法证出本定理5年之后，成为美国第20任总统，所以人们又称这个证法为“总统证法”。

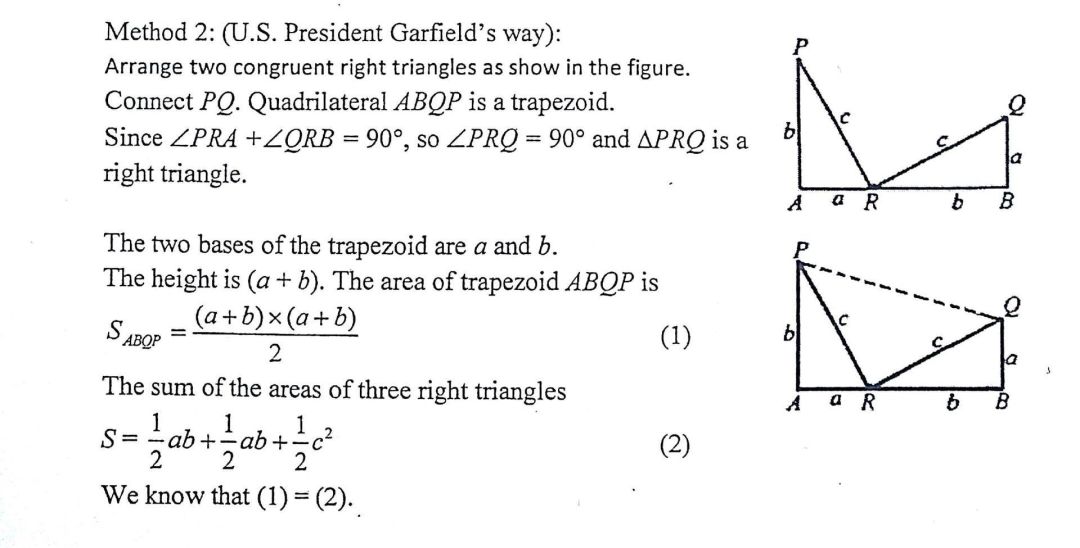
利用梯形面积就是三个三角形面积之和，知道两式相等，然后解出这个式子↓↓

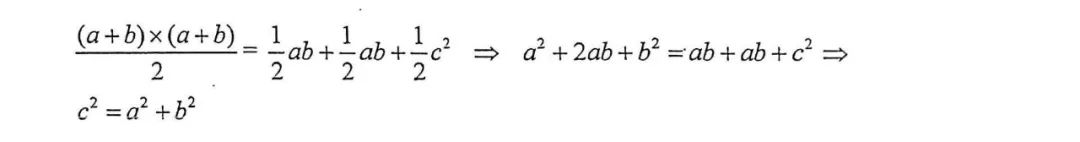
以上两个证法都是基于面积，如果用一些较为现代的数学工具，比如相似三角形 (similar triangles) 那么证明过程就会缩短不少：

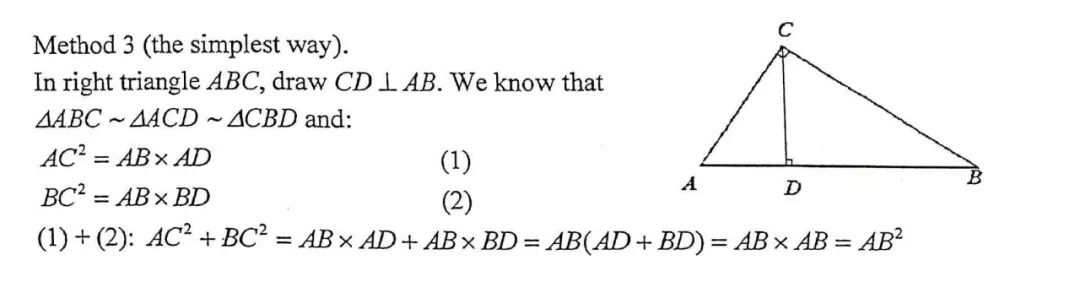
事实上，勾股定理目前有500多种证法，是证明方法最多的数学定理之一。

知道了勾股定理的来源和证明，下面我们来看看它的应用：

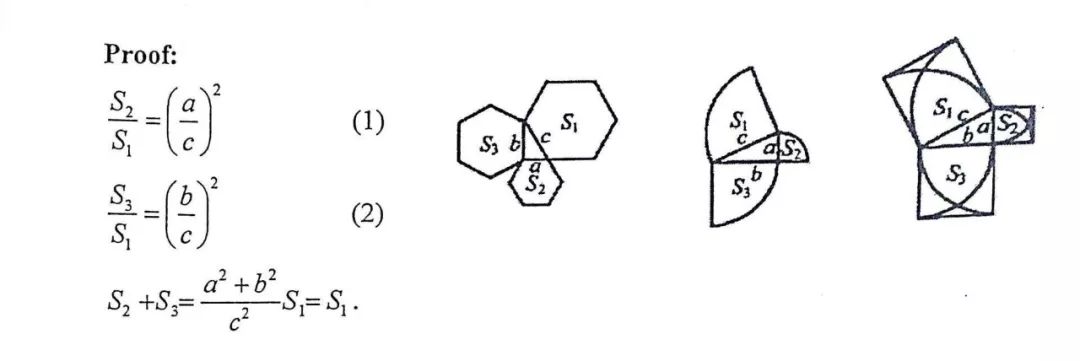
一个重要性质（上图性质1）就是在直角三角形三边上做三个相似的图形，最大的图形面积等于两个小图面积之和（如下图右侧三个例子），证明思路是：相似图形面积比等于边长比的平方，而边长的平方之间的关系就是两个小的加起来等于大的。

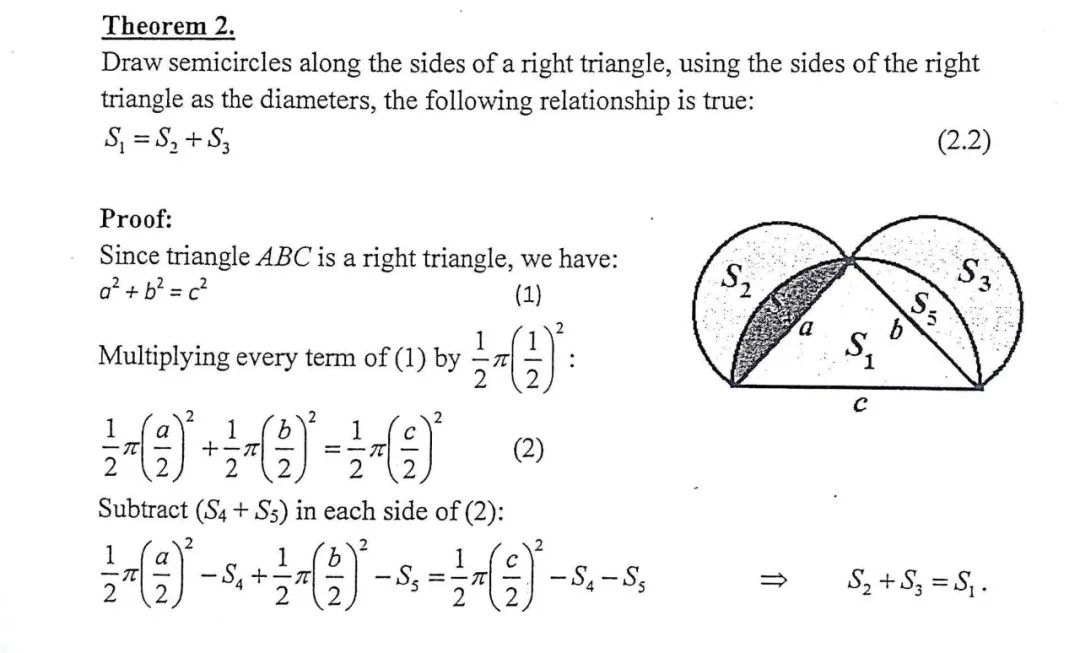
如果做的图形是半圆，结合“直径所对的圆周角是直角”，可推出：以斜边为直径向内做半圆，会经过直角顶点（如下图）。再用面积做差，推出一个新的性质：两个“月牙”面积之和等于三角形面积。

在前面的例子中，我们知道如果一个三角形是直角三角形，那么它的三边 (a,b,c) 就满足 a 方加 b 方等于 c 方，并且在实际题目中，常常出现 （3,4,5）/（6,8,10）/（5,12,13）这样的 (a,b,c) ，这样满足勾股定理的整数，就叫“勾股数”（pythagorean triple) ,勾股数有两个基本性质一：如果一组数是勾股数，那么它们的倍数依然是勾股数。比如 (3,4,5) 是勾股数，那么 (6,8,10) / (9,12,15) / (12,16,20) 以及 (300,400,500) 一定都满足勾股定理，这些勾股数就构成了一类，即 (3k,4k,5k) 。

换个角度讲，如果一组数中三个数可以约分，那么约分到互质 (relatively prime) 后的结果也是勾股数，而且这组勾股数是同类中最小的，这些已经互质的最小的勾股数叫做勾股方程的本原解。

（一部分本原解）二：所有的本原解可以被不重不漏地表示出。其实我们就是就是想知道 “a 方加 b 方等于 c 方”这个方程有哪些互质的 (a,b,c) 解。利用数论知识可以求出，所有互质的解是：

也就是说，有了这个表达式，任意选取两个两个符合条件的 m，n 就能立马“生成”一组勾股数。更直观来看，所有的勾股数，把两直角边的长度作为横纵坐标（下图是实轴坐标和虚轴坐标），就能把所有的勾股数画在图上，每组勾股数的（a，b，c）分别对应横坐标、纵坐标、到原点的距离，这三个量都是整数。

好，今天你学习了《AMC系列》的第二讲，了解了勾股定理的证明，也学会了它的用法和与代数的联系。恭喜你，又解锁了AMC数学学术活动的一个新章节。下次我们将学习学术活动中的相似三角形。