紫色彗星数学竞赛真题（2017年初中组）

PURPLE COMET! MATH MEET April 2017
MIDDLE SCHOOL - PROBLEMS
Copyright © Titu Andreescu and Jonathan Kane

Problem 1
Caden, Zoe, Noah, and Sophia shared a pizza. Caden ate 20 percent of the pizza. Zoe ate 50 percent more of the pizza than Caden ate. Noah ate 50 percent more of the pizza than Zoe ate, and Sophia ate the rest of the pizza. Find the percentage of the pizza that Sophia ate.
Problem 2
The figure below was made by gluing together 5 non-overlapping congruent squares. The figure has area 45. Find the perimeter of the figure.

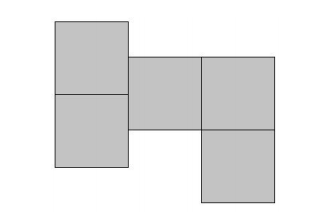
Problem 3
The Stromquist Comet is visible every 61 years. If the comet is visible in 2017, what is the next leap year when the comet will be visible?
Problem 4
The following diagram includes six circles with radius 4, one circle with radius 8, and one circle with radius 16. The area of the shaded region is kπ. Find k.

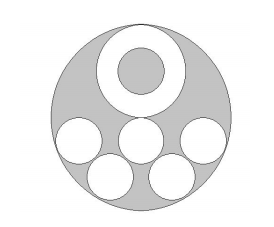
Problem 5
Find the greatest odd divisor of 160³.
Problem 6
On a typical morning Aiden gets out of bed, goes through his morning preparation, rides the bus, and walks from the bus stop to work arriving at work 120 minutes after getting out of bed. One morning Aiden got out of bed late, so he rushed through his morning preparation getting onto the bus in half the usual time, the bus ride took 25 percent longer than usual, and he ran from the bus stop to work in half the usual time it takes him to walk arriving at work 96 minutes after he got out of bed. The next morning Aiden got out of bed extra early, leisurely went through his morning preparation taking 25 percent longer than usual to get onto the bus, his bus ride took 25 percent less time than usual, and he walked slowly from the bus stop to work taking 25 percent longer than usual. How many minutes after Aiden got out of bed did he arrive at work that day?
Problem 7
Find the number of positive integers less than 100 that are divisors of 300.
Problem 8
The positive integer m is a multiple of 111, and the positive integer n is a multiple of 31. Their sum is 2017. Find n − m.
Problem 9

Problem 10
Find the number of rearrangements of the letters in the word MATHMEET that begin and end with the same letter such as TAMEMHET.
Problem 11
Find the greatest prime divisor of 29! + 33!.
Problem 12
Let x, y, and z be real numbers such that
12x − 9y² = 7
6y − 9z² = −2
12z − 9x² = 4.
Find 6x² + 9y² + 12z².
Problem 13
Find the number of positive integer divisors of 20¹⁷ that are either perfect squares or perfect cubes.
Problem 14
Let a and b be positive integers such that a + ab = 1443 and ab + b = 1444. Find 10a + b.
Problem 15
Find the remainder when is divided by 1000.
Problem 16
The set of positive real numbers x that satisfy 2 |x² − 9| ≤ 9|x| is an interval [m, M]. Find 10m + M.
Problem 17
Let a₀, a₁, ..., a₆ be real numbers such that a₀ + a₁ + ... + a₆ = 1 and
a₀ + a₂ + a₃ + a₄ + a₅ + a₆ =
a₀ + a₁ + a₃ + a₄ + a₅ + a₆ =
a₀ + a₁ + a₂ + a₄ + a₅ + a₆ =
a₀ + a₁ + a₂ + a₃ + a₅ + a₆ =
a₀ + a₁ + a₂ + a₃ + a₄ + a₆ =
a₀ + a₁ + a₂ + a₃ + a₄ + a₅ =
The value of a₀ is , where m and n are relatively prime positive integers. Find m + n.
Problem 18
Omar has four fair standard six-sided dice. Omar invented a game where he rolls his four dice over and over again until the number 1 does not appear on the top face of any of the dice. Omar wins the game if on that roll the top faces of his dice show at least one 2 and at least one 5. The probability that Omar wins the game is , where m and n are relatively prime positive integers. Find m + n.
Problem 19
Find the sum of all values of a + b, where (a, b) is an ordered pair of positive integers and a2 + is a perfect square.
Problem 20
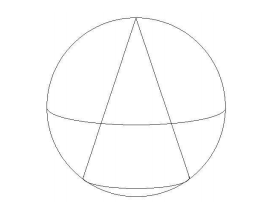
A right circular cone has a height equal to three times its base radius and has volume 1. The cone is inscribed inside a sphere as shown. The volume of the sphere is , where m and n are relatively prime positive integers. Find m + n.

扫码免费领取最新年份学术活动真题及解析