- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
紫色彗星数学竞赛真题(2018年高中组)
PURPLE COMET! MATH MEET April 2018
HIGH SCHOOL - PROBLEMS
Copyright Titu Andreescu and Jonathan Kane
Problem 1
Find the positive integer n such that 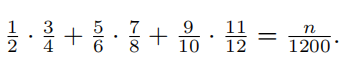
Problem 2
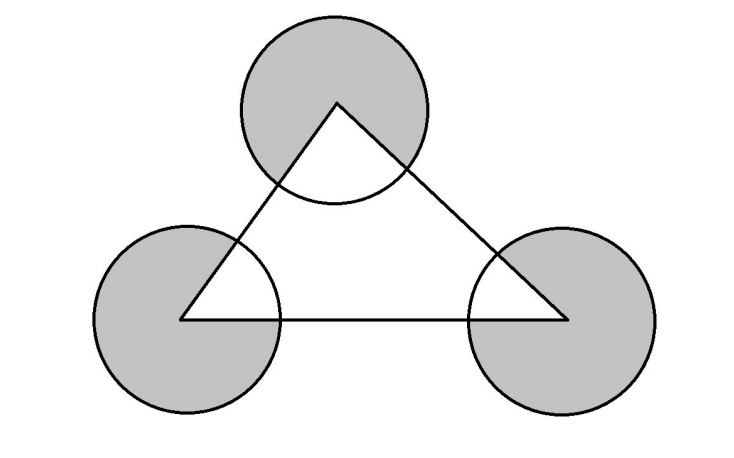
A triangle with side lengths 16, 18, and 21 has a circle with radius 6 centered at each vertex. Find n so that the total area inside the three circles but outside of the triangle is nπ.
Problem 3
Find x so that the arithmetic mean of x, 3x, 1000, and 3000 is 2018.
Problem 4
The following diagram shows a grid of 36 cells. Find the number of rectangles pictured in the diagram that contain at least three cells of the grid.

Problem 5
One afternoon at the park there were twice as many dogs as there were people, and there were twice as many people as there were snakes. The sum of the number of eyes plus the number of legs on all of these dogs, people, and snakes was 510. Find the number of dogs that were at the park.
Problem 6
Triangle ABC has AB = AC. Point D is on side ![]() so that AD = CD and ∠BAD = 36° . Find the degree measure of ∠BAC.
so that AD = CD and ∠BAD = 36° . Find the degree measure of ∠BAC.
Problem 7
In 10 years the product of Melanie’s age and Phil’s age will be 400 more than it is now. Find what the sum of Melanie’s age and Phil’s age will be 6 years from now.
Problem 8
Let a and b be positive integers such that 2a − 9b + 18ab = 2018. Find b − a.
Problem 9
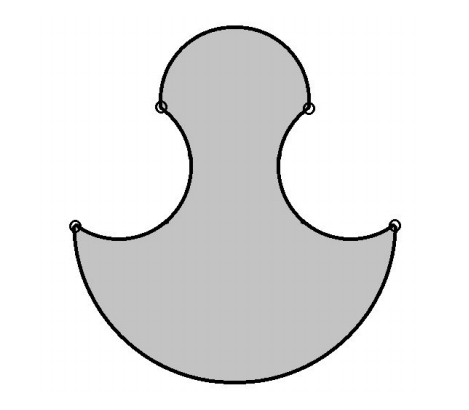
A trapezoid has side lengths 10, 10, 10, and 22. Each side of the trapezoid is the diameter of a semicircle with the two semicircles on the two parallel sides of the trapezoid facing outside the trapezoid and the other two semicircles facing inside the trapezoid as shown. The region bounded by these four semicircles has area m + nπ, where m and n are positive integers. Find m + n.
Problem 10
Find the remainder when 112018 is divided by 100.
Problem 11
Find the number of positive integers k ≤ 2018 for which there exist integers m and n so that k = 2m + 2n. For example, 64 = 25 + 25 , 65 = 20 + 26 , and 66 = 21 + 26.
Problem 12
A jeweler can get an alloy that is 40% gold for 200 dollars per ounce, an alloy that is 60% gold for 300 dollar per ounce, and an alloy that is 90% gold for 400 dollars per ounce. The jeweler will purchase some of these gold alloy products, melt them down, and combine them to get an alloy that is 50% gold. Find the minimum number of dollars the jeweler will need to spend for each ounce of the alloy she makes.
Problem 13
Five lighthouses are located, in order, at points A, B, C, D, and E along the shore of a circular lake with a diameter of 10 miles. Segments ![]() are diameters of the circle. At night, when sitting at A, the lights from B, C, D, and E appear to be equally spaced along the horizon. The perimeter in miles of pentagon ABCDE can be written
are diameters of the circle. At night, when sitting at A, the lights from B, C, D, and E appear to be equally spaced along the horizon. The perimeter in miles of pentagon ABCDE can be written ![]() , where m and n are positive integers. Find m + n.
, where m and n are positive integers. Find m + n.
Problem 14
A complex number z whose real and imaginary parts are integers satisfifies ![]() (2018)(81), where Re(w) and Im(w) are the real and imaginary parts of w, respectively. Find
(2018)(81), where Re(w) and Im(w) are the real and imaginary parts of w, respectively. Find ![]()
Problem 15
Let a and b be real numbers such that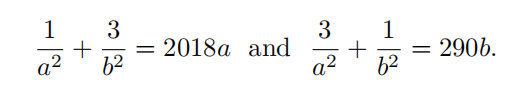
Then ![]() , where m and n are relatively prime positive integers. Find m + n.
, where m and n are relatively prime positive integers. Find m + n.
Problem 16
If you roll four standard, fair six-sided dice, the top faces of the dice can show just one value (for example, 3333), two values (for example, 2666), three values (for example, 5215), or four values (for example, 4236). The mean number of values that show is ![]() , where m and n are relatively prime positive integers.
, where m and n are relatively prime positive integers.
Find m + n.
Problem 17
One afternoon a bakery fifinds that it has 300 cups of flflour and 300 cups of sugar on hand. Annie and Sam decide to use this to make and sell some batches of cookies and some cakes. Each batch of cookies will require 1 cup of flflour and 3 cups of sugar. Each cake will require 2 cups of flflour and 1 cup of sugar. Annie thinks that each batch of cookies should sell for 2 dollars and each cake for 1 dollar, but Sam thinks that each batch of cookies should sell for 1 dollar and each cake should sell for 3 dollars. Find the difffference between the maximum dollars of income they can receive if they use Sam’s selling plan and the maximum dollars of income they can receive if they use Annie’s selling plan.
Problem 18
Find the positive integer k such that the roots of x3 − 15x2 + kx − 1105 are three distinct collinear points in the complex plane.
Problem 19
Suppose that a and b are positive real numbers such that ![]() Find
Find ![]()
Problem 20
Aileen plays badminton where she and her opponent stand on opposite sides of a net and attempt to bat a birdie back and forth over the net. A player wins a point if their opponent fails to bat the birdie over the net. When Aileen is the server (the fifirst player to try to hit the birdie over the net), she wins a point with probability ![]() . Each time Aileen successfully bats the birdie over the net, her opponent, independent of all
. Each time Aileen successfully bats the birdie over the net, her opponent, independent of all
previous hits, returns the birdie with probability ![]() Each time Aileen bats the birdie, independent of all previous hits, she returns the birdie with probability
Each time Aileen bats the birdie, independent of all previous hits, she returns the birdie with probability ![]() , where m and n are relatively prime positive integers. Find m + n.
, where m and n are relatively prime positive integers. Find m + n.
Problem 21
Let x be in the interval ![]() such that sin x − cos x =
such that sin x − cos x = ![]() Then sin3 x + cos3 x =
Then sin3 x + cos3 x = 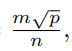 where m, n, and p are relatively prime positive integers, and p is not divisible by the square of any prime. Find m + n + p.
where m, n, and p are relatively prime positive integers, and p is not divisible by the square of any prime. Find m + n + p.
Problem 22
Positive integers a and b satisfy a3 + 32b + 2c = 2018 and b3 + 32a + 2c = 1115. Find a2 + b2 + c2.
Problem 23
Let a, b, and c be integers simultaneously satisfying the equations 4abc + a + b + c = 2018 and ab + bc + ca = −507. Find |a| + |b| + |c|.
Problem 24
Five girls and five boys randomly sit in ten seats that are equally spaced around a circle. The probability that there is at least one diameter of the circle with two girls sitting on opposite ends of the diameter is ![]() , where m and n are relatively prime positive integers. Find m + n.
, where m and n are relatively prime positive integers. Find m + n.
Problem 25
If a and b are in the interval ![]() such that 13(sin a + sin b) + 43(cos a + cos b) =
such that 13(sin a + sin b) + 43(cos a + cos b) = ![]() then tan a + tan b =
then tan a + tan b = ![]() , where m and n are relatively prime positive integers. Find m + n.
, where m and n are relatively prime positive integers. Find m + n.
Problem 26
Let a, b, and c be real numbers. Let u = a2 + b2 + c2 and v = 2ab + 2bc + 2ca. Suppose 2018u = 1001v + 1024. Find the maximum possible value of 35a − 28b − 3c.
Problem 27
Suppose p < q < r < s are prime numbers such that pqrs + 1 = 4p+q . Find r + s.
Problem 28
In △ABC points D, E, and F lie on side ![]() such that
such that ![]() is an angle bisector of ∠BAC,
is an angle bisector of ∠BAC,![]() is a median, and
is a median, and ![]() is an altitude. Given that AB = 154 and AC = 128, and 9 · DE = EF, fifind the side length BC.
is an altitude. Given that AB = 154 and AC = 128, and 9 · DE = EF, fifind the side length BC.
Problem 29
Find the three-digit positive integer n for which 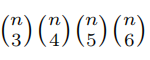 is a perfect square.
is a perfect square.
Problem 30
One right pyramid has a base that is a regular hexagon with side length 1, and the height of the pyramid is 8. Two other right pyramids have bases that are regular hexagons with side length 4, and the heights of those pyramids are both 7. The three pyramids sit on a plane so that their bases are adjacent to each other and meet at a single common vertex. A sphere with radius 4 rests above the plane supported by these three pyramids. The distance that the center of the sphere is from the plane can be written as ![]() , where p, q, and r are relatively prime positive integers, and q is not divisible by the square of any prime. Find p + q + r.
, where p, q, and r are relatively prime positive integers, and q is not divisible by the square of any prime. Find p + q + r.
扫描下方二维码获取本年度学术活动答案及解析
还可免费领取最新年度真题及答案解析


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









