紫色彗星数学竞赛真题（2015年初中组）

PURPLE COMET! MATH MEET April 2015
MIDDLE SCHOOL - PROBLEMS
Copyright © Titu Andreescu and Jonathan Kane

Problem 1
Arvin ate 11 halves of tarts, Bernice ate 12 quarters of tarts, Chrisandra ate 13 eighths of tarts, and Drake ate 14 sixteenths of tarts. How many tarts were eaten?
Problem 2
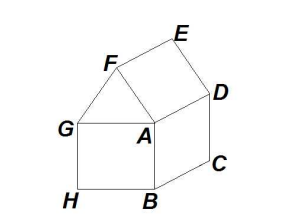
The diagram below is made up of a rectangle AGHB, an equilateral triangle AF G, a rectangle ADEF,and a parallelogram ABCD. Find the degree measure of

Problem 3
The repeating decimal 2.0151515 . . . can be expressed as , where m and n are relatively prime positive integers. Find m + n.
Problem 4
Janet played a song on her clarinet in 3 minutes and 20 seconds. Janet’s goal is to play the song at a 25% faster rate. Find the number of seconds it will take Janet to play the song when she reaches her goal.
Problem 5
The diagram below shows a rectangle with one side divided into seven equal segments and the opposite side divided in half. The rectangle has area 350. Find the area of the shaded region.

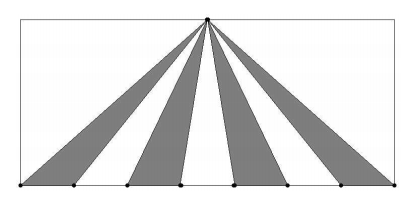
Problem 6
Find the least positive integer whose digits add to a multiple of 27 yet the number itself is not a multiple of 27. For example, 87999921 is one such number.
Problem 7
How many non-congruent isosceles triangles (including equilateral triangles) have positive integer side lengths and perimeter less than 20?
Problem 8
Gwendoline rolls a pair of six-sided dice and records the product of the two values rolled. Gwendoline repeatedly rolls the two dice and records the product of the two values until one of the values she records appears for a third time. What is the maximum number of times Gwendoline will need to roll the two dice?
Problem 9
The figure below has only two sizes for its internal angles. The larger angles are three times the size of the smaller angles. Find the degree measure of one of the larger angles.

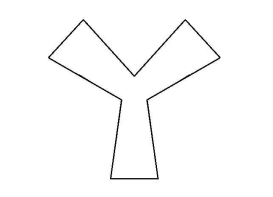
Problem 10
In an abandoned chemistry lab Gerome found a two-pan balance scale and three 1-gram weights, three 5-gram weights, and three 50-gram weights. By placing one pile of chemicals and as many weights as necessary on the pans of the scale, Gerome can measure out various amounts of the chemicals in the pile. Find the number of different positive weights of chemicals that Gerome could measure.

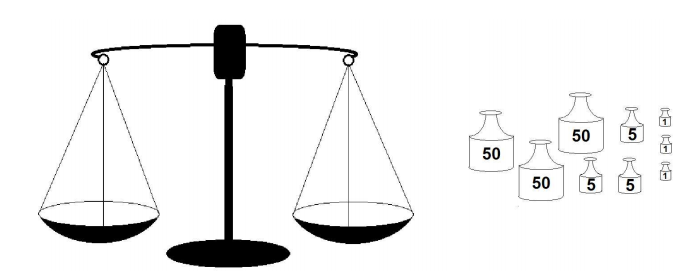
Problem 11
The Purple Plant Garden Store sells grass seed in ten-pound bags and fifteen-pound bags. Yesterday half of the grass seed they had was in ten-pound bags. This morning the store received a shipment of 27 more ten-pound bags, and now they have twice as many ten-pound bags as fifteen-pound bags. Find the total weight in pounds of grass seed the store now has.
Problem 12

Problem 13
Given that x, y, and z are real numbers satisfying x + y + z = 10 and x² + y² + z² = 50, find the maximum possible value of (x + 2y + 3z)² + (y + 2z + 3x)² + (z + 2x + 3y)².
Problem 14
Find the greatest positive integer n so that 3ⁿ divides 70! + 71! + 72!.
Problem 15
How many positive integers less than 2015 have exactly 9 positive integer divisors?
Problem 16
Jamie, Linda, and Don bought bundles of roses at a flower shop, each paying the same price for each bundle. Then Jamie, Linda, and Don took their bundles of roses to a fair where they tried selling their bundles for a fixed price which was higher than the price that the flower shop charged. At the end of the fair, Jamie, Linda, and Don donated their unsold bundles of roses to the fair organizers. Jamie had bought 20 bundles of roses, sold 15 bundles of roses, and made $60 profit. Linda had bought 34 bundles of roses, sold 24 bundles of roses, and made $69 profit. Don had bought 40 bundles of roses and sold 36 bundles of roses. How many dollars profit did Don make?
Problem 17

Problem 18
You have many identical cube-shaped wooden blocks. You have four colors of paint to use, and you paint each face of each block a solid color so that each block has at least one face painted with each of the four colors. Find the number of distinguishable ways you could paint the blocks. (Two blocks are distinguishable if you cannot rotate one block so that it looks identical to the other block.)
Problem 19
Let a, b, c, and d be real numbers such that

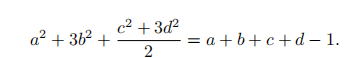
Find 1000a + 100b + 10c + d.
Problem 20
The diagram below shows an 8 × 7 rectangle with a 3−4−5 right triangle drawn in each corner. The lower two triangles have their sides of length 4 along the bottom edge of the rectangle, while the upper two triangles have their sides of length 3 along the top edge of the rectangle. A circle is tangent to the hypotenuse of each triangle. The diameter of the circle is , where m and n are relatively prime positive integers. Find m + n.

扫码免费领取最新年份学术活动真题及解析