紫色彗星数学竞赛真题（2013年初中组）

PURPLE COMET! MATH MEET April 2013
MIDDLE SCHOOL - PROBLEMS
Copyright ©Titu Andreescu and Jonathan Kane

Problem 1
The diagram shows two congruent isosceles triangles in a 20 × 20 square which has been partitioned into four 10 × 10 squares. Find the area of the shaded region.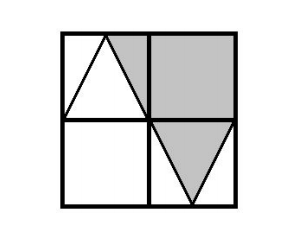

Problem 2
Floyd looked at a standard 12 hour analogue clock at 2:36. When Floyd next looked at the clock, the angles through which the hour hand and the minute hand of the clock had moved added to 247 degrees. How many minutes after 3:00 was that?
Problem 3
Let N be the sum of the first four three-digit prime numbers. Find the sum of the prime factors of .
Problem 4
One of the two Purple Comet! question writers is an adult whose age is the same as the last two digits of the year he was born. His birthday is in August. What is his age today?
Problem 5
A picture with an area of 160 square inches is surrounded by a 2 inch border. The picture with its border is a rectangle twice as long as it is wide. How many inches long is that rectangle?
Problem 6
Pete’s research shows that the number of nuts collected by the squirrels in any park is proportional to the square of the number of squirrels in that park. If Pete notes that four squirrels in a park collect 60 nuts, how many nuts are collected by 20 squirrels in a park?
Problem 7
How many seven-digit positive integers do not either start or end with 7?
Problem 8
Asheville, Bakersfield, Charter, and Darlington are four small towns along a straight road in that order. The distance from Bakersfield to Charter is one-third the distance from Asheville to Charter and one-quarter the distance from Bakersfield to Darlington. If it is 12 miles from Bakersfield to Charter, how many miles is it from Asheville to Darlington?
Problem 9
Find the sum of all four-digit integers whose digits are a rearrangement of the digits 1, 2, 3, 4, such as 1234, 1432, or 3124.
Problem 10
Find the least positive integer k so that the mean of the numbers k, k + 1, k + 2, k + 3, . . . , 2k exceeds 200.
Problem 11
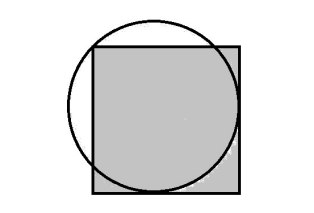
In the following diagram two sides of a square are tangent to a circle with diameter 8. One corner of the square lies on the circle. There are positive integers m and n so that the area of the square is m + √n. Find m + n.

Problem 12
Find integer n such that both n − 86 and n + 86 are perfect squares.
Problem 13

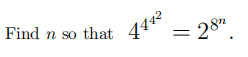
Problem 14
How many triangles appear in the diagram below?

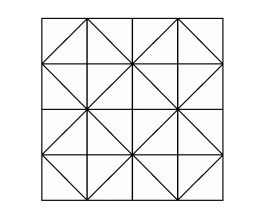
Problem 15
Let a, b, and c be positive real numbers such that a² + b² + c² = 989 and (a + b)² + (b + c)² + (c + a)² = 2013. Find a + b + c.
Problem 16
A quarry wants to sell a large pile of gravel. At full price, the gravel would sell for 3200 dollars. But during the first week the quarry only sells 60% of the gravel at full price. The following week the quarry drops the price by 10%, and, again, it sells 60% of the remaining gravel. Each week, thereafter, the quarry reduces the price by another 10% and sells 60% of the remaining gravel. This continues until there is only a handful of gravel left. How many dollars does the quarry collect for the sale of all its gravel?
Problem 17
A rectangle has side lengths 6 and 8. There are relatively prime positive integers m and n so that is the probability that a point randomly selected from the inside of the rectangle is closer to a side of the rectangle than to either diagonal of the rectangle. Find m + n.
Problem 18
Six children stand in a line outside their classroom. When they enter the classroom, they sit in a circle in random order. There are relatively prime positive integers m and n so that is the probability that no two children who stood next to each other in the line end up sitting next to each other in the circle. Find m + n.
Problem 19
For positive integer n let an be the integer consisting of n digits of 9 followed by the digits 488. For example, a3 = 999,488 and a7 = 9,999,999,488. Find the value of n so that a_n is divisible by the highest power of 2.
Problem 20
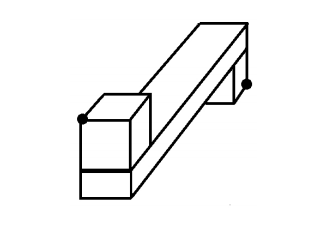
The diagram below shows a 1 × 2 × 10 duct with 2 × 2 × 2 cubes attached to each end. The resulting object is empty, but the entire surface is solid sheet metal. A spider walks along the inside of the duct between the two marked corners. There are positive integers m and n so that the shortest path the spider could take has length √m + √n. Find m + n.

扫码免费领取最新年份学术活动真题及解析