Home » 国际竞赛 » Details

紫色彗星数学竞赛真题（2016年高中组）

Category: 国际竞赛, 数学国际竞赛 Date: 2021年11月16日下午5:08

PURPLE COMET! MATH MEET April 2016

HIGH SCHOOL - PROBLEMS

Problem 1

Two integers have a sum of 2016 and a difffference of 500. Find the larger of the two integers.

Problem 2

The trapezoid below has bases with lengths 7 and 17 and area 120. Find the difffference of the areas of the two triangles.

Problem 3

Find the positive integer n such that 10n cubic centimeters is the same as 1 cubic kilometer.

Problem 4

One side of a rectangle has length 18. The area plus the perimeter of the rectangle is 2016. Find the perimeter of the rectangle.

Problem 5

Julius has a set of fifive positive integers whose mean is 100. If Julius removes the median of the set of fifive numbers, the mean of the set increases by 5, and the median of the set decreases by 5. Find the maximum possible value of the largest of the fifive numbers Julius has.

Problem 6

The following diagram shows a square where each side has seven dots that divide the side into six equal segments. All the line segments that connect these dots that form a 45° angle with a side of the square are drawn as shown. The area of the shaded region is 75. Find the area of the original square.

Problem 7

Positive integers m and n are both greater than 50, have a least common multiple equal to 480, and have a

greatest common divisor equal to 12. Find m + n.

Problem 8

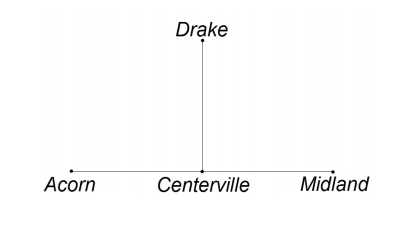
The map below shows an east/west road connecting the towns of Acorn, Centerville, and Midland, and a north/south road from Centerville to Drake. The distances from Acorn to Centerville, from Centerville to Midland, and from Centerville to Drake are each 60 kilometers. At noon Aaron starts at Acorn and bicycles east at 17 kilometers per hour, Michael starts at Midland and bicycles west at 7 kilometers per hour, and David starts at Drake and bicycles at a constant rate in a straight line across an open fifield. All three bicyclists arrive at exactly the same time at a point along the road from Centerville to Midland. Find the number of kilometers that David bicycles.

Problem 9

Find the sum of all perfect squares that divide 2016.

Problem 10

Jeremy wrote all the three-digit integers from 100 to 999 on a blackboard. Then Allison erased each of the 2700 digits Jeremy wrote and replaced each digit with the square of that digit. Thus, Allison replaced every 1 with a 1, every 2 with a 4, every 3 with a 9, every 4 with a 16, and so forth. The proportion of all the digits Allison wrote that were ones is , where m and n are relatively prime positive integers. Find m + n.

Problem 11

Find the number of three-digit positive integers which have three distinct digits where the sum of the digits

is an even number such as 925 and 824.

Problem 12

Find the number whose reciprocal is the sum of the reciprocal of 9 + 15i and the reciprocal of 9 − 15i.

Problem 13

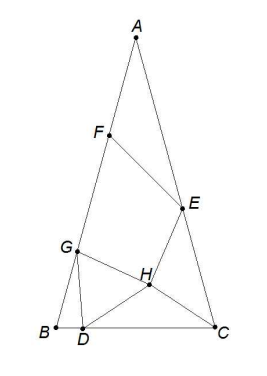
In 4 ABC shown below, AB = AC, AF = EF, and EH = CH = DH = GH = DG = BG. Also, ∠CHE = ∠F GH. Find the degree measure of ∠BAC.

Problem 14

Find the greatest possible value of pq + r, where p, q, and r are (not necessarily distinct) prime numbers satisfying pq + qr + rp = 2016.

Problem 15

Find the least positive integer of the form where a and b are distinct digits, such that the integer can be written as a product of six distinct primes.

Problem 16

Henry rolls a fair die. If the die shows the number k, Henry will then roll the die k more times. The probability that Henry will never roll a 3 or a 6 either on his fifirst roll or on one of the k subsequent rolls is given by , where m and n are relatively prime positive integers. Find m + n.

Problem 17

The cubic polynomials p(x) and q(x) satisfy

p(1) = q(2)
p(3) = q(4)
p(5) = q(6)
p(7) = q(8) + 13.

Find p(9) − q(10).

Problem 18

The Tasty Candy Company always puts the same number of pieces of candy into each one-pound bag of candy they sell. Mike bought 4 one-pound bags and gave each person in his class 15 pieces of candy. Mike had 23 pieces of candy left over. Betsy bought 5 one-pound bags and gave 23 pieces of candy to each teacher in her school. Betsy had 15 pieces of candy left over. Find the least number of pieces of candy the Tasty Candy Company could have placed in each one-pound bag.

Problem 19

Jar #1 contains fifive red marbles, three blue marbles, and one green marble.

Jar #2 contains fifive blue marbles, three green marbles, and one red marble.

Jar #3 contains fifive green marbles, three red marbles, and one blue marble.

You randomly select one marble from each jar. Given that you select one marble of each color, the probability that the red marble came from jar #1, the blue marble came from jar #2, and the green marble came from jar #3 can be expressed as , where m and n are relatively prime positive integers. Find m + n.

Problem 20

Positive integers a, b, c, d, and e satisfy the equations

(a + 1)(3bc + 1) = d + 3e + 1

(b + 1)(3ca + 1) = 3d + e + 13

(c + 1)(3ab + 1) = 4(26 − d − e) − 1.

Find d² + e².

Problem 21

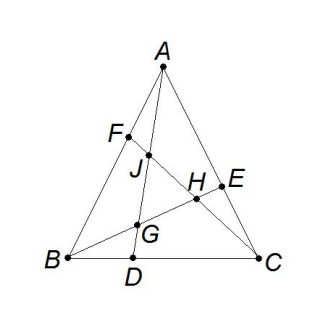
On equilateral 4 ABC point D lies on a distance 1 from B, point E lies on a distance 1 from C, and point F lies on AB a distance 1 from A. Segments and intersect in pairs at points G, H, and J which are the vertices of another equilateral triangle. The area of △ABC is twice the area of △GHJ. The side length of △ABC can be written where r, s, and t are relatively prime positive integers. Find r + s + t.

Problem 22

In △ABC, cos ∠A =, cos ∠B =, and BC = 24. Find the length AC.

Problem 23

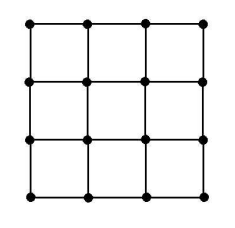
Sixteen dots are arranged in a four by four grid as shown. The distance between any two dots in the grid is the minimum number of horizontal and vertical steps along the grid lines it takes to get from one dot to the other. For example, two adjacent dots are a distance 1 apart, and two dots at opposite corners of the grid are a distance 6 apart. The mean distance between two distinct dots in the grid is , where m and n

are relatively prime positive integers. Find m + n.

Problem 24

Find the largest prime p such that p divides 2^p+1 + 3^p+1 + 5^p+1 + 7^p+1 .

Problem 25

For n measured in degrees let T(n) = cos² (30° − n) − cos(30°− n) cos(30°+ n) + cos² (30°+ n). Evaluate

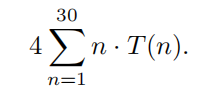
Problem 26

Find the sum of all values of a such that there are positive integers a and b satisfying = 2016.

Problem 27

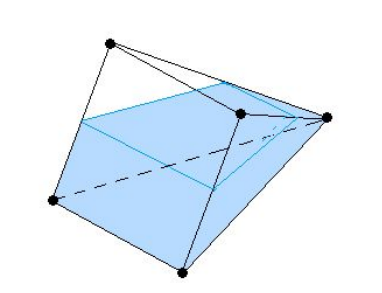
A container the shape of a pyramid has a 12 × 12 square base, and the other four edges each have length 11 The container is partially fifilled with liquid so that when one of its triangular faces is lying on a flflat surface, the level of the liquid is half the distance from the surface to the top edge of the container. Find the volume of the liquid in the container.

Problem 28

Find the sum of all the possible values of xy such that x and y are positive integers satisfying

(x² + 1)(y² + 1) + 2(x − y)(1 − xy) = 4(1 + xy) + 140.

Problem 29

Ten square tiles are placed in a row, and each can be painted with one of the four colors red (R), yellow (Y), blue (B), and white (W). Find the number of ways this can be done so that each block of fifive adjacent tiles contains at least one tile of each color. That is, count the patterns RWBWYRRBWY and WWBYRWYBWR but not RWBYYBWWRY because the fifive adjacent tiles colored BYYBW does not include the color red.

Problem 30

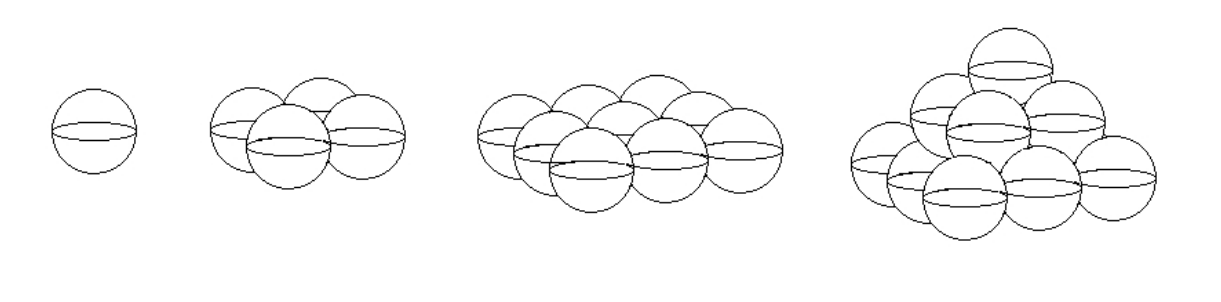
Some identically sized spheres are piled in n layers in the shape of a square pyramid with one sphere in the top layer, 4 spheres in the second layer, 9 spheres in the third layer, and so forth so that the bottom layer has a square array of n2 spheres. In each layer the centers of the spheres form a square grid so that each sphere is tangent to any sphere adjacent to it on the grid. Each sphere in an upper level is tangent to the four spheres directly below it. The diagram shows how the fifirst three layers of spheres are stacked. A square pyramid is built around the pile of spheres so that the sides of the pyramid are tangent to the spheres on the outside of the pile. There is a positive integer m such that as n gets large, the ratio of the volume of the pyramid to the total volume inside all of the spheres approaches Find m.