Home » 国际竞赛 » Details

紫色彗星数学竞赛真题（2015年高中组）

Category: 国际竞赛, 数学国际竞赛 Date: 2021年11月15日下午6:48

PURPLE COMET! MATH MEET April 2015

HIGH SCHOOL - PROBLEMS

Problem 1

The fifive numbers 17, 98, 39, 54, and n have a mean equal to n. Find n.

Problem 2

How many sets of two positive prime numbers {p, q} have the property that p + q = 100?

Problem 3

The Fahrenheit temperature (F) is related to the Celsius temperature (C) by F = · C + 32. What is the temperature in Fahrenheit degrees that is one-fififth as large if measured in Celsius degrees?

Problem 4

Six boxes are numbered 1, 2, 3, 4, 5, and 6. Suppose that there are N balls distributed among these six boxes. Find the least N for which it is guaranteed that for at least one k, box number k contains at least k² balls.

Problem 5

The two diagonals of a quadrilateral have lengths 12 and 9, and the two diagonals are perpendicular to each other. Find the area of the quadrilateral.

Problem 6

There are digits a and b so that the 15-digit number is divisible by 99. Find 10a + b.

Problem 7

Talya went for a 6 kilometer run. She ran 2 kilometers at 12 kilometers per hour followed by 2 kilometers at 10 kilometers per hour followed by 2 kilometers at 8 kilometers per hour. Talya’s average speed for the 6 kilometer run was kilometers per hour, where m and n are relatively prime positive integers.

Find m + n.

Problem 8

In the fifigure below ∠LAM = ∠LBM = ∠LCM = ∠LDM, and ∠AEB = ∠BF C = ∠CGD = 34◦ . Given that ∠KLM = ∠KML, fifind the degree measure of ∠AEF.

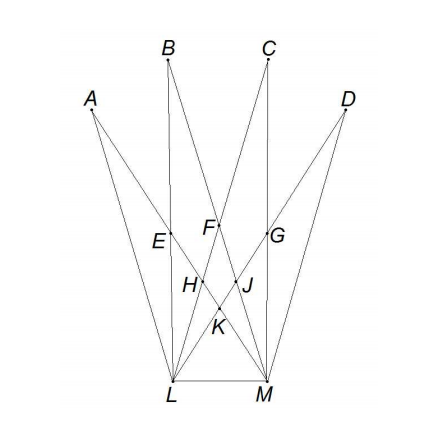
Problem 9

Find the sum of all positive integers n with the property that the digits of n add up to 2015 − n.

Problem 10

Find the sum of all the real values of x satisfying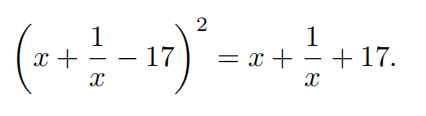

Problem 11

Suppose that the vertices of a polygon all lie on a rectangular lattice of points where adjacent points on the lattice are a distance 1 apart. Then the area of the polygon can be found using Pick’s Formula: I + − 1, where I is the number of lattice points inside the polygon, and B is the number of lattice points on the boundary of the polygon. Pat applied Pick’s Formula to fifind the area of a polygon but mistakenly interchanged the values of I and B. As a result, Pat’s calculation of the area was too small by 35. Using the correct values for I and B, the ratio n = is an integer. Find the greatest possible value of n.

Problem 12

The product 20! · 21! · 22! · · · 28! can be expressed in the form m · n³ , where m and n are positive integers, and m is not divisible by the cube of any prime. Find m.

Problem 13

The diagram below shows a parallelogram ABCD with AB = 36 and AD = 60. Diagonal is perpendicular to side . Points E and F bisect sides and , respectively. Points G and H are the intersections of with and , respectively. Find the area of quadrilateral EGFH.

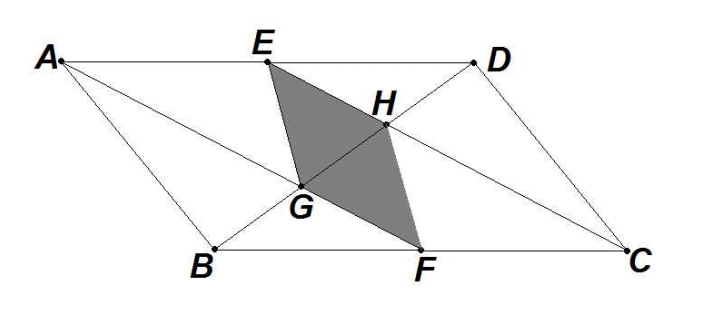
Problem 14

Evaluate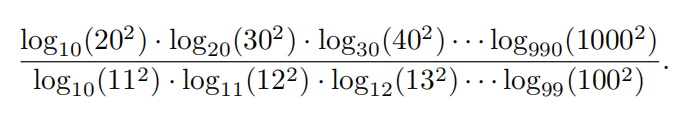

Problem 15

On the inside of a square with side length 60, construct four congruent isosceles triangles each with base 60 and height 50, and each having one side coinciding with a difffferent side of the square. Find the area of the octagonal region common to the interiors of all four triangles.

Problem 16

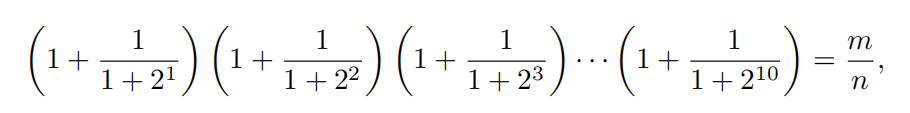
where m and n are relatively prime positive integers. Find m + n.

Problem 17

How many subsets of {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} have the property that no two of its elements diffffer by more than 5? For example, count the sets {3}, {2, 5, 7}, and {5, 6, 7, 8, 9} but not the set {1, 3, 5, 7}.

Problem 18

Defifine the determinant D1 = |1|, the determinant D₂ =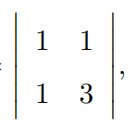and the determinant D₃ =

In general, for positive integer n, let the determinant D_n have 1s in every position of its fifirst row and fifirst column, 3s in the remaining positions of the second row and second column, 5s in the remaining positions of the third row and third column, and so forth. Find the least n so that D_n≥ 2015.

Problem 19

The diagram below shows a 24 × 24 square ABCD. Points E and F lie on sides and , respectively, so that DE = DF = 8. Set X consists of the shaded triangle ABC with its interior, while set Y consists of the shaded triangle DEF with its interior. Set Z consists of all the points that are midpoints of segments connecting a point in set X with a point in set Y . That is, Z = {z | z is the midpoint of xy for x ∈ X and y ∈ Y }. Find the area of the set Z.

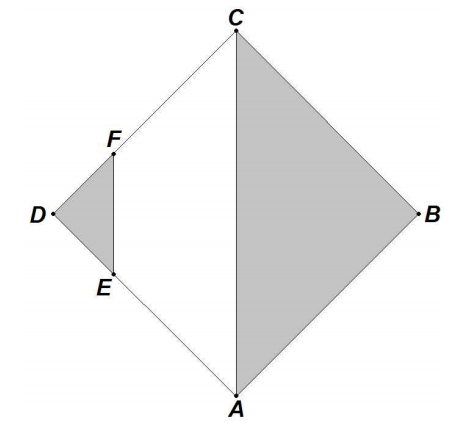
Problem 20

For integers a, b, c, and d the polynomial p(x) = ax3 + bx2 + cx + d satisfifies p(5) + p(25) = 1906. Find the minimum possible value for |p(15)|.

Problem 21

Find the remainder when 2008²⁰¹⁴ + (2014 − 2008)²⁰¹⁴ is divided by 100.

Problem 22

Let x be a real number between 0 and for which the function 3 sin² x + 8 sin x cos x + 9 cos² x obtains its maximum value, M. Find the value of M + 100 cos² x.

Problem 23

Larry and Diane start 100 miles apart along a straight road. Starting at the same time, Larry and Diane drive their cars toward each other. Diane drives at a constant rate of 30 miles per hour. To make it interesting, at the beginning of each 10 mile stretch, if the two drivers have not met, Larry flflips a fair coin. If the coin comes up heads, Larry drives the next 10 miles at 20 miles per hour. If the coin comes up tails, Larry drives the next 10 miles at 60 miles per hour. Larry and Diane stop driving when they meet. The expected number of times that Larry flflips the coin is , where m and n are relatively prime positive integers. Find m + n.

Problem 24

The complex number w has positive imaginary part and satisfifies |w| = 5. The triangle in the complex plane with vertices at w, w² , and w³ has a right angle at w. Find the real part of w³.

Problem 25

You have a collection of small wooden blocks that are rectangular solids measuring 3 × 4 × 6. Each of the six faces of each block is to be painted a solid color, and you have three colors of paint to use. Find the number of distinguishable ways you could paint the blocks. (Two blocks are distinguishable if you cannot rotate one block so that it looks identical to the other block.)

Problem 26

Seven people of seven difffferent ages are attending a meeting. The seven people leave the meeting one at a time in random order. Given that the youngest person leaves the meeting sometime before the oldest person leaves the meeting, the probability that the third, fourth, and fififth people to leave the meeting do so in order of their ages (youngest to oldest) is , where m and n are relatively prime positive integers. Find m + n.

Problem 27

A container is shaped like a right circular cone open at the top surmounted by a frustum which is open at the top and bottom as shown below. The lower cone has a base with radius 2 centimeters and height 6 centimeters while the frustum has bases with radii 2 and 8 centimeters and height 6 centimeters. If there is a rainfall measuring 2 centimeter of rain, the rain falling into the container will fifill the container to a height of m + cm, where m and n are positive integers. Find m + n.

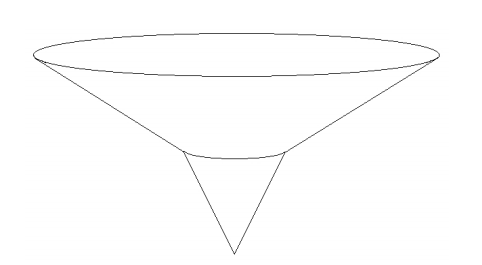
Problem 28

Let A = {1, 2, 3, 4, 5} and B = {0, 1, 2}. Find the number of pairs of functions {f, g} where both f and g map the set A into the set B and there are exactly two elements x ∈ A where f(x) = g(x). For example, the function f that maps 1 → 0, 2 → 1, 3 → 0, 4 → 2, 5 → 1 and the constant function g which maps each element of A to 0 form such a pair of functions.

Problem 29

Ten balls are stacked in a pyramid. The bottom level of the stack has six balls each with radius 6 arranged in a triangular formation with adjacent balls tangent to each other. The middle level of the stack has three balls each with radius 5 arranged in a triangular formation each tangent to three balls in the bottom level. The top level of the stack has one ball with radius 6 tangent to the three balls in the middle level. The diagram shows the stack of ten balls with the balls in the middle shaded. The height of this stack of balls is where m and n are positive integers. Find m + n.

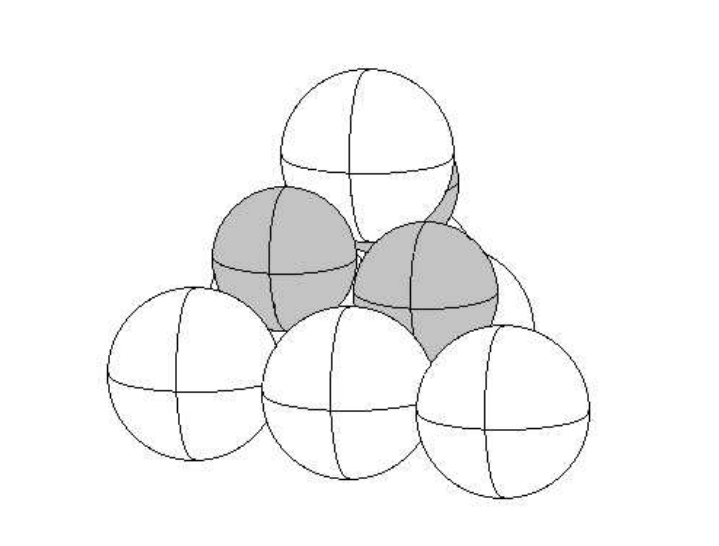
Problem 30

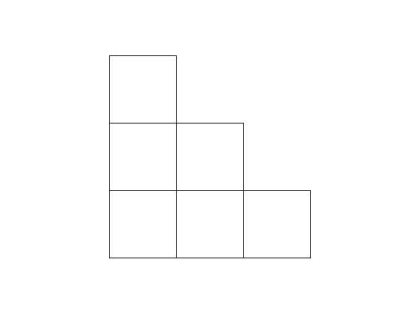
Cindy and Neil wanted to paint the side of a staircase in the six-square pattern shown below so that each of the six squares is painted a solid color, and no two squares that share an edge are the same color. Cindy draws all n patterns that can be colored using the four colors red, white, blue, and green. Neil looked at these patterns and claimed that k of the patterns Cindy drew were incorrect because two adjacent squares were colored with the same color. This is because Neil is color-blind and cannot distinguish red from green. Find n + k.