Home » 国际竞赛 » Details

紫色彗星数学竞赛真题（2014年高中组）

Category: 国际竞赛, 数学国际竞赛 Date: 2021年11月15日下午5:32

PURPLE COMET! MATH MEET April 2014

HIGH SCHOOL - PROBLEMS

Problem 1

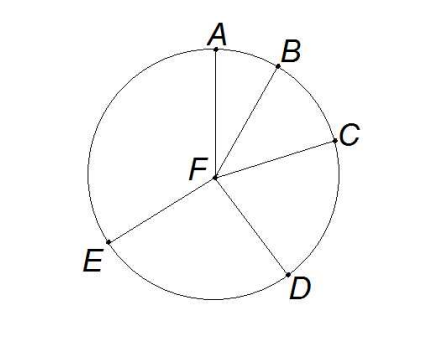
The diagram below shows a circle with center F. The angles are related with ∠BF C = 2∠AF B, ∠CF D = 3∠AF B, ∠DF E = 4∠AF B, and ∠EF A = 5∠AF B. Find the degree measure of ∠BFC.

Problem 2

On the table was a pile of 135 chocolate chips. Phil ate of the chips, Eric ate of the chips, and Beverly ate the rest of the chips. How many chips did Beverly eat?

Problem 3

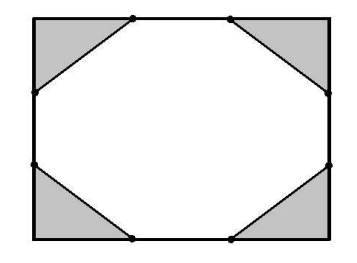
The diagram below shows a rectangle with side lengths 36 and 48. Each of the sides is trisected and edges are added between the trisection points as shown. Then the shaded corner regions are removed, leaving the octagon which is not shaded in the diagram. Find the perimeter of this octagon.

Problem 4

Find the least positive integer n such that the prime factorizations of n, n + 1, and n + 2 each have exactly two factors (as 4 and 6 do, but 12 does not).

Problem 5

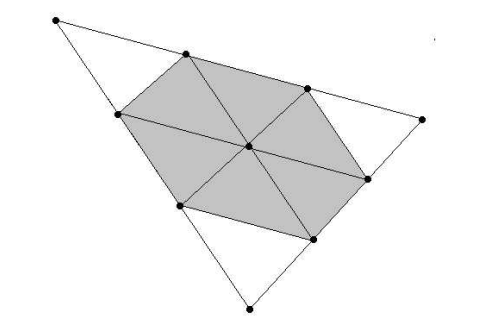
The diagram below shows a large triangle with area 72. Each side of the triangle has been trisected, and line segments have been drawn between these trisection points parallel to the sides of the triangle. Find the area of the shaded region.

Problem 6

Nora drove 82 miles in 90 minutes. She averaged 50 miles per hour for the fifirst half-hour and averaged 55 miles per hour for the last half-hour. What was her average speed in miles per hour over the middle half-hour (during the 30 minutes beginning after the fifirst half-hour)?

Problem 7

Andrea is three times as old as Jim was when Jim was twice as old as he was when the sum of their ages was 47. If Andrea is 29 years older than Jim, what is the sum of their ages now?

Problem 8

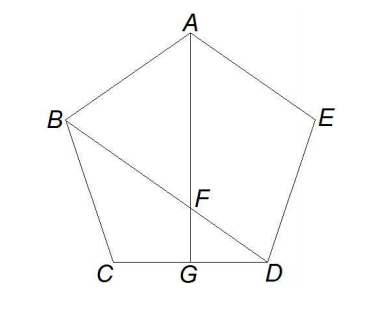
In the diagram below ABCDE is a regular pentagon, is perpendicular to , and intersects at F. Find the degree measure of ∠AFB.

Problem 9

Find n such that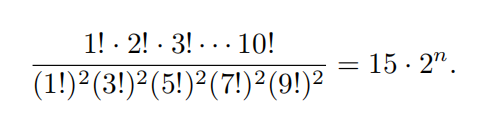

Problem 10

One morning a baker notices that she has 188 cups of flflour and 113 cups of sugar available. Each loaf of bread that the baker makes takes three cups of flflour and a half cup of sugar. Each cake that the baker makes takes two cups of flflour and two cups of sugar. The baker decides to make some loaves of bread and some cakes so that she exactly uses up all of her supplies of flflour and sugar. Find the number of cakes she should make.

Problem 11

How many subsets of {1, 2, 3, 4, . . . , 12} contain exactly one prime number?

Problem 12

The vertices of hexagon ABCDEF lie on a circle. Sides AB = CD = EF = 6, and sides BC = DE = F A = 10. The area of the hexagon is . Find m.

Problem 13

Find n > 0 such that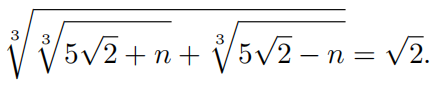

Problem 14

Let a, b, c be positive integers such that abc + bc + c = 2014. Find the minimum possible value of a + b + c.

Problem 15

Find n such that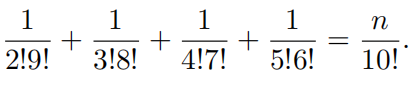

Problem 16

Start with a three-digit positive integer A. Obtain B by interchanging the two leftmost digits of A. Obtain C by doubling B. Obtain D by subtracting 500 from C. Given that A + B + C + D = 2014, fifind A.

Problem 17

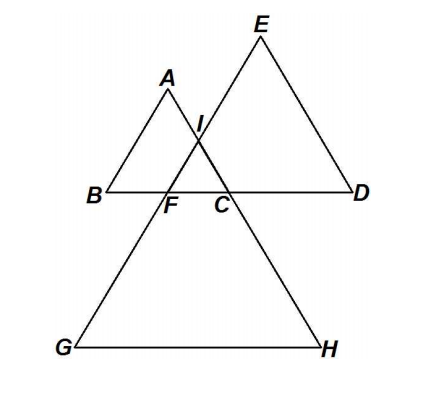
In the fifigure below △ABC, △DEF, and △GHI are overlapping equilateral triangles, C and F lie on ,F and I lie on ，and C and I lie on Length AB = 2F C, DE = 3F C, and GH = 4F C. Given that the area of △FCI is 3, fifind the area of the hexagon ABGHDE.

Problem 18

Let f be a real-valued function such that for every positive real number x. Find f(2014).

Problem 19

Let x, y, and z be positive real numbers satisfying the simultaneous equations

x(y2 + yz + z2 ) = 3y + 10z

y(z2 + zx + x2 ) = 21z + 24x

z(x2 + xy + y2 ) = 7x + 28y.

Find xy + yz + zx.

Problem 20

Triangle ABC has a right angle at C. Let D be the midpoint of side AC, and let E be the intersection of and the bisector of ∠ABC. The area of △ABC is 144, and the area of △DBE is 8. Find AB².

Problem 21

Let a, b, and c be positive integers such that 29a + 30b + 31c = 366. Find 19a + 20b + 21c.

Problem 22

For positive integers m and n, let r(m, n) be the remainder when m is divided by n. Find the smallest positive integer m such that

r(m, 1) + r(m, 2) + r(m, 3) + · · · + r(m, 10) = 4.

Problem 23

Suppose x is a real number satisfying

Find

Problem 24

Let S = 2⁴ + 3⁴ + 5⁴ + 7⁴ + · · · + 17497⁴ be the sum of the fourth powers of the fifirst 2014 prime numbers. Find the remainder when S is divided by 240.

Problem 25

The diagram below shows equilateral △ABC with side length 2. Point D lies on ray so that CD = 4. Points E and F lie on and , respectively, so that E, F, and D are collinear, and the area of 4 AEF is half of the area of △ABC. Then , where m and n are relatively prime positive integers. Find m + 2n.

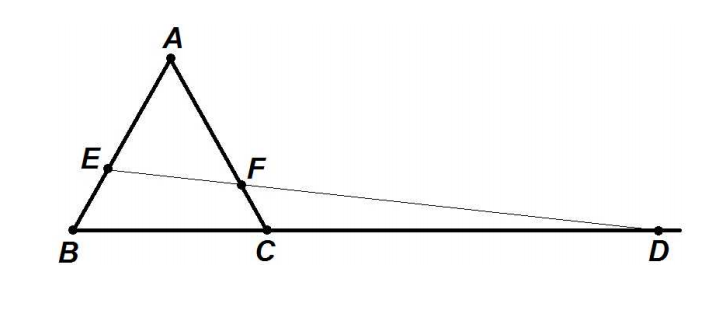
Problem 26

Let ABCD be a cyclic quadrilateral with AB = 1, BC = 2, CD = 3, DA = 4. Find the square of the area of quadrilateral ABCD.

Problem 27

Five men and fifive women stand in a circle in random order. The probability that every man stands next to at least one woman is , where m and n are relatively prime positive integers. Find m + n.

Problem 28

Find the number of ordered triples of positive integers (a, b, c) such that abc divides (ab + 1)(bc + 1)(ca + 1).

Problem 29
Consider the sequences of six positive integers a1, a2, a3, a4, a5, a6 with the properties that a₁ = 1, and if for some j > 1, a_j = m > 1, then m − 1 appears in the sequence a₁, a₂, . . . , a_j−1. Such sequences include 1, 1, 2, 1, 3, 2 and 1, 2, 3, 1, 4, 1 but not 1, 2, 2, 4, 3, 2. How many such sequences of six positive integers are there?

Problem 30

Three mutually tangent spheres each with radius 5 sit on a horizontal plane. A triangular pyramid has a base that is an equilateral triangle with side length 6, has three congruent isosceles triangles for vertical faces, and has height 12. The base of the pyramid is parallel to the plane, and the vertex of the pyramid is pointing downward so that it is between the base and the plane. Each of the three vertical faces of the pyramid is tangent to one of the spheres at a point on the triangular face along its altitude from the vertex of the pyramid to the side of length 6. The distance that these points of tangency are from the base of the pyramid is , where m and n are relatively prime positive integers. Find m + n.