- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
紫色彗星数学竞赛真题(2013年高中组)
PURPLE COMET! MATH MEET April 2013
HIGH SCHOOL - PROBLEMS
Copyright Titu Andreescu and Jonathan Kane
Problem 1
Two years ago Tom was 25% shorter than Mary. Since then Tom has grown 20% taller, and Mary has grown 4 inches taller. Now Mary is 20% taller than Tom. How many inches tall is Tom now?
Problem 2
The following diagram shows an eight-sided polygon ABCDEF GH with side lengths 8, 15, 8, 8, 8, 6, 8, and 29 as shown. All of its angles are right angles. Turn this eight-sided polygon into a six-sided polygon by connecting B to D with an edge and E to G with an edge to form polygon ABDEGH. Find the perimeter of ABDEGH.
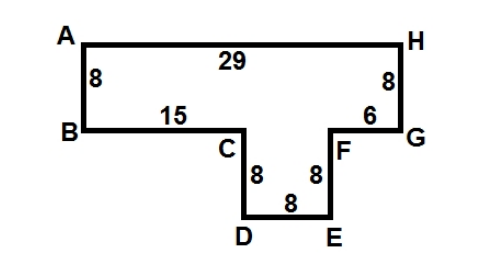
Problem 3
In how many rearrangements of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 do the numbers form a hill, that is, the numbers form an increasing sequence at the beginning up to a peak, and then form a decreasing sequence to the end such as in 129876543 or 258976431?
Problem 4
The greatest common divisor of n and 180 is 12. The least common multiple of n and 180 is 720. Find n.
Problem 5
How many four-digit positive integers have exactly one digit equal to 1 and exactly one digit equal to 3?
Problem 6
In four years Kay will be twice as old as Gordon. Four years after that Shaun will be twice as old as Kay. Four years after that Shaun will be three times as old as Gordon. How many years old is Shaun now?
Problem 7
Find the least six-digit palindrome that is a multiple of 45. Note that a palindrome is a number that reads the same forward and backwards such as 1441 or 35253.
Problem 8
Naomi has three colors of paint which she uses to paint the pattern below. She paints each region a solid color, and each of the three colors is used at least once. If Naomi is willing to paint two adjacent regions with the same color, how many color patterns could Naomi paint?
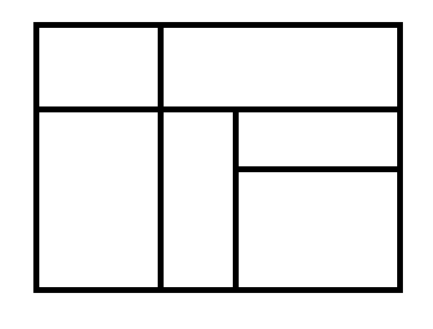
Problem 9
![]() if and only if x is in the interval [a, b]. There are relatively prime positive integers m and n so that b − a =
if and only if x is in the interval [a, b]. There are relatively prime positive integers m and n so that b − a = ![]() . Find m + n.
. Find m + n.
Problem 10
The number N is the product of two primes. The sum of the positive divisors of N that are less than N is 2014. Find N.
Problem 11
After Jennifer walked r percent of the way from her home to the store, she turned around and walked home, got on her bicycle, and bicycled to the store and back home. Jennifer bicycles two and a half times faster than she walks. Find the largest value of r so that returning home for her bicycle was not slower than her walking all the way to and from the store without her bicycle.
Problem 12
How many four-digit positive integers have no adjacent equal even digits? For example, count numbers such as 1164 and 2035 but not 6447 or 5866.
Problem 13
There are relatively prime positive integers m and n so that

Find m + n.
Problem 14
How many ordered triples (a, b, c) of positive integers satisfy a ≤ b ≤ c and a · b · c = 1000?
Problem 15
For what value of x does the following determinant have the value 2013?
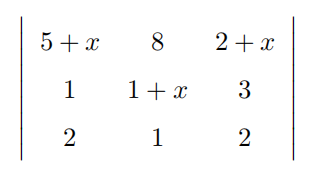
Problem 16
The fifigure below shows a 90 × 90 square with each side divided into three equal segments. Some of the endpoints of these segments are connected by straight lines. Find the area of the shaded region.
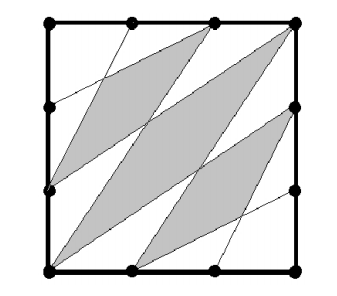
Problem 17
For positive integers m and n, the decimal representation for the fraction ![]() begins 0.711 followed by other digits. Find the least possible value for n.
begins 0.711 followed by other digits. Find the least possible value for n.
Problem 18
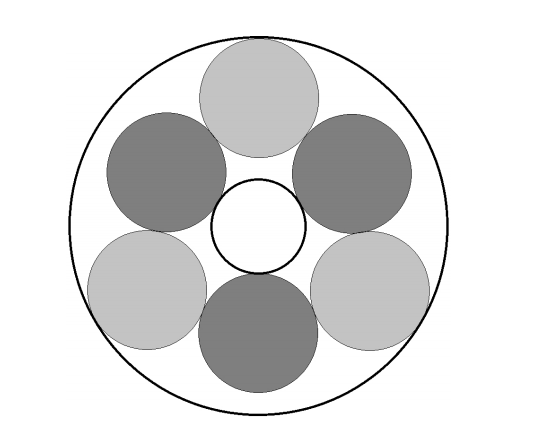
Two concentric circles have radii 1 and 4. Six congruent circles form a ring where each of the six circles is tangent to the two circles adjacent to it as shown. The three lightly shaded circles are internally tangent to the circle with radius 4 while the three darkly shaded circles are externally tangent to the circle with radius 1. The radius of the six congruent circles can be written ![]() , where k, m, and n are integers with k and n relatively prime. Find k + m + n.
, where k, m, and n are integers with k and n relatively prime. Find k + m + n.
Problem 19
There is a pile of eggs. Joan counted the eggs, but her count was offff by 1 in the 1’s place. Tom counted the eggs, but his count was offff by 1 in the 10’s place. Raoul counted the eggs, but his count was offff by 1 in the 100’s place. Sasha, Jose, Peter, and Morris all counted the eggs and got the correct count. When these seven people added their counts together, the sum was 3162. How many eggs were in the pile?
Problem 20
Let z be a complex number satisfying ![]() . Evaluate
. Evaluate ![]()
Problem 21
Evaluate (2 − sec2 1° )(2 − sec2 2° )(2 − sec2 3°)· · ·(2 − sec2 89°).
Problem 22
Find the least three-digit number that is equal to the sum of its digits plus twice the product of its digits.
Problem 23
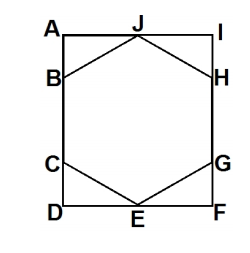
The diagram below shows the regular hexagon BCEGHJ surrounded by the rectangle ADF I. Let θ be the measure of the acute angle between the side ![]() of the hexagon and the diagonal of the rectangle
of the hexagon and the diagonal of the rectangle ![]() . There are relatively prime positive integers m and n so that sin2 θ =
. There are relatively prime positive integers m and n so that sin2 θ = ![]() . Find m + n.
. Find m + n.
Problem 24
Find the remainder when 333333 is divided by 33.
Problem 25
In how many ways can you write 12 as an ordered sum of integers where the smallest of those integers is equal to 2? For example, 2 + 10, 10 + 2, and 3 + 2 + 2 + 5 are three such ways.
Problem 26
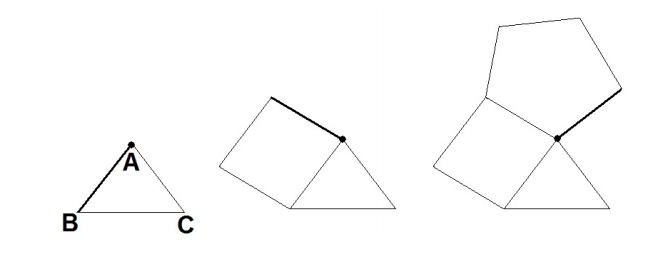
The diagram below shows the fifirst three fifigures of a sequence of fifigures. The fifirst fifigure shows an equilateral triangle ABC with side length 1. The leading edge of the triangle going in a clockwise direction around A is labeled ![]() and is darkened in on the fifigure. The second fifigure shows the same equilateral triangle with a square with side length 1 attached to the leading clockwise edge of the triangle. The third fifigure shows the same triangle and square with a regular pentagon with side length 1 attached to the leading clockwise edge of the square. The fourth fifigure in the sequence will be formed by attaching a regular hexagon with side length 1 to the leading clockwise edge of the pentagon. The hexagon will overlap the triangle. Continue this sequence through the eighth fifigure. After attaching the last regular fifigure (a regular decagon), its leading clockwise edge will form an angle of less than 180° with the side
and is darkened in on the fifigure. The second fifigure shows the same equilateral triangle with a square with side length 1 attached to the leading clockwise edge of the triangle. The third fifigure shows the same triangle and square with a regular pentagon with side length 1 attached to the leading clockwise edge of the square. The fourth fifigure in the sequence will be formed by attaching a regular hexagon with side length 1 to the leading clockwise edge of the pentagon. The hexagon will overlap the triangle. Continue this sequence through the eighth fifigure. After attaching the last regular fifigure (a regular decagon), its leading clockwise edge will form an angle of less than 180° with the side ![]() of the equilateral triangle. The degree measure of that angle can be written in the form
of the equilateral triangle. The degree measure of that angle can be written in the form ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 27
Suppose a, b, and c are real numbers that satisfy a + b + c = 5 and ![]() . Find the greatest possible value of a3 + b3 + c3.
. Find the greatest possible value of a3 + b3 + c3.
Problem 28
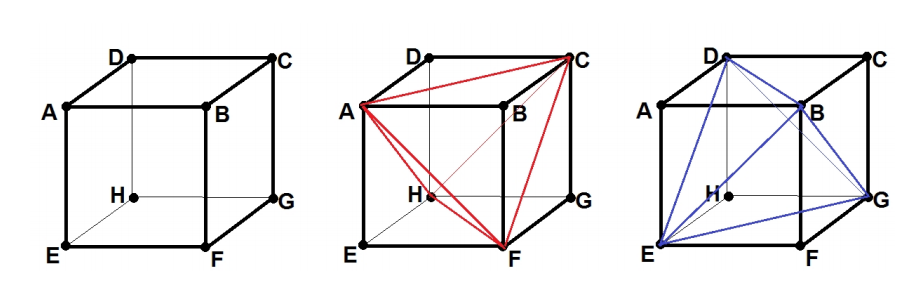
Let A, B, C, D, E, F, G, H be the eight vertices of a 30 × 30 × 30 cube as shown. The two fifigures ACFH and BDEG are congruent regular tetrahedra. Find the volume of the intersection of these two tetrahedra.
Problem 29
You can tile a 2 × 5 grid of squares using any combination of three types of tiles: single unit squares, two side by side unit squares, and three unit squares in the shape of an L. The diagram below shows the grid, the available tile shapes, and one way to tile the grid. In how many ways can the grid be tiled?
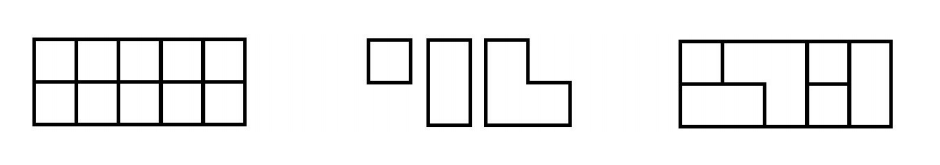
Problem 30
Suppose x, y, and z are integers that satisfy the system of equations
x2y + y2z + z2x = 2186
xy2 + yz2 + zx2 = 2188.
Evaluate x2 + y2 + z2.
扫描下方二维码获取本年度学术活动答案及解析
还可免费领取最新年度真题及答案解析


早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








