- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2021年11月AMC12考试 A卷 真题及解析
AMC12A Problems
What is the value of 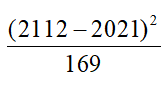 ?
?
(A) 7 (B) 21 (C) 49 (D) 64 (E) 91
Menkara has a 46 index card. If she shortens the length of one side of this card by 1 inch, the card would have area 18 square inches. What would the area of the card be in square inches if instead she shortens the length of the other side by 1 inch?
(A) 16 (B) 17 (C) 18 (D) 19 (E) 20
Mr. Lopez has a 4X6 choice of two routes to get to work. Route A is 6 miles long, and his average speed along this route is 30 miles per hour. Route B is 5 miles long, and his average speed along this route is 40 miles per hour, except for a ![]() -mile stretch in a school zone where his average speed is 20 miles per hour. By how many minutes is Route B quicker than Route A?
-mile stretch in a school zone where his average speed is 20 miles per hour. By how many minutes is Route B quicker than Route A?
The six-digit number ![]() is prime for only one digit A. what is A?
is prime for only one digit A. what is A?
(A) 1 (B) 3 (C) 5 (D) 7 (E) 9
Elmer the emu takes 44 equal strides to walk between consecutive telephone poles on a rural road. Oscar the ostrich can cover the same distance in 12 equal leaps. The telephone poles are evenly spaced, and the 41st pole along this road is exactly one mile (5280 feet) from the first pole. How much longer, in feet, is Oscar’s leap than Elmer’s stride?
(A) 6 (B) 8 (C) 10 (D) 11 (E) 15
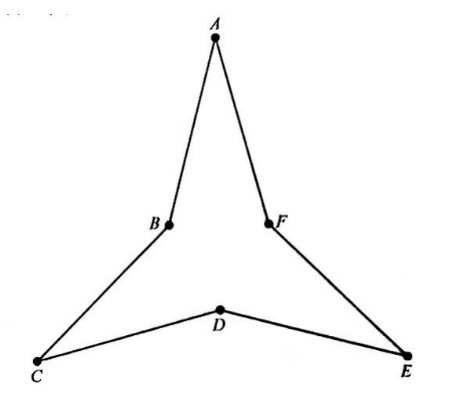
As shown in the figure below, point Elies in the opposite half-plane deter-mined by line CDfrom point A so that ∠CDE=110°. Point F lies on ![]() so that DE=DF, and ABCD is a square. What is the degree measure of ∠AFE?
so that DE=DF, and ABCD is a square. What is the degree measure of ∠AFE?
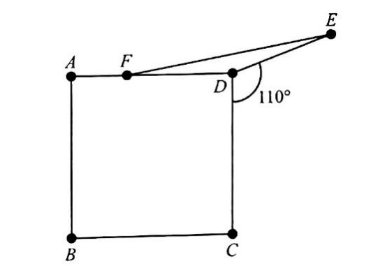
(A) 160 (B) 164 (C) 166 (D) 170 (E) 174
A school has 100 students and 5 teachers. In the first period, each student is taking one class, and each teacher is teaching one class. The enrollments in the classes are 50, 20, 20, 5, and 5. Lettbe the average value obtained if a teacher is picked at random and the number of students in their class is noted. Let s be the average value obtained if a student is picked at random and the number of students in their class, including that student, is noted. What is t-s?
(A) -18.5 (B) -13.5 (C) 0 (D) 13.5 (E) 18.5
Let Mbe the least common multiple of all the integers 10 through 30, inclusive. Let Nbe the least common multiple of M, 32, 33, 34, 35, 36, 37, 38, 39, and 40. What is the value of ![]() ?
?
(A) 1 (B) 2 (C) 37 (D) 74 (E) 2886
A right rectangular prism whose surface area and volume are numerically equal has edge lengths log2X , log3X and log 4 X. What is x?
The base-nine representation of the number Nis 27,006,000,052nine. What is the remainder when N is divided by 5?
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
1 Consider two concentric circles of radius 17 and radius 19. The larger circle has a chord, half of which lies inside the smaller circle. What is the length of the chord in the larger circle?
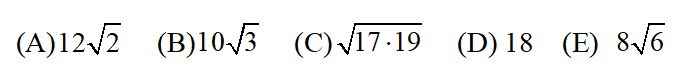
1 What is the number of terms with rational coefficients among the 1001 terms in the expansion of ![]() ?
?
(A) 0 (B) 166 (C) 167 (D) 500 (E) 501
The angle bisector of the acute angle formed at the origin by the graphs of the lines y=xand y=3xhas equation y=kx. What is k?
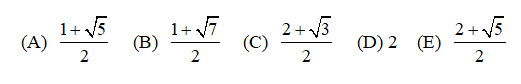
In the figure, equilateral hexagon ABCDEFhas three nonadjacent acute interior angles that each measure 30°. The enclosed area of the hexagon is ![]() . What is the perimeter of the hexagon?
. What is the perimeter of the hexagon?
(A) 4 (B) ![]() (C) 12 (D) 18 (E)
(C) 12 (D) 18 (E)![]()
Recall that the conjugate of the complex number w=a+bi, where aand bare real numbers and i=![]() , is the complex number
, is the complex number ![]() . For any complex number z, let
. For any complex number z, let ![]() . The polynomial
. The polynomial ![]() has four complex roots:Z 1 Z 2 Z 3 and Z 4. Let
has four complex roots:Z 1 Z 2 Z 3 and Z 4. Let ![]() be the polynomial whose roots are f(Z 1) , f(Z 2) ,f(Z 3) ,and f(Z 4) , where the coefficients A, B, C, and D are complex numbers. What is B+D?
be the polynomial whose roots are f(Z 1) , f(Z 2) ,f(Z 3) ,and f(Z 4) , where the coefficients A, B, C, and D are complex numbers. What is B+D?
(A) -304 (B) -208 (C) 12i (D) 208 (E) 304
1 An organization has 30 employees, 20 of whom have a brand A computerwhile the other 10 have a brand B computer. For security, the computerscan only be connected to each other and only by cables. The cables can only connect a brand A computer to a brand B computer. Employees can communicate with each other if their computers are directly connected by a cable or by relaying messages through a series of connected computers. Initially. no computer is connected to any other. A technician arbitrarily selects one computer of each brand and installs a cable between them, provided there is not already a cable between that pair. The technician stops once every employee can communicate with every other. What is the maximum possible number of cables used?
(A) 190 (B) 191 (C) 192 (D) 195 (E) 196
For how many ordered pairs (b,c) of positive integers does neither x2 + bx + c = 0 nor x2 + cx + b = 0 have two distinct real solutions?
(A) 4 (B) 6 (C) 8 (D) 12 (E) 16
Each of 20 balls is tossed independently and at random into one of 5 bins. Let p be the probability that some bin ends up with 3 balls, another with 5 balls, and the other three with 4 balls each. Let q be the probability that every bin ends up with 4 balls. What is ![]() ?
?
(A) 1 (B) 4 (C) 8 (D) 12 (E) 16
Let x be the least real number greater than 1 such that sinx = sin(x 2), where the arguments are in degrees, what is x rounded up to the closest integer?
(A) 10 (B) 13 (C) 14 (D) 19 (E) 20
For each positive integer n, let f 1(n) be twice the number of positive integer divisors of n, and for j≥2, let ![]() . For how many values of n≤ 50 is
. For how many values of n≤ 50 is ![]()
(A) 7 (B) 8 (C) 9 (D) 10 (E) 11
Let ABCD be an isosceles trapezoid with ![]() and AB=CD. Points X and Y lie on diagonal
and AB=CD. Points X and Y lie on diagonal ![]() with X between A and Y, as shown in the figure. Suppose ∠AXD =∠BYC =90°, AX=3, XY=1, and YC=2. What is the area of ABCD?
with X between A and Y, as shown in the figure. Suppose ∠AXD =∠BYC =90°, AX=3, XY=1, and YC=2. What is the area of ABCD?
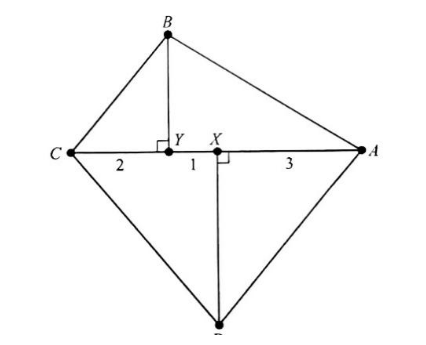
(A) 15 (B) (C) (D) 18 (E)
Azar and Carl play a game of tic-tac-toe. Azar places an X in one of the boxes in a 3-by-3 array of boxes, then Carl places an O in one of the remaining boxes, After that, Azar places an X in one of the remaining boxes, and so on until all 9 boxes are filled or one of the players has 3 of their symbols in a row-horizontal, vertical, or diagonal-whichever comes first, in which case that player wins the games. Suppose the players make their moves at random, rather than trying to follow a rational strategy, and that Carl wins the game when he places his third O. how many ways can the board look after the game is over?
(A) 36 (B) 112 (C) 120 (D) 148 (E) 160
A quadratic polynomial p(x) with real coefficients and leading coefficient 1 is called disrespectful if the equation p(p(x)) = 0 is satisfied by exactly three real numbers. Among all the disrespectful quadratic polynomials, there is a unique such polynomial ![]() for which the sum of the roots is maximized. What is
for which the sum of the roots is maximized. What is ![]() ?
?
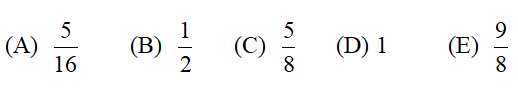
Convex quadrilateral ABCD has AB=18, ∠A = 60° , and ![]() . In some order, the lengths of the four sides form an arithmetic progression, and side
. In some order, the lengths of the four sides form an arithmetic progression, and side ![]() is a side of maximum length. The length of another side is a. what is the sum of all possible values of a?
is a side of maximum length. The length of another side is a. what is the sum of all possible values of a?
(A) 24 (B) 42 (C) 60 (D) 66 (E) 84
Let m≥ 5 be an odd integer, and let D(m) denote the number of quadruples (a1, a 2,a 3,a 4)of distinct 1≤ ai ≤m integers with for all i such that m divides a 1+a 2+a 3+a 4. There is a polynomial ![]() such that D(m)= q(m) for all odd integers m ≥ 5. What is C 1?
such that D(m)= q(m) for all odd integers m ≥ 5. What is C 1?
(A) -6 (B) -1 (C) 4 (D) 6 (E) 11
| 1.C | 2.E | 3.B | 4.E | 5.B |
| 6.D | 7.B | 8.D | 9.E | 10.D |
| 11.E | 12.C | 13.A | 14.E | 15.D |
| 16.B | 17.B | 18.E | 19.B | 20.D |
| 21.C | 22.D | 23.A | 24.D | 25.E |
扫描下方二维码获取学术活动答案及解析

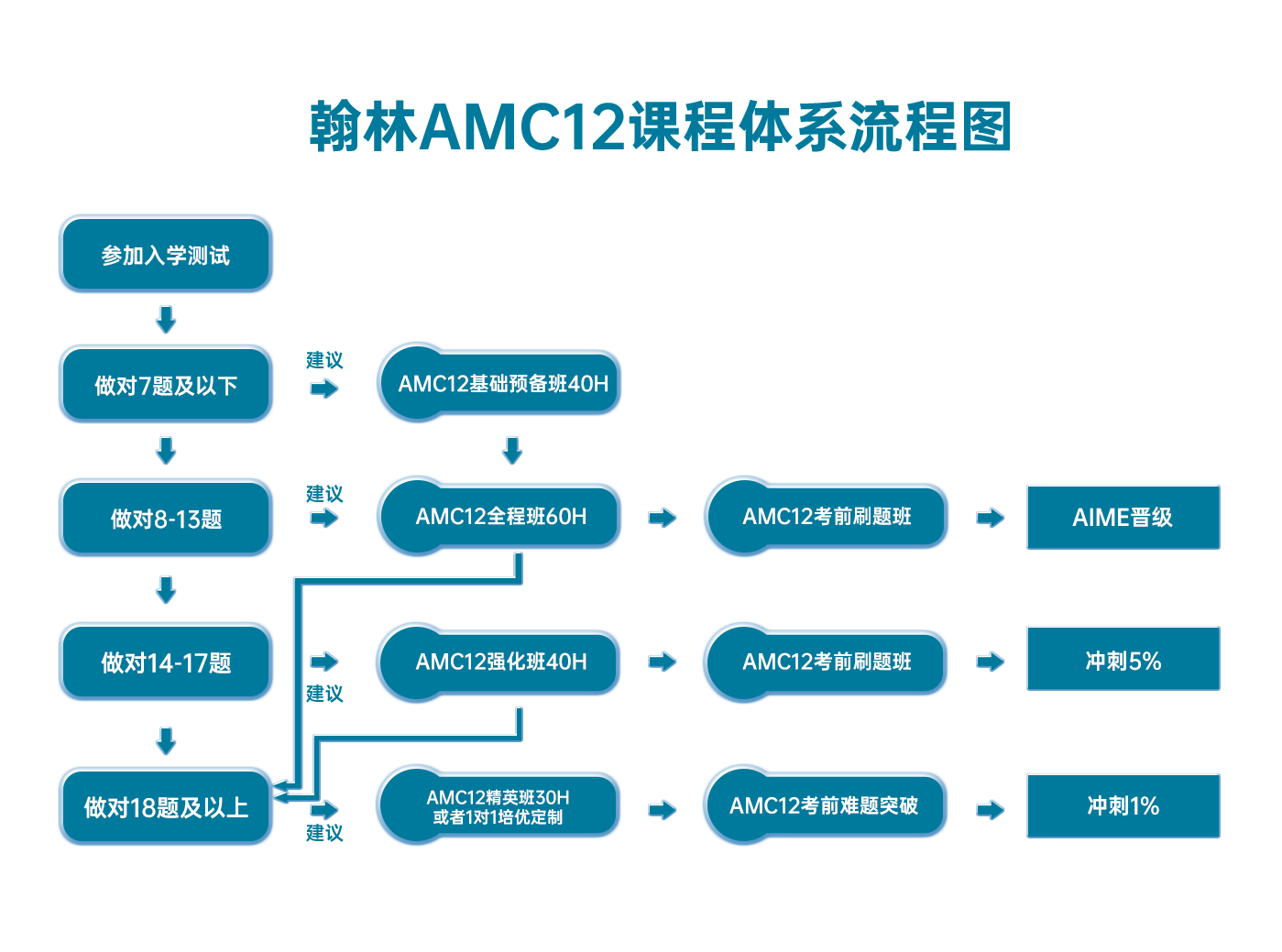
翰林AMC12课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









