- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2021年11月AMC10 A试题及答案公布
2021年AMC10 A试题
答案见文末,如有疑问,可扫码咨询,免费领取近几年AMC真题及解析
1. What is the value of ![]() ?
?
(A) 7 (B) 21 (C) 49 (D) 64 (E) 91
2. Menkara has a 4x6 index card. If she shortens the length of one side of this card by 1 inch, the card would have area 18 square inches. What would the area of the card be in square inches if instead she shortens the length of the other side by 1 inch?
(A) 16 (B) 17 (C) 18 (D) 19 (E) 20
3. What is the maximum number of balls of clay with radius 2 that can completely fit inside a cube of side length 6 assuming that the balls can be reshaped but not compressed before they are packed in the cube?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
4. Mr. Lopez has a choice of two routes to get to work. Route A is 6 miles long, and his average speed along this route is 30 miles per hour. Route B is 5 miles long, and his average speed along this route is 40 miles per hour, except for a ![]() -mile stretch in a school zone where his average speed is 20 miles per hour. By how many minutes is Route B quicker than Route A?
-mile stretch in a school zone where his average speed is 20 miles per hour. By how many minutes is Route B quicker than Route A?

5. The six-digit number ![]() is prime for only one digit A. what is A?
is prime for only one digit A. what is A?
(A) 1 (B) 3 (C) 5 (D) 7 (E) 9
6. Elmer the emu takes 44 equal strides to walk between consecutive telephone poles on a rural road. Oscar the ostrich can cover the same distance in 12 equal leaps. The telephone poles are evenly spaced, and the 41st pole along this road is exactly one mile (5280 feet) from the first pole. How much longer, in feet, is Oscar’s leap than Elmer’s stride?
(A) 6 (B) 8 (C) 10 (D) 11 (E) 15
7. As shown in the figure below, point E lies in the opposite half-plane deter-mined by line CD from point A so that ![]() . Point F lies on
. Point F lies on ![]() so that DE=DF, and ABCD is a square. What is the degree measure of
so that DE=DF, and ABCD is a square. What is the degree measure of ![]() ?
?

(A) 160 (B) 164 (C) 166 (D) 170 (E) 174
8. A two-digit positive integer is said to be cuddly if it is equal to the sum of its nonzero tens digit and the square of its units digit. How many two-digit positive integers are cuddly?
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
9. When a certain unfair die is rolled, an even number is 3 times as likely to appear as an odd number. The die is rolled twice. What is the probability that the sum of the numbers rolled is even?
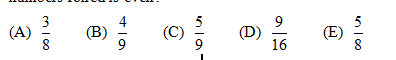
10. A school has 100 students and 5 teachers. In the first period, each student is taking one class, and each teacher is teaching one class. The enrollments in the classes are 50, 20, 20, 5, and 5. Let t be the average value obtained if a teacher is picked at random and the number of students in their class is noted. Let s be the average value obtained if a student is picked at random and the number of students in their class, including that student, is noted. What is t-s?
(A) -18.5 (B) -13.5 (C) 0 (D) 13.5 (E) 18.5
11. Emily sees a ship traveling at a constant speed along a straight section of a river. She walks parallel to the riverbank at a uniform rate faster than the ship. She counts 210 equal steps walking from the back of the ship to the front. Walking in the opposite direction, she counts 42 steps of the same size from the front of the ship to the back. In terms of Emily’s equal steps, what is the length of the ship?
(A) 70 (B) 84 (C) 98 (D) 105 (E) 126
12. The base-nine representation of the number N is 27,006,000,052nine. What is the remainder when N is divided by 5?
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
13. Each of 6 balls is randomly and independently painted either black or white with equal probability. What is the probability that every ball is different in color from more than half of the other 5 balls?
![]()
14. How many ordered pairs (x,y) of real numbers satisfy the following system of equations?
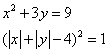
(A) 1 (B) 2 (C) 3 (D) 5 (E) 7
15. Isosceles triangle ABC has AB=AC=![]() , and a circle with radius
, and a circle with radius ![]() is tangent to line AB at B and to line AC at C. What is the area of the circle that passes through vertices A, B, and C?
is tangent to line AB at B and to line AC at C. What is the area of the circle that passes through vertices A, B, and C?
(A)24π (B)25π (C)26π (D)27π (E)28π
16. The graph of ![]() is symmetric about which of the following? (Here
is symmetric about which of the following? (Here ![]() is the greatest integer not exceeding x?
is the greatest integer not exceeding x?
(A) the y-axis (B) the line x=1 (C) the origin (D) the point ![]() (E) the point (1,0)
(E) the point (1,0)
17. An architect is building a structure that will place vertical pillars at the vertices of regular hexagon ABCDEF, which is lying horizontally on the ground. The six pillars will hold up a flat solar panel that will not be parallel to the ground. The heights of the pillars at A, B, and C are 12, 9, and 10 meters, respectively. What is the height, in meters, of the pillar at E?
![]()
18. A farmer’s rectangular field is partitioned into a 2 by 2 grid of 4 rectangular sections as shown in the figure. In each section the farmer will plant one crop: corn, wheat, soybeans, or potatoes. The farmer does not want to grow corn and wheat in any two sections that share a border, and the farmer does not want to grow soybeans and potatoes in any two sections that share a border. Given these restrictions, in how many ways can the farmer choose crops to plant in each of the four sections of the field?
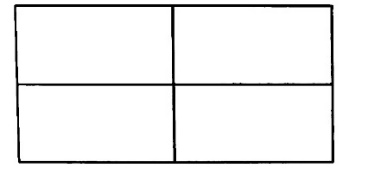
(A) 12 (B) 64 (C) 84 (D) 90 (E) 144
19. A disk of radius 1 rolls all the way around the inside of a square of side length s>4 and sweeps out a region of area A. A second disk of radius 1 rolls all the way around the outside of the same square and sweeps out a region of area 2A. The value of s can be written as ![]() , where a, b, and c are positive integers and b and c are relatively prime. What is a+b+c?
, where a, b, and c are positive integers and b and c are relatively prime. What is a+b+c?
(A) 10 (B) 11 (C) 12 (D) 13 (E) 14
20. For how many ordered pairs (b,c) of positive integers does neither ![]() nor
nor ![]() have two distinct real solutions?
have two distinct real solutions?
(A) 4 (B) 6 (C) 8 (D) 12 (E) 16
21. Each of 20 balls is tossed independently and at random into one of 5 bins. Let p be the probability that some bin ends up with 3 balls, another with 5 balls, and the other three with 4 balls each. Let q be the probability that every bin ends up with 4 balls. What is ![]() ?
?
(A) 1 (B) 4 (C) 8 (D) 12 (E) 16
22. Inside a right circular cone with radius 5 and height 12 are three congruent spheres each with radius r. Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. What is r?

23. For each positive integer n2, let ![]() be twice the number of positive integer divisors of n2, and for
be twice the number of positive integer divisors of n2, and for ![]() , let
, let ![]() . For how many values of
. For how many values of ![]() is
is ![]() ?
?
(A) 7 (B) 8 (C) 9 (D) 10 (E) 11
24. Each of the 12 edges of a cube is labeled 0 or 1. Two labelings are considered different even if one can be obtained from the other by a sequence of one or more rotations and/or reflections. For how many such labelings is the sum of the labels on the edges of each of the 6 faces of the cube equal to 2?
(A) 8 (B) 10 (C) 12 (D) 16 (E) 20
25. A quadratic polynomial ![]() with real coefficients and leading coefficient 1 is called disrespectful if the equation
with real coefficients and leading coefficient 1 is called disrespectful if the equation ![]() is satisfied by exactly three real numbers. Among all the disrespectful quadratic polynomials, there is a unique such polynomial
is satisfied by exactly three real numbers. Among all the disrespectful quadratic polynomials, there is a unique such polynomial ![]() for which the sum of the roots is maximized. What is
for which the sum of the roots is maximized. What is ![]() ?
?

2021 AMC10 A试题 答案:
| 1.C | 2.E | 3.D | 4.B | 5.E |
| 6.B | 7.D | 8.B | 9.E | 10.B |
| 11.A | 12.D | 13.D | 14.D | 15.C |
| 16.D | 17.D | 18.C | 19.A | 20.B |
| 21.E | 22.B | 23.D | 24.E | 25.A |


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








