Home » 国际竞赛 » Details

紫色彗星数学竞赛真题（2012年高中组）

Category: 国际竞赛, 数学国际竞赛 Date: 2021年11月11日下午4:55

PURPLE COMET MATH MEET April 2012

HIGH SCHOOL - PROBLEMS

Problem 1

Last month a pet store sold three times as many cats as dogs. If the store had sold the same number of cats but eight more dogs, it would have sold twice as many cats as dogs. How many cats did the pet store sell last month?

Problem 2

What is the greatest three-digit divisor of 111777?

Problem 3

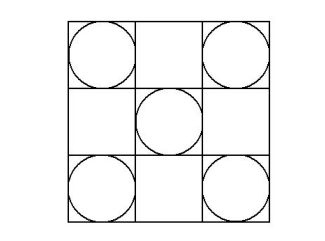
The diagram below shows a large square divided into nine congruent smaller squares. There are circles inscribed in fifive of the smaller squares. The total area covered by all the fifive circles is 20π. Find the area of the large square.

Problem 4

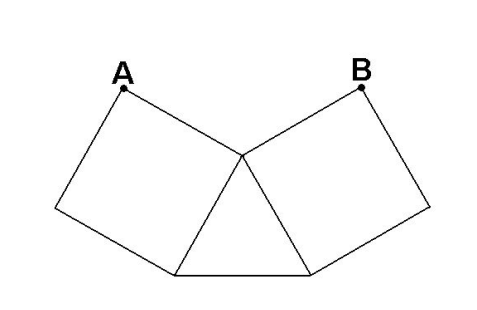
The following diagram shows an equilateral triangle and two squares that share common edges. The area of each square is 75. Find the distance from point A to point B.

Problem 5

Find the sum of the squares of the values x that satisfy

Problem 6

Find the least positive integer n so that both n and n + 1 have prime factorizations with exactly four (not necessarily distinct) prime factors.

Problem 7

Two convex polygons have a total of 33 sides and 243 diagonals. Find the number of diagonals in the polygon with the greater number of sides.

Problem 8

In the tribe of Zimmer, being able to hike long distances and knowing the roads through the forest are both extremely important, so a boy who reaches the age of manhood is not designated as a man by the tribe until he completes an interesting rite of passage. The man must go on a sequence of hikes. The fifirst hike is a 5 kilometer hike down the main road. The second hike is a kilometer hike down a secondary road. Each hike goes down a difffferent road and is a quarter kilometer longer than the previous hike. The rite of passage is completed at the end of the hike where the cumulative distance walked by the man on all his hikes exceeds 1000 kilometers. So in the tribe of Zimmer, how many roads must a man walk down, before you call him a man?

Problem 9

Find the value of x that satisfifies log₃ (log₉ x) = log₉ (log₃ x).

Problem 10

Consider a sequence of eleven squares that have side lengths 3, 6, 9, 12, . . . , 33. Eleven copies of a single square each with area A have the same total area as the total area of the eleven squares of the sequence. Find A.

Problem 11

Defifine f(x) = 2x + 3 and suppose that

g(x + 2) = f (f(x − 1) · f(x + 1) + f(x)). Find g(6).

Problem 12

Ted flflips seven fair coins. There are relatively prime positive integers m and n so that is the probability that Ted flflips at least two heads given that he flflips at least three tails. Find m + n.

Problem 13

Find the least n for which n!(n + 1)!(2n + 1)! − 1 ends in thirty digits that are all 9’s

Problem 14

A circle in the fifirst quadrant with center on the curve y = 2x2 − 27 is tangent to the y-axis and the line 4x = 3y. The radius of the circle is where m and n are relatively prime positive integers. Find m + n.

Problem 15

Let N be a positive integer whose digits add up to 23. What is the greatest possible product the digits of N can have?

Problem 16

Let a, b, and c be non-zero real numbers such that and . There are relatively prime positive integers m and n so that Find m + n.

Problem 17

How many positive integer solutions are there to w + x + y + z = 20 where w + x ≥ 5 and y + z ≥ 5?

Problem 18

Find the number of three-digit numbers such that its fifirst two digits are each divisible by its third digit.

Problem 19

Find the remainder when 259 + 592 + 925 is divided by 11.

Problem 20

Square ABCD has side length 68. Let E be the midpoint of segment , and let F be the point on segment a distance 17 from point A. Point G is on segment so that is perpendicular to segment The length of segment can be written as where m and n are positive integers, and n is not divisible by the square of any prime. Find m + n.

Problem 21

Each time you click a toggle switch, the switch either turns from offff to on or from on to offff. Suppose that you start with three toggle switches with one of them on and two of them offff. On each move you randomly select one of the three switches and click it. Let m and n be relatively prime positive integers so that is the probability that after four such clicks, one switch will be on and two of them will be offff. Find m + n.

Problem 22

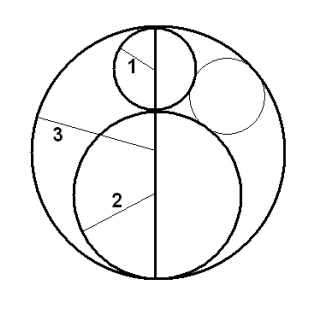
The diagram below shows circles radius 1 and 2 externally tangent to each other and internally tangent to a circle radius 3. There are relatively prime positive integers m and n so that a circle radius is internally tangent to the circle radius 3 and externally tangent to the other two circles as shown. Find m + n.

Problem 23

Find the greatest seven-digit integer divisible by 132 whose digits, in order, are 2, 0, x, y, 1, 2, z where x, y, and z are single digits.

Problem 24

There are positive integers m and n so that x =m+ is a solution to the equation x² − 10x + 1 = .Find m + n.

Problem 25

Find the largest prime that divides 1 · 2 · 3 + 2 · 3 · 4 + ... + 44 · 45 · 46.

Problem 26

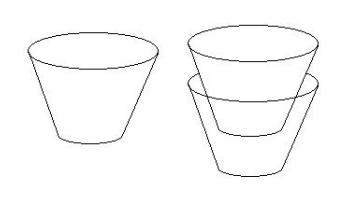
A paper cup has a base that is a circle with radius r, a top that is a circle with radius 2r, and sides that connect the two circles with straight line segments as shown below. This cup has height h and volume V . A second cup that is exactly the same shape as the fifirst is held upright inside the fifirst cup so that its base is a distance of from the base of the fifirst cup. The volume of liquid that will fifit inside the fifirst cup and outside the second cup can be written · V where m and n are relatively prime positive integers. Find m + n.

Problem 27

You have some white one-by-one tiles and some black and white two-by-one tiles as shown below. There are four difffferent color patterns that can be generated when using these tiles to cover a three-by-one rectangle by laying these tiles side by side (WWW, BWW, WBW, WWB). How many difffferent color patterns can be generated when using these tiles to cover a ten-by-one rectangle?

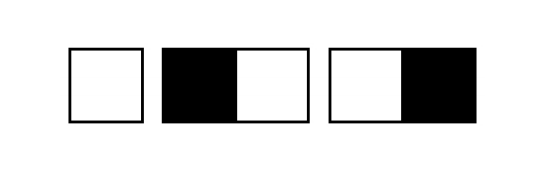
Problem 28

A bag contains 8 green candies and 4 red candies. You randomly select one candy at a time to eat. If you eat fifive candies, there are relatively prime positive integers m and n so that is the probability that you do not eat a green candy after you eat a red candy. Find m + n.

6Problem 29

Let A = {1, 3, 5, 7, 9} and B = {2, 4, 6, 8, 10}. Let f be a randomly chosen function from the set A ∪ B into itself. There are relatively prime positive integers m and n such that is the probability that f is a one-to-one function on A ∪ B given that it maps A one-to-one into A ∪ B and it maps B one-to-one into A ∪ B. Find m + n.

Problem 30

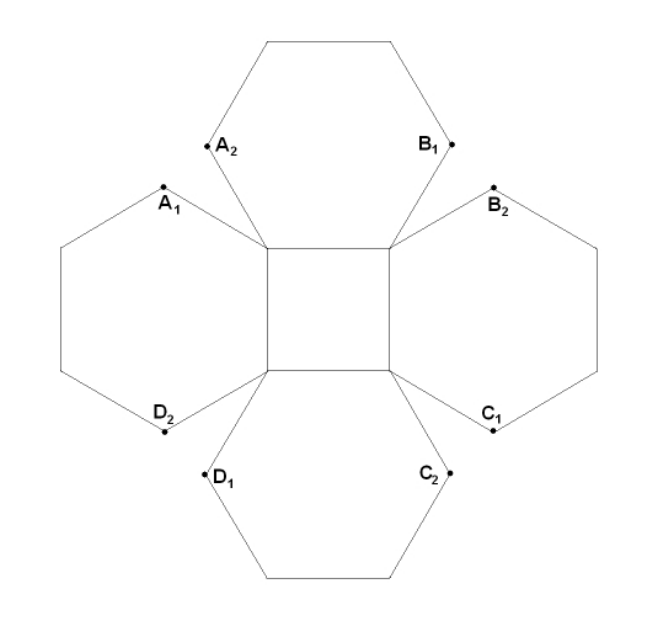
The diagram below shows four regular hexagons each with side length 1 meter attached to the sides of a square. This fifigure is drawn onto a thin sheet of metal and cut out. The hexagons are then bent upward along the sides of the square so that A1 meets A2, B1 meets B2, C1 meets C2, and D1 meets D2. The resulting dish is set on a table with the square lying flflat on the table. If this dish is fifilled with water, the water will rise to the height of the corner where the A1 and A2 meet. There are relatively prime positive integers m and n so that the number of cubic meters of water the dish will hold is . Find m + n.