Home » 国际竞赛 » Details

紫色彗星数学竞赛真题（2011年高中组）

Category: 国际竞赛, 数学国际竞赛 Date: 2021年11月11日下午4:31

PURPLE COMET MATH MEET April 2011

HIGH SCHOOL - PROBLEMS

Problem 1

The ratio of 3 to the positive number n is the same as the ratio of n to 192. Find n.

Problem 2

The target below is made up of concentric circles with diameters 4, 8, 12, 16, and 20. The area of the dark region is nπ. Find n.

Problem 3

Shirley went to the store planning to buy 120 balloons for 10 dollars. When she arrived, she was surprised to fifind that the balloons were on sale for 20 percent less than expected. How many balloons could Shirley buy for her 10 dollars?

Problem 4

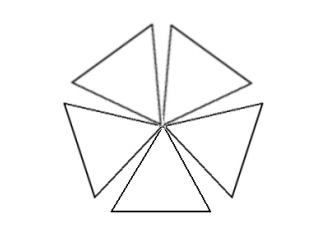
Five non-overlapping equilateral triangles meet at a common vertex so that the angles between adjacent triangles are all congruent. What is the degree measure of the angle between two adjacent triangles?

Problem 5

Let a1 = 2, and for n ≥ 1, let a_n+1 = 2a_n + 1. Find the smallest value of an an that is not a prime number.

Problem 6

Working alone, the expert can paint a car in one day, the amateur can paint a car in two days, and the beginner can paint a car in three days. If the three painters work together at these speeds to paint three cars, it will take them days where m and n are relatively prime positive integers. Find m + n.

Problem 7

Find the prime number p such that 71p + 1 is a perfect square.

Problem 8

When 126 is added to its reversal, 621, the sum is 126 + 621 = 747. Find the greatest integer which when added to its reversal yields 1211.

Problem 9

There are integers m and n so that 9 + is a root of the polynomial x² + mx + n. Find m + n.

Problem 10

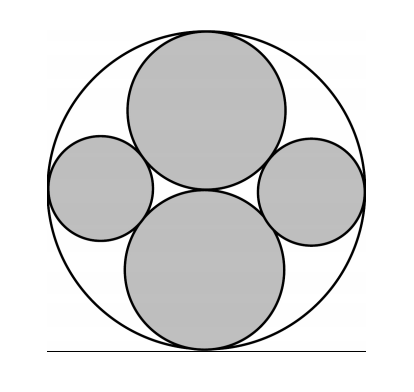
The diagram shows a large circular dart board with four smaller shaded circles each internally tangent to the larger circle. Two of the internal circles have half the radius of the large circle, and are, therefore, tangent to each other. The other two smaller circles are tangent to these circles. If a dart is thrown so that it sticks to a point randomly chosen on the dart board, then the probability that the dart sticks to a point in the shaded area is where m and n are relatively prime positive integers. Find m + n.

Problem 11

Six distinct positive integers are randomly chosen between 1 and 2011, inclusive. The probability that some pair of the six chosen integers has a difffference that is a multiple of 5 is n percent. Find n.

Problem 12

Find the area of the region in the coordinate plane satisfying the three conditions

x ≤ 2y
y ≤ 2x
x + y ≤ 60.

Problem 13

A 3 by 3 determinant has three entries equal to 2, three entries equal to 5, and three entries equal to 8. Find the maximum possible value of the determinant.

Problem 14

The lengths of the three sides of a right triangle form a geometric sequence. The sine of the smallest of the angles in the triangle is where m, n, and k are integers, and k is not divisible by the square of any prime. Find m + n + k.

Problem 15

A pyramid has a base which is an equilateral triangle with side length 300 centimeters. The vertex of the pyramid is 100 centimeters above the center of the triangular base. A mouse starts at a corner of the base of the pyramid and walks up the edge of the pyramid toward the vertex at the top. When the mouse has walked a distance of 134 centimeters, how many centimeters above the base of the pyramid is the mouse?

Problem 16

Evaluate 1³ − 2³ + 3³ − 4³ + 5³ − · · · + 101³.

Problem 17

In how many distinguishable rearrangements of the letters ABCCDEEF does the A precede both C’s, the F appears between the 2 C’s, and the D appears after the F?

Problem 18

Let a be a positive real number such that 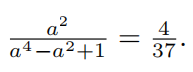Then where m and n are relatively prime positive integers. Find m + n.

Problem 19

The diagrams below shows a 2 by 2 grid made up of four 1 by 1 squares. Shown are two paths along the grid from the lower left corner to the upper right corner of the grid, one with length 4 and one with length 6. A path may not intersect itself by moving to a point where the path has already been. Find the sum of the lengths of all the paths from the lower left corner to the upper right corner of the grid.

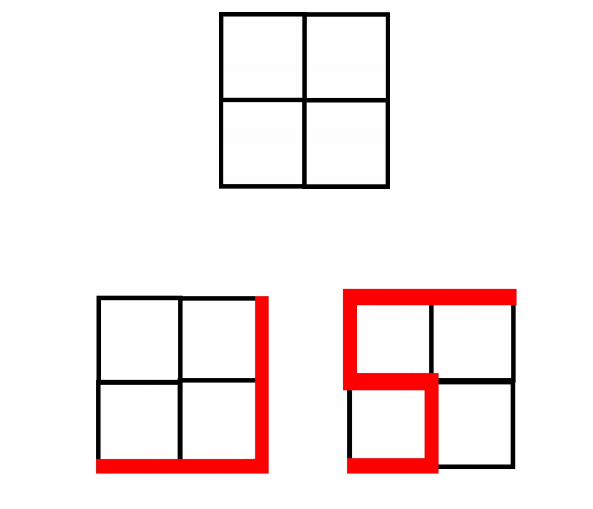
Problem 20

Points A and B are the endpoints of a diameter of a circle with center C. Points D and E lie on the same diameter so that C bisects segment Let F be a randomly chosen point within the circle. The probability that 4 DEF has a perimeter less than the length of the diameter of the circle is There are relatively prime positive integers m and n so that the ratio of DE to AB is . Find m + n.

Problem 21

If a, b, and c are non-negative real numbers satisfying a + b + c = 400, find the maximum possible value of

Problem 22

Five congruent circles have centers at the vertices of a regular pentagon so that each of the circles is tangent to its two neighbors. A sixth circle (shaded in the diagram below) congruent to the other fifive is placed tangent to two of the fifive. If this sixth circle is allowed to roll without slipping around the exterior of the fifigure formed by the other fifive circles, then it will turn through an angle of k degrees before it returns to its starting position. Find k.

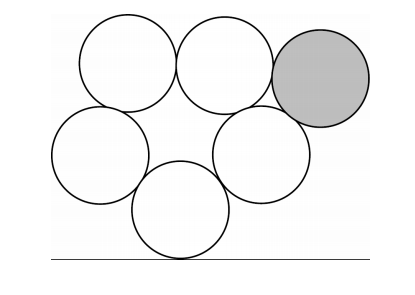
Problem 23

Let x be a real number in the interval such that

Evaluate

Problem 24

The diagram below shows a regular hexagon with an inscribed square where two sides of the square are parallel to two sides of the hexagon. There are positive integers m, n, and p such that the ratio of the area of the hexagon to the area of the square can be written as where m and p are relatively prime. Find m + n + p.

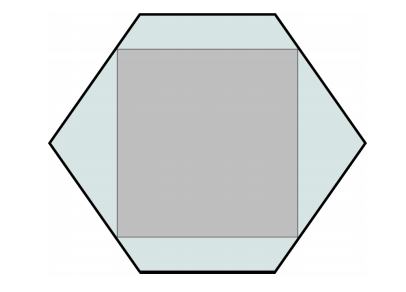
Problem 25

Find the remainder when A = 3³ · 33³³ · 333³³³ · 3333³³³³ is divided by 100.

Problem 26

The diagram below shows two parallel rows with seven points in the upper row and nine points in the lower row. The points in each row are spaced one unit apart, and the two rows are two units apart. How many trapezoids which are not parallelograms have vertices in this set of 16 points and have area of at least six square units?

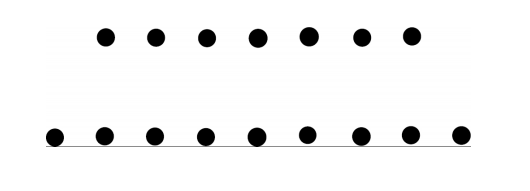
Problem 27

Find the smallest prime number that does not divide

9 + 9² + 9³ + · · · + 9²⁰¹⁰ .

Problem 28

Pictured below is part of a large circle with radius 30. There is a chain of three circles with radius 3, each internally tangent to the large circle and each tangent to its neighbors in the chain. There are two circles with radius 2 each tangent to two of the radius 3 circles. The distance between the centers of the two circles with radius 2 can be written as where a, b, c, and d are positive integers, c and d are relatively prime, and b is not divisible by the square of any prime. Find a + b + c + d.

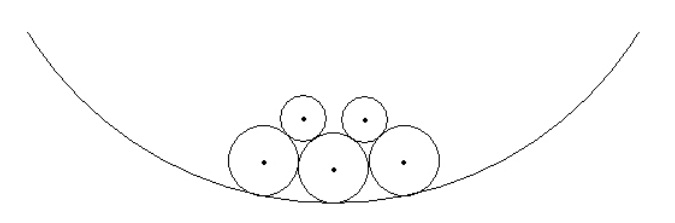
Problem 29

Let S be a randomly selected four-element subset of {1, 2, 3, 4, 5, 6, 7, 8}. Let m and n be relatively prime positive integers so that the expected value of the maximum element in S is . Find m + n.

7Problem 30

Four congruent spheres are stacked so that each is tangent to the other three. A larger sphere, R, contains the four congruent spheres so that all four are internally tangent to R. A smaller sphere, S, sits in the space between the four congruent spheres so that all four are externally tangent to S. The ratio of the surface area of R to the surface area of S can be written m + √n where m and n are positive integers. Find m + n.