- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
紫色彗星数学竞赛真题(2010年高中组)
PURPLE COMET MATH MEET April 2010
HIGH SCHOOL - PROBLEMS
Copyright Titu Andreescu and Jonathan Kane
Problem 1
Let x satisfy (6x + 7) + (8x + 9) = (10 + 11x) + (12 + 13x). There are relatively prime positive integers so
that x = −![]() . Find m + n.
. Find m + n.
Problem 2
The prime factorization of 12 = 2 · 2 · 3 has three prime factors. Find the number of prime factors in the factorization of 12! = 12 · 11 · 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1.
Problem 3
The grid below contains six rows with six points in each row. Points that are adjacent either horizontally or vertically are a distance two apart. Find the area of the irregularly shaped ten sided fifigure shown.
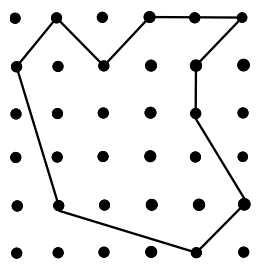
Problem 4
Sally’s salary in 2006 was $37,500. For 2007 she got a salary increase of x percent. For 2008 she got another salary increase of x percent. For 2009 she got a salary decrease of 2x percent. Her 2009 salary is $34,825. Suppose instead, Sally had gotten a 2x percent salary decrease for 2007, an x percent salary increase for 2008, and an x percent salary increase for 2009. What would her 2009 salary be then?
Problem 5
If a and b are positive integers such that a · b = 2400, fifind the least possible value of a + b.
Problem 6
Evaluate the sum 1 + 2 − 3 + 4 + 5 − 6 + 7 + 8 − 9 · · · + 208 + 209 − 210.
Problem 7
Find the sum of the digits in the decimal representation of the number 52010 · 16502 .
Problem 8
The diagram below shows some small squares each with area 3 enclosed inside a larger square. Squares that touch each other do so with the corner of one square coinciding with the midpoint of a side of the other square. Find integer n such that the area of the shaded region inside the larger square but outside the smaller squares is ![]()

Problem 9
Find positive integer n so that ![]() is the reciprocal of
is the reciprocal of 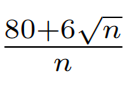 .
.
Problem 10
The set S contains nine numbers. The mean of the numbers in S is 202. The mean of the fifive smallest of the numbers in S is 100. The mean of the fifive largest numbers in S is 300. What is the median of the numbers in S?
Problem 11
A jar contains one white marble, two blue marbles, three red marbles, and four green marbles. If you select two of these marbles without replacement, the probability that both marbles will be the same color is ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 12
A good approximation of π is 3.14. Find the least positive integer d such that if the area of a circle with diameter d is calculated using the approximation 3.14, the error will exceed 1.
Problem 13
Let S be the set of all 10-term arithmetic progressions that include the numbers 4 and 10. For example, (−2, 1, 4, 7, 10, 13, 16, 19, 22, 25) and ![]() are both members of S. Find the sum of all values of a10 for each (a1, a2, a3, a4, a5, a6, a7, a8, a9, a10) ∈ S, that is,
are both members of S. Find the sum of all values of a10 for each (a1, a2, a3, a4, a5, a6, a7, a8, a9, a10) ∈ S, that is, 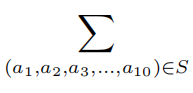 a10.
a10.
Problem 14
There are positive integers b and c such that the polynomial 2x2 + bx + c has two real roots which diffffer by 30. Find the least possible value of b + c.
Problem 15
Find the smallest possible sum a + b + c + d + e where a, b, c, d, and e are positive integers satisfying the conditions
- each of the pairs of integers (a, b), (b, c), (c, d), and (d, e) are not relatively prime
- all other pairs of the fifive integers are relatively prime.
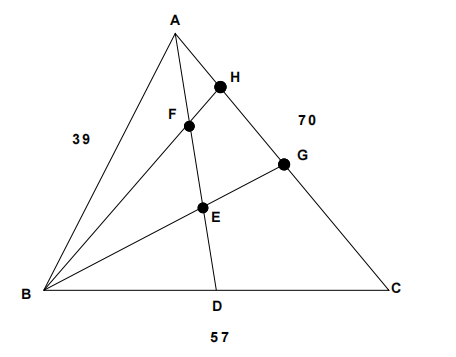
Problem 16
The triangle ABC has sides lengths AB = 39, BC = 57, and CA = 70 as shown. Median ![]() is divided into three congruent segments by points E and F. Lines BE and BF intersect side
is divided into three congruent segments by points E and F. Lines BE and BF intersect side ![]() at points G and H, respectively. Find the distance from G to H.
at points G and H, respectively. Find the distance from G to H.
Problem 17
Alan, Barb, Cory, and Doug are on the golf team; Doug, Emma, Fran, and Greg are on the swim team;
and Greg, Hope, Inga, and Alan are on the tennis team. These nine people sit in a circle in random order. The probability that no two people from the same team sit next to each other is ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 18
When 4 cos θ − 3 sin θ = ![]() , it follows that 7 cos 2θ − 24 sin 2θ =
, it follows that 7 cos 2θ − 24 sin 2θ = ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 19
The centers of the three circles A, B, and C are collinear with the center of circle B lying between the centers of circles A and C. Circles A and C are both externally tangent to circle B, and the three circles share a common tangent line. Given that circle A has radius 12 and circle B has radius 42, fifind the radius of circle C.
Problem 20
How many of the rearrangements of the digits 123456 have the property that for each digit, no more than two digits smaller than that digit appear to the right of that digit? For example, the rearrangement 315426 has this property because digits 1 and 2 are the only digits smaller than 3 which follow 3, digits 2 and 4 are the only digits smaller than 5 which follow 5, and digit 2 is the only digit smaller than 4 which follows 4.
Problem 21
Let a be the sum of the numbers:
99 × 0.9
999 × 0.9
9999 × 0.9
……
999 · · · 9 × 0.9
where the fifinal number in the list is 0.9 times a number written as a string of 101 digits all equal to 9. Find the sum of the digits in the number a.
Problem 22
Ten distinct points are placed in a circle. All ten of the points are paired so that the line segments connecting the pairs do not intersect. In how many difffferent ways can this pairing be done?
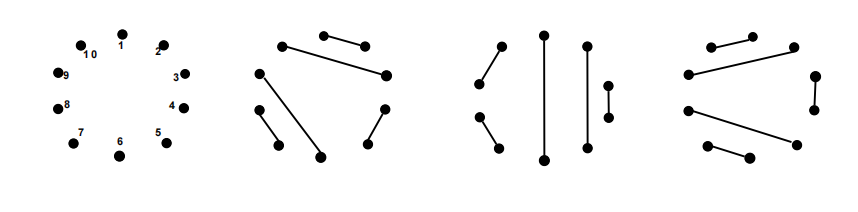
Problem 23
A disk with radius 10 and a disk with radius 8 are drawn so that the distance between their centers is 3. Two congruent small circles lie in the intersection of the two disks so that they are tangent to each other and to each of the larger circles as shown. The radii of the smaller circles are both ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
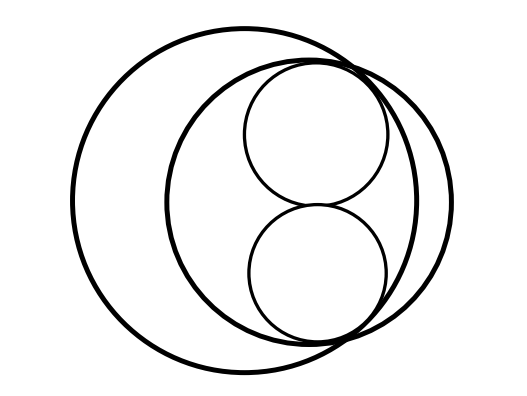
Problem 24
Find the number of ordered pairs of integers (m, n) that satisfy 20m − 10n = mn.
Problem 25
Let x1, x2, and x3 be the three roots of the polynomial x3 + 3x + 1. There are relatively prime positive
integers m and n so that ![]() Find m + n.
Find m + n.
Problem 26
In the coordinate plane a parabola passes through the points (7,6), (7,12), (18,19), and (18,48). The axis of symmetry of the parabola is a line with slope ![]() where r and s are relatively prime positive integers. Find r + s.
where r and s are relatively prime positive integers. Find r + s.
Problem 27
Let a and b be real numbers satisfying 2(sin a + cos a) sin b = 3 − cos b. Find 3 tan2 a + 4 tan2 b.
Problem 28
There are relatively prime positive integers p and q such that 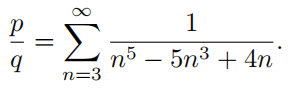 Find p + q.
Find p + q.
Problem 29
Square ABCD is shown in the diagram below. Points E, F, and G are on sides ![]()
respectively, so that lengths BE, BF, and DG are equal. Points H and I are the midpoints of segments
![]() respectively. Segment GJ is the perpendicular bisector of segment HI. The ratio of the areas of pentagon AEHJG and quadrilateral CIHF can be written as
respectively. Segment GJ is the perpendicular bisector of segment HI. The ratio of the areas of pentagon AEHJG and quadrilateral CIHF can be written as ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
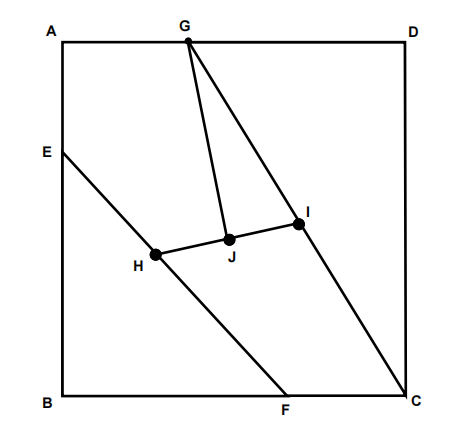
Problem 30
Let x and y be real numbers satisfying
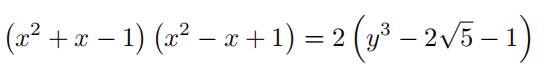
and
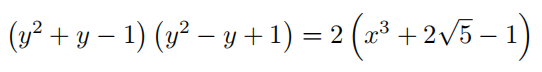
Find 8x2 + 4y3.
扫描下方二维码获取本年度学术活动答案及解析
还可免费领取最新年度真题及答案解析


最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









